HiDDEN：一种机器学习方法，用于检测病例对照单细胞转录组数据中的疾病相关人群

HiDDEN：一种在病例对照研究中揭示微妙转录异质性和扰动标记的计算方法

直觉

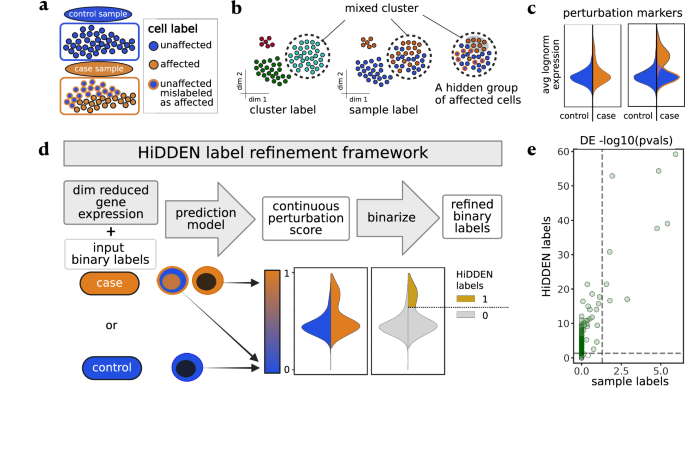
在病例对照实验中，通常对照样本中的所有细胞都不会受到影响，并且可能只有病例样本中的一部分细胞会受到扰动的影响（图 1）。 1a）。单独使用基因表达谱可能无法区分受影响的细胞和未受影响的细胞（图 1）。 1b）。单独使用样本级标签可能无法恢复扰动标记（图 1）。 1c）。然而，将两者结合起来使我们能够利用至少一些标签是正确的，并允许预测模型利用与正确标记的细胞相对应的特征中的共享变异性。因此，我们将样本级标签转换为细胞特定的扰动效应分数，并可以分配表示其受影响或不受影响状态的二进制细胞标签（图 1）。 1天）。我们利用这些信息来找到难以检测的受影响的细胞亚群，表征它们的标记基因，并将它们的细胞通讯模式与未受影响的细胞进行对比。

符号

让XÏμR^尼姆表示包含基因表达谱的矩阵\(N\)细胞横跨\(M\)基因。让ZÏμR^内克表示减少的表示\(N\)细胞在一个\(K\)特征的维度潜在空间。让\(Y{\epsilon }\{{\mathrm{0}},{\mathrm{1}}\}^{N}\)表示编码每个单元的样本级标签的二进制向量，其中\(0\)代表控制和\(1\)代表案例。我们训练一个预测模型，表示为\(h\左(.\右)\)关于减少代表性\(Z\)和二进制样本级标签\（是\）。由于病例对照标签的二元性质\（是\），预测模型是一个二元分类器，对标签的概率进行建模\(1\)给定输入特征，即\(P\左(Y=1,|,Z\右)=h\左(Z\右)\)。我们在感兴趣的数据集上训练分类器的参数并表示拟合值\(P\左(Y=1,|,Z\右)\)和\(\帽子{p}\)。最后，我们对连续分数进行聚类\(\帽子{p}\)导出精炼的二进制标签，表示为\(\widetilde{Y}\)，反映每个细胞受扰动影响或未影响的状态，无论其源自哪个样本。

潜在空间的构建

我们改造\(N\乘以M\)基因表达矩阵\(X\)进入一个\(N\乘以K\)矩阵\(Z\)包含数据集中每个细胞的基因表达谱的信息丰富的简化表示。在这项工作中对真实数据的应用中，我们使用主成分分析 (PCA) 来完成这项任务，这是单细胞 RNA-seq 数据常用的降维技术。原则上，任何其他信息保留降维方法都可以用来构建潜在特征来代替 PCA，例如非负矩阵分解（NMF），或者来自最先进的单特征向量的潜在表示。细胞表达自动编码器¹¹。我们没有找到令人信服的证据表明使用更复杂的降维技术可以提高模型性能（补充图1） 5），因此采用 PCA 作为计算效率最高的选项。

连续扰动分数的估计

对于每个单元格，我们得出一个连续分数，\(\hat{p}{\rm{\epsilon }}\left[\mathrm{0,1}\right]\)，反映了该细胞相对于数据集中其他细胞的扰动效应的强度。在整个工作中，我们使用逻辑回归来完成这项任务。即标签的预测概率\(1\)给定输入特征由下式给出

在哪里\(h\)是 logit 链接函数，即\（克\）是逻辑函数，并且\(\帽子{\测试版}\)是\(K\)拟合回归参数的维向量。原则上，我们可以使用任何分类器\(h:{R}^{N\times K}\到{\left[\mathrm{0,1}\right]}^{N}\)，包括大参数非线性模型，例如神经网络。在实践中，我们选择逻辑回归作为一种简单但功能强大的模型，具有规范参数优化例程，不会引入额外的超参数、训练启发式方法以及增加的计算资源和时间需求。

精炼二元标签的推导

病例对照实验数据集中的每个细胞都拥有一个二元样本级别标签，反映它是源自病例样本还是对照样本。由于这些粗略标签不能反映受扰动影响或未受影响的单个细胞身份，因此我们得出了一个新的精炼二元标签，可以捕获每个细胞中是否存在扰动效应。当我们想要区分案例样本中受影响和未受影响的细胞时，我们对连续扰动分数进行聚类\(\帽子{p}\)对于所有带有初始标签的单元格\(1\)分成两组。较低组中的细胞\(\帽子{p}\)分数获得新标签\(\widetilde{Y}=0\)以及具有较高组中的细胞\(\帽子{p}\)分数获得新标签\(\widetilde{Y}=1\)与他们的旧标签相匹配。为此，我们使用 k 均值聚类\(k=2\)。原则上，任何其他聚类算法（例如具有两个分量的高斯混合模型）都可以用来代替 k 均值。我们在真实的 Naive B / Memory B 混合物中比较了这两种聚类方法，并得出结论，这两种聚类策略往往表现相似，特别是对于具有\(15\%\)到\(75\%\)案例条件下的记忆B细胞。对于小于\(15\%\)记忆 B 细胞、高斯混合模型方法总体上更有能力检测真实标记基因。然而，对于超过\(75\%\)在记忆 B 细胞的情况下，k 均值表现更好，特别是由于错误发现率较低。

选择潜在维度的数量

选择时\(K\)，潜在维度的数量，我们的指导原则是\(K\)应以数据依赖的方式选择，旨在保留信息转录异质性，同时避免过度拟合不完全正确的样本水平标签。例如，请注意使用\(K > {\rm{等级}}(X)\)将产生预测\(\帽子{p}\)与样本级标签同义。在实践中，这意味着我们应该选择\(K < < \min (N,M)\)。因此，我们开发了两种新颖的数据驱动启发式方法，通过测量重新定义二进制标签下游的扰动信号来量化潜在空间中保留的信息异质性量。

第一个启发式是使用由精炼标签定义的差异表达基因的数量\(\widetilde{Y}\)。大量的DE基因表明了有意义的信号\(\widetilde{Y}\)，依次在\(\帽子{p}\)和潜在空间\(Z\)。直观地讲，当\(K\)太小，连续分数\(\帽子{p}\)不包含足够的异质性来产生标签\(\widetilde{Y}\)区分DE基因。相反，当\(K\)太大，我们过度拟合样本级标签，导致检测扰动标记的能力较低。为了达到适当的平衡，我们扫描一系列值\(K\)遍历之间的凹关系\(K\)和 DE 基因的数量，并选择最大化它的潜在维度的数量。

第二个启发式是利用值之间差异的强度\(\帽子{p}\)对于带有新标签的病例样本中的细胞\(\widetilde{Y}=1\)和新标签\(\widetilde{Y}=0\)。我们使用双样本 Kolmogorov-Smirnov (KS) 检验量化这两组值从同一分布中得出的概率³²。KS 检验统计量的值越大，预测受影响的细胞和未受影响的细胞之间的扰动分数的样本分布差异越大。该值通常是以下函数的增函数\(K\)，因此我们选择最小值\(K\)最大化 KS 检验统计量。

请注意，我们不需要访问这两种启发式的扰动效应的真实标签。当地面实况数据可用时，我们发现精炼的二进制标签的能力\(\widetilde{Y}\)表示每个细胞的真实扰动效应对于各种值来说同样高\(K\)并且任一启发式都会在该范围内产生选择（补充图。 9）。

评估半模拟地面实况数据的性能

为了演示和量化问题难度并评估我们方法的功效，我们使用真实的单细胞数据集进行了模拟。我们使用的 RNA 谱\(n=1900\)天真的B和\(n=1630\)来自 10x Genomics 免费提供的外周血单核细胞 (PBMC) 数据集的记忆 B 细胞¹⁶。我们首先通过结合两个 B 细胞亚群来描述我们的模拟病例对照数据集的设计。然后，我们描述了使用标准单细胞聚类分析工作流程分离两个亚群的挑战。最后，我们描述了如何训练我们的方法以及我们用来评估其检测生物信号的能力并将其与相关方法进行比较的指标。

地面实况数据集的生成

所有的 RNA 谱\(n=30672\)来自 10x Genomics 的人类 PBMC 数据中的细胞按照 Seurat 加权最近邻分析小插图中详述的标准方法进行独立于 ATAC-seq 配置文件的聚类和注释³³。这导致了\(27\)带注释的细胞类型，我们将所有 Naive B 和 Memory B 细胞进行子集化，以用于后续生成地面实况数据集。

对于图 1 中所有 Naive B 和所有 Memory B 细胞的 tSNE 表示 2a，我们标准化基因计数，执行可变基因选择，缩放标准化计数，使用 PCA 执行降维，构建最近邻图，并运行 tSNE，所有这些都使用 Seurat v 3.2.3 中的标准函数使用默认超参数值²⁶。

为了全面描述问题难度并测试我们方法的性能，我们通过改变两个方面构建了一组地面真实病例对照数据集（图 1）。 2b）。在每个数据集中，对照样本完全由朴素 B 细胞组成，我们将其称为未受扰动的细胞，而病例数据集由未受扰动的细胞和受扰动的细胞组成，它们是记忆 B 细胞或朴素 B 细胞和记忆 B 细胞的细胞。每个数据集均按 (1) 案例样本中受扰动细胞的百分比和 (2) 扰动强度进行索引。

为了探讨案例样本中受干扰细胞百分比的影响，我们随机抽取了\(\左(100-p\右)\%\)病例中的细胞来自初始 B 细胞和\(p\%\)来自记忆B细胞。剩余的 Naive B 细胞全部分配给对照样本。我们探索了\(18\)扰动细胞的百分比值\(p{\rm{\epsilon }}\{\mathrm{5,10,15},\ldots,\mathrm{85,90}\}\%.\)补充表中提供了每个数据集的病例和对照中朴素 B 和记忆 B 细胞的最终数量 1。

为了探索扰动强度的影响，我们改变了案例样本中受扰动和未受扰动细胞之间的差异程度。让\({W}^{\左(米\右)}\)和\({W}^{\左(n\右)}\)分别表示每个混合单元的记忆 B 和朴素 B 贡献的权重，其中\({W}^{\left(m\right)}+{W}^{\left(n\right)}=1\)， 和\({W}^{\左(米\右)},{W}^{\左(米\右)}\ge 0\)， IE。\({W}^{\左(米\右)}\)表示扰动的强度。让\（我\）对案例样本中受到干扰的（记忆 B）细胞进行索引，并让\({N}_{i}\)表示单元格中 UMI 的总数\（我\）。每个Memory B / Naive B混合单元具有相同数量的UMI，\({N}_{i}\)，作为它起源的记忆 B 细胞，\({N}_{i}^{\左(m\右)}\)其中是从原始记忆 B 细胞中二次采样的\({N}_{i}^{\left(n\right)}\)其中是从 Naive B 质心轮廓中绘制的，如下所述。

让\(\vec{{x}_{i}}\)表示原始记忆 B 细胞的基因表达谱\（我\）。让\(\vec{{p}_{i}}\)表示标准化计数，即跨基因计数的相对比例。我们绘制了 Memory B / Naive B 混合基因表达谱\(\vec{{h}_{i}}\)通过第一次子采样\({N}_{i}^{\left(m\right)}=\text{天花板}\left({W}^{\left(m\right)}*{N}_{i}\正确的）\）从原始记忆 B 表达谱中计数\(\overrightarrow{{x}_{i}}\):

其中任何实数的上限函数\(x\), 整数\(z\)，以及整数集\({\mathbb{Z}}\)被定义为上限\((x)={\rm{min}} \{z{\epsilon }{\mathbb{Z}}| z \ge x \}\)，即上限是大于或等于 x 的最小整数；和\({\rm{多项式}}\)表示多项式概率分布。

然后我们画了\({N}_{i}^{\left(n\right)}:={N}_{i}-{N}_{i}^{\left(m\right)}\)从 Naive B 质心开始计数，\(\overrightarrow{{p}^{\left(n\right)}}\)，定义为数据集中所有 Naive B 细胞的平均归一化计数 overrightarrowtor：

最后，总结了两个计数 overrightarrowtors\(\overrightarrow{{h}_{i}}=\overrightarrow{{h}_{i}^{\left(m\right)}}+\overrightarrow{{h}_{i}^{\left(n\右)}}\)组成混合配置文件。

我们探索了\(17\)扰动强度参数值\({W}^{\left(m\right)}{\rm{\epsilon }}\{\mathrm{0.25,0.3,0.35},\ldots,\mathrm{0.95,1}\}\)。总的来说，跨越案例中扰动细胞的百分比和扰动强度轴，我们生成了\(72\)数据集来表征问题难度并评估我们方法的性能，如下所述。

地面真实数据集的聚类分析

对于图 1 中的 tSNE 表示 2c，我们重点关注案例中包含 5% 记忆 B 细胞的模拟数据集。我们使用标准 Seurat 函数并对基因计数进行归一化，使用默认参数值执行可变基因选择，缩放归一化计数，使用默认参数值使用 PCA 执行降维，使用默认最近邻数构建最近邻图，使用带有分辨率参数默认值的 Leiden 算法来查找簇，并运行 tSNE。对于图中的条形图 2d和补充图。 1，我们计算了每个簇中病例和对照标记细胞的丰度以及幼稚 B 和记忆 B 细胞的丰度。

几个超参数会影响聚类结果，我们改变每一个超参数来研究它们对问题难度的影响。使用标准流程捕获生物信号并从 Naive B 细胞中分离 Memory B 的挑战在于（1）潜在空间的构建；(2)聚类算法的分辨率参数。为了量化问题的难度，我们通过记忆 B 细胞最近邻的数量分布，研究了潜在空间中朴素 B 细胞和记忆 B 细胞的可分离程度。对于给定的模拟数据集，改变用于构建最近邻图的主成分 (PC) 的数量会影响潜在空间的可分离性，因为包含更多的 PC 会导致更加混合的潜在空间（补充图 1）。 1a）。特征选择策略的选择以及莱顿聚类算法分辨率参数的选择对结果有显着影响。我们观察到，使用高度可变的基因选择和选择的分辨率参数来产生两个簇（因为我们的目标是分离两种细胞类型）无法分离记忆 B 细胞（补充图 1）。 1b）。在这个模拟的真实设置中，我们可以计算两个类之间的差异表达（DE）基因，即标记基因，并将它们用作所选特征。然而，当使用分辨率参数的默认值时，单独的选择也不足以产生改进的聚类（补充图 1）。 1c）。

HiDDEN模型训练

HiDDEN 模型训练是在 python 中完成的，由三个步骤组成：(1) 我们预处理原始基因表达计数，(2) 训练逻辑回归模型，(3) 我们对案例样本中的细胞预测进行二值化。首先，我们遵循 scanpy 中单细胞 RNA-seq 数据的标准预处理例程²⁶其中包括过滤掉细胞\( < 20\)基因并过滤掉在任何细胞中不表达的基因，然后进行对数归一化，然后，我们在缩放后的基因特征上使用 scanpy 中的标准 PCA 降维例程。补充图中降维技术选择的比较 5，我们使用 scVI 框架训练了最先进的基因表达自动编码器¹¹，改变潜在空间的大小\(K{\rm{\epsilon }}\{\mathrm{10,25,50}\}\)。其次，我们使用 sklearn.linear_model python 库中的 LogisticRegression 函数来训练二元样本级别标签和第一个标签上的逻辑回归\(K\)特征。最后，我们使用了 sklearn.cluster python 库中的 KMeans 函数\({\rm{n}}\_{\rm{簇}}=2\)案例样本中细胞的逻辑回归输出的连续扰动分数。

请注意，HiDDEN 不需要参数调整。由于我们在计算数据的 PC 嵌入时使用所有基因，因此模型中的唯一参数是\(K\)，用于逻辑回归训练的 PC 数量。如本节前面所述，我们提供了两种数据驱动的启发式方法，用于自动选择适当的值\(K\)。对于每个数据集和每个启发式，我们扫描了所有整数值\(K\)在范围内\([\mathrm{2,60}]\)。第一个启发式是选择\(K\)最大化由 HiDDEN 精炼二元标签定义的 DE 基因的数量。计算给定值下游的 DE 基因数量\(K{\rm{\epsilon }}[\mathrm{2,60}]\)，我们在 scanpy 中使用了 Wilcoxon 秩和差异表达测试，并进行了调整p-值阈值\( < 0.05\)（补充图 9a）。第二个启发式是选择最小的值\(K\)最大化两个样本 Kolmogorov-Smirnov (KS) 检验统计量的值，比较样本分布\(\帽子{p}\)适用于带有新精制标签的病例样本中的细胞\(\widetilde{Y}=1\)和\(\widetilde{Y}=0\)（补充图 9b）。为了计算 KS 检验统计量的值，我们使用了 scipy.stats python 库中的 ks_2samp 函数。

评估 HiDDEN 连续扰动分数和地面真实标签之间的一致性

为了量化 HiDDEN 输出的连续扰动分数的能力，以捕获每个模拟数据集中记忆 B 细胞和幼稚 B 细胞之间的生物学差异，我们使用 sklearn 中的 roc_auc_score 函数计算了接受者操作特征曲线下的面积 (AUROC)。指标 python 库（图 1） 2f，补充图。 2a,5a,6a,7I-K）。AUROC 分数可以取以下范围内的值\([\mathrm{0,1}]\)，值越高表示连续预测分数与真实的 Naive B / Memory B 二进制标签之间的一致性越好。

评估 HiDDEN 精炼的二进制标签和真实标签之间的一致性

为了评估每个模拟数据集中的真实 Naive B / Memory B 标签与 HiDDEN 精炼的二进制标签之间的一致性，我们测量了检索到的真实标记的准确性。在这里，我们考虑了两种场景 - (1) 将（非聚类）数据集作为一个整体进行处理，以及 (2) 在标准 Seurat 工作流程生成的聚类中寻找扰动标记。

非聚类情况：为了定义每个模拟数据集中朴素 B 和记忆 B 细胞的地面实况标记集，我们使用 Scanpy 中的 Wilcoxon 秩和差异表达测试，使用朴素 B/记忆 B 地面实况标签计算 DE 基因经调整p-值阈值\( < 0.05\)。类似地，我们在相同的测试程序下分别使用精炼的二元标签和样本级病例对照标签定义了一组 HiDDEN 衍生的标记基因以及一组基线标记基因。然后，我们计算了真阳性 (TP)、假阴性 (FN)、假阳性 (FP) 的数量以及召回率、精确度和 F1 分数的相关指标（图 1）。 2克，补充图。 2b,3,4a,5b,6b）。召回率可以取范围内的值\([\mathrm{0,1}]\)，值越高表示正确检索的地面实况标记的比例越高。精度可以取范围内的值\([\mathrm{0,1}]\)，值越低表明错误发现的标记基因的比例越高。F1 分数计算为精度和召回率的调和平均值。F1-score 可以取范围内的值\([\mathrm{0,1}]\)，值越高表示 HiDDEN 精炼二进制标签与地面实况 Naive B / Memory B 二进制标签之间的一致性越好。

聚类情况：我们与非聚类情况类似，不同之处在于每个聚类都进行 DE 测试，并且跨聚类的所有 DE 基因的联合定义了最终的基因集（补充图 1）。 3）。

HiDDEN 与 CNA、MELD、Milo 和 Mixscape 的比较

虽然这些方法是在表征单细胞数据扰动影响的更大问题中出于不同的目标而开发的，但所有这些方法都利用表达谱（或从中派生的邻域图）和反映样本条件的细胞标签cell 来自（以及其他元数据，可选）作为输入。所有方法都会输出一个连续的分数，测量每个细胞中扰动的影响，可以在适当的时候进一步二值化。因此，我们可以根据连续分数和二进制标签来比较这五种方法的性能。为此，我们使用 Naive B 和 Memory B 细胞混合物的真实数据集。

CNA 的训练是按照该方法作者提供的 jupyter Notebook 教程在 python 中进行的³⁴。最初的 CNA 实现有一个硬编码的假设，即要分析的数据集至少由五个样本组成。我们放宽了这一假设以适应我们的 B 细胞混合物，并使用 CNA 关联函数获得连续扰动分数作为每细胞邻域系数，其中病例/对照状态作为感兴趣的样本级属性，病例/对照状态作为样本 ID。生成的 CNA 连续分数是范围从 1 到 1 的相关值。

MELD 的训练是按照 Milo 作者在比较部分中使用的代码在 python 中完成的³⁵。我们根据前 2000 个高度可变基因的表达矩阵计算了 k 最近邻图。然后，我们使用 meld_op.transform 函数来计算病例/对照样本标签的密度，并使用 meld.utils.normalize_densities 函数将密度转换为每个条件的可能性。连续扰动分数（取值在 0 和 1 之间）作为标签 1 的可能性获得，该标签表示情况条件。

Milo 的训练是按照该方法的作者提供的使用 milopy jupyter 笔记本教程在 python 中进行差异丰度分析进行的³⁶。Milo 的底层实现是在 R 中完成的，并调用 EdgeR R 包中的 glmFit 例程。如果未给出至少三个样本，则此例程无法估计负二项式色散参数。为了克服这种硬编码的假设，我们为每个条件随机创建了三个样本。我们使用 milo.make_nhoods 函数创建了部分重叠的细胞邻域。这会产生一个邻域集合，每个邻域都由一个索引单元格标识。数据集中的一小部分细胞被故意从 Milo 分析中作为异常值排除。分析中包含的像元也可以同时属于一个或多个邻域。然后，我们使用 milo.count_nhoods 函数，使用病例/对照样本级别标签来计算每个邻域中每个样本的细胞数量。我们使用 milo.DA_nhoods 函数执行差异丰度测试，输出每个邻域的对数倍数变化测试统计量。由于我们的目标是在单个细胞水平上进行比较，因此当一个细胞属于多个邻域时，我们报告了邻域之间的平均对数倍数变化。对于从分析中排除的细胞，平均对数倍数变化为 NA。连续扰动分数以平均对数倍数变化的形式获得，并且可以取负无穷大到正无穷大之间的值。

Mixscape 的训练是按照 Theis 实验室提供的代码（作为 github 上 pertpy 工具的一部分）在 python 中进行的https://github.com/theislab/pertpy/blob/development/pertpy/tools/_mixscape.py。我们通过使用 perturbation_signature 函数从每个细胞的表达谱中减去 20 个对照邻居的平均表达谱来计算扰动特征。然后，我们使用 mixscape 函数和默认超参数值来识别案例条件下的扰动和非扰动单元。

HiDDEN、CNA、MELD、Milo 和 Mixscape 的连续扰动分数的比较（补充图 1） 6a,7）是使用方法部分前面描述的 AUROC 作为评估连续扰动分数和真实标签之间一致性的指标来执行的。

对于 HiDDEN、CNA、MELD 和 Milo，以相同的方式将连续扰动分数转换为二值化标签，如方法部分前面所述。Mixscape 有一个内置函数，用于计算二进制扰动/非扰动标签。所有五种方法的二进制标签的比较（补充图。 6b,8）是使用方法部分前面描述的 F1 分数作为评估 HiDDEN 精炼的二进制标签和真实标签之间一致性的指标来执行的。

使用 HiDDEN 精炼的二进制标签作为 CNA、MELD 和 Milo 的输入

与样本级案例/对照标签相比，HiDDEN 精炼的二进制标签与真实标签表现出更好的一致性。因此，我们探索了当给出 HiDDEN 二进制标签代替案例/控制标签作为输入时 CNA、MELD 和 Milo 的性能（补充图 1）。 7,8）。使用 CNA 关联函数，以 Memory B / Naive B 真实标签作为感兴趣的样本级属性，以 HiDDEN 精炼的二进制标签作为样本 id，获得 CNA 连续扰动分数作为每单元邻域系数。MELD 连续扰动分数是通过将 HiDDEN 精炼二元标签的密度转换为标签 1 的可能性而获得的。Milo 连续扰动分数是通过使用 HiDDEN 精炼二元标签对每个邻域进行差异丰度测试下游的平均对数倍数变化来获得的计算每个条件的单元格数量。所有连续分数均以与上述相同的方式二值化。

评估人类多发性骨髓瘤和前兆状态数据的表现

我们分析的第一个真实数据集包含来自多发性骨髓瘤 (MM) 患者的人骨髓浆细胞的单细胞 RNA-seq 谱（\(n=8\)患者，\(N=10790\)细胞），其先兆条件为闷烧型多发性骨髓瘤（SMM）（\(n=12\)患者，\(N=8431\)细胞）和意义未明的单克隆丙种球蛋白病（MGUS）（\(n=6\)患者，\(N=817\)细胞）和具有正常骨髓（NBM）的健康捐献者（\(n=9\)患者，\(N=9329\)细胞）⁴。

前体样本可能含有肿瘤细胞和正常细胞的混合物（图 1）。 3a）和原始研究的作者定义了描述前体样本及其细胞的恶性状态的两个基本事实来源。第一个来源是反映细胞是健康还是恶性的二进制标签的手动注释。第二个来源是每个前体样本中恶性细胞比例的肿瘤纯度估计。

HiDDEN模型训练

该数据集具有明显的患者特定批次效应（补充图 1） 12a）。因此，与原始研究中的分析相呼应，我们首先部署了批量敏感策略，使用 HiDDEN 细化前体样本中细胞的恶性状态。此外，我们还制定了一种批处理策略，以探索我们方法在存在强大批处理效应下表现良好的能力。在原始研究中反映了门内注释方法，我们的批敏感拟合方法一次都考虑了每个前体样本。我们在所有NBM，一个前体样品和所有MM样品上训练了该模型\（0 \）或健康，所有其余标签\（1 \），反映它们不是源于健康捐助者。批处理拟合方法包括将模型拟合到所有NBM样品，所有手动注释为混合的前体样品以及所有MM样品。除此之外，模型培训的所有其他方面都是在两种策略之间进行的。批处理特定策略的结果在图中列出了。 3，批处理方法的结果以及两者的比较都包括在补充图中。 12。

隐藏的模型培训是在Python进行的。首先，我们遵循SCANPY中单细胞RNA-seq数据的标准预处理程序，并分别对数符合每个样品进行对数均衡。然后，我们在缩放基因特征上使用了Scanpy中标准的PCA维度降低常规。接下来，我们使用sklearn.linear_model python库中的LogisticRecression函数来训练在二进制NBM / NON-NBM标签上的Logistic回归和第一个。\（k \）件。最后，我们使用了Sklearn.Cluster Python库中的Kmeans函数\（{\ rm {n}} \ _ {\ rm {clusters}} = 2 \）在连续的扰动上，分别通过每个前体样品中细胞的逻辑回归分数输出（补充表） 2）。我们使用所有基因来计算PC尺寸降低并自动选择\（k \），使用logistic回归中使用的PC数量，使用启发式方法来最大化隐藏精制二进制标签下游的DE基因数量（补充图。 13）。下面详细描述了以强批量影响为特征的该数据集中定义DE基因的特定策略。

在这两种拟合策略下，我们使用相同的下游指标来评估我们在恢复手动注释的细胞级标签和纯度样品级估计的方法的性能，如下所述。

评估隐藏的连续扰动分数与地面真相之间的一致性手动注释标签

为了量化隐藏在所有混合前体样品中捕获手动注释的健康型二进制标签所产生的连续扰动评分的能力，我们使用Sklearn.metrics Python python库中的ROC_AUC_SCORE函数计算了AUROC。图中描述了从批处理敏感训练策略中每个前体状态的平均AUROC。 3b，以及扰动评分的每样本曲线和分布。 12。

评估隐藏的精制二进制标签与肿瘤纯度样本估计之间的一致性

原始研究中提供的地面真理的样本级别来源是仅基于免疫球蛋白轻链基因表达的贝叶斯分层模型的恶性细胞比例的估计。此外，我们使用手动标签和隐藏的二进制标签估算了按样本肿瘤纯度估计。在所有三种情况下，置信度范围均与原始研究相同的方法得出（图 3c，e）。

与隐藏和手动注释标签概括样品纯度的地面真实点估计值的能力相关，即样品中的肿瘤细胞的比例：

1. 1.

   从隐藏的二进制标签中得出的样本纯度估计值，称为\（{p} _ {1} \）,

2. 2.

   基于手动注释的样品纯度的基于手动注释的估计值报道了数据起源于4表示为4\（{p} _ {2} \）,

3. 3.

   地面真相点的估计值估计恶性细胞的比例4，称为\（{p} _ {3} \）。

得出显着性值，以量化隐藏的标签和手动注释标签与恶性细胞比例的地面真相点估计值匹配的能力

我们对待\（{p} _ {1} \）和\（{p} _ {2} \）作为随机变量和点估计值\（{p} _ {3} \）作为标量。概率分布的\（{p} _ {1} \）和\（{p} _ {2} \）遵循原始研究中置信度界限的推导⁴并在下面更详细地描述。

对于给定的样本，让\（p \）是肿瘤细胞的比例（表示种群参数，而不仅仅是基于该样品的测序细胞的估计值）。我们将观察到的数据建模为

在哪里\（n \）表示样品中测序细胞的总数，\（x \）其中标记为肿瘤。我们在\（p \）:

由于β-二项式共轭性，后部分布\（p \）是封闭的表格：

和\（p \）占据价值\（[\ mathrm {0,1}] \）。

对于我们在图2中考虑的11个前体样本中的每个样本中的每一个 3c，e，我们检验了一对假设：

和

由于我们正在测试类似的假设\（{p} _ {1} \）和\（{p} _ {2} \），下面我们描述了有关的假设检验\（{p} _ {1} \）。

测试统计量的分布（之间的差异\（{p} _ {1} \）和\（{p} _ {3} \））在零假设下是：

有支持\（[ - {p} _ {3}，1- {p} _ {3}] \）\）， 在哪里\（{x} _ {3} \）是零下预期的肿瘤细胞数量，计算为\（{p} _ {3}*n \）四舍五入到最近的整数。

因此，p - 计算值是根据零分布观察到等于或更极端（远离0方向）的测试统计量的概率：

由此产生的p - 测试值\（{p} _ {1} - {p} _ {3} \）和\（{p} _ {2} - {p} _ {3} \）在所有11个混合前体样品中，均在补充表中报告 2。图中描述的意义 3c，e是关于alpha = 0.01/22 = 4.55e-04的Bonferroni调整后的阈值。较小的p - 值表示与地面真相的差异更大。每当隐藏的方法产生更大的方法p - 与手动注释相比，我们得出的结论是，与手动注释方法相比，隐藏与地面真理更好。使用手动注释和隐藏二进制标签的差分表达分析

为了证明隐藏精制的二进制标签从前体样本中发现其他恶性标记的能力，我们使用NBM和MM样品中的手动注释计算了DE基因，并将其与使用Pressor样品中隐藏精制标签发现的DE基因进行了对比

（图 3d）。由于数据中存在强大的批处理效应，因此反映了原始论文中的DE测试策略，因此我们发现了每个患者的DE基因并跨患者进行联合。为了将基因视为DE，必须进行调整p-价值\（<0.05 \）从scanpy中的t检验差分表达式测试常规和最大绝对log-foldchange\（> 1.5 \）。为了评估两组DE基因之间的重叠的重要性，我们使用统计r套件的dhyper函数进行了超几何测试。

基因的背景数是根据所有前体样品中至少一个细胞中表达的基因计算的（\（\ Mathrm {18,770} \）基因）。

在非混合MGUS样品中验证隐藏的二进制标签

原始研究的作者计算了贝叶斯非负基质分解（NMF），以突出该患者队列中活跃并在外部队列中验证它们的基因特征。用生物学解释注释了几个签名。根据手动注释，有三个被认为仅由健康细胞组成的MGU样品。它们也是根据原始研究的贝叶斯纯度模型最低但最低（尽管不是零）估计样品纯度的三个前体样品。这些患者的隐藏精制二进制标签注释了一些细胞为恶性肿瘤。为了验证这种注释，我们绘制了原始研究鉴定的基因的平均活性，用于标记为每个样品的细胞中的每个特征和恶性的细胞（图） 3f，补充图 11）。图中的置信度界限（SEM） 3f遵循与原始研究相同的方法得出的。

分析来自时间课的脱髓鞘实验的小鼠内皮细胞

产生脱髓鞘和控制组织

分析的第二个实际数据集由带有匹配的对照的脱髓鞘模型的小鼠内皮细胞的单核RNA-seq谱图组成。病例和对照动物分别接受500 nl的1％溶血磷脂酰胆碱（LPC，CAT＃440154，Millipore Sigma，US）或盐水载体（PBS）注射。使用标准方法在颅内交付，并在以下立体定位坐标中将纳米对象III（Drummond，US）传递到call体中：前后 - 后者：1.2。和1.4 mm的深度归一化为头骨表面。

所有小鼠均在68°F和79°F和30-70％湿度之间的12小时光/黑暗周期中固定在12小时的光周期中。所有动物工作均由Broad的机构动物护理和使用委员会（IACUC）批准。唯一使用的鼠标应变是直接从杰克逊实验室（CAT＃000664）购买的C57BL/6 j。在注射后3、7、12和18天以四个时间点处死小鼠（DPI）\（n = 3 \）每个条件的动物，总计\（n = 24 \）动物（图 4a）。在适当的时间点，将小鼠灌注冰冷的pH 7.4 HEPES缓冲液（含110毫米NaCl，10毫米HEPES，25毫米葡萄糖，75毫米蔗糖，75毫米蔗糖，7.5 mm MGCL2，MM MMGCL2，和2.5毫米KCl）去除大脑的血液。将大脑在液氮蒸气中新鲜冷冻3分钟，所有组织都存储在80°C以进行长期储存。完整的数据集将在即将发表的论文中描述（Dolan等人，在准备中）。

产生单核RNA轮廓

将冷冻的小鼠大脑安装在低温恒温器上，将OCT嵌入化合物在低温恒温器中。将大脑切开直到到达注射部位位置，通过使用NISSL染色（Histogene染色溶液，KIT0415，Thermofisher）的高细胞性存在证实。对于盐水控制，使用解剖学地标确定注射部位。使用1毫米活检打孔（Integra Miletex，US）对病变或对照白质进行了微解剖，其圆形打孔弯曲成无菌止血的矩形形状。病变打孔为300¼m深的。

使用预冷的镊子将每个切除的组织打孔放入预冷的0.25 ml PCR管中，并在80°C下储存最多24小时。根据方案可用的方案，使用温和的，基于洗涤剂的解离从该冷冻组织中提取细胞核。https://doi.org/10.17504/protocols.io.bck6iuze）较小的变化以最大化核提取，这将在即将到来的纸张中描述（Dolan等人的制备中）。将核加载到10倍铬V3系统中。逆转录和图书馆的产生是根据制造商的协议（10倍基因组学）进行的。使用带有默认设置的CellRanger v3.0.2对鼠标小脑实验的测序读数进行反复列出，并与鼠标（MM10）PremRNA参考对齐。使用细胞旋转器计数函数生成数字基因表达矩阵。总体UMAP和聚类的初始分析和生成（图 4b用Seurat V3进行²⁶。

内皮细胞的聚类分析

对于图中的UMAP表示 4C，d和补充图。 14概况\（n = 891 \）内皮细胞来自\（n = 6 \）跨越案例和控制条件以及所有四个时间点的动物，我们使用标准的扫描函数来对数正广度和缩放基因计数，ran pca，计算了最近的邻居图，并用\（10 \）第一个定义的潜在空间中的邻居\（50 \）PC并运行UMAP算法。

聚集内皮细胞（图 4天），我们在Seurat中使用了标准的预处理和聚类工作流程。我们对基因计数进行了归一化，用默认参数值执行了可变基因选择，缩放了归一化计数，使用具有默认参数值的PCA进行了降低尺寸，并使用默认的邻居数，并使用Leiden algorithm，并将其构建分辨率参数\（= 0.5 \）找到集群。

对于图中的热图 4e和补充图 14c，我们分别计算了每个群集和跨时间点中的情况（LPC）和对照（PBS）标签。

隐藏的模型培训

所有模型培训均在Python上进行\（n = 891 \）内皮细胞一起。我们遵循了Scanpy中单细胞RNA-Seq数据的标准预处理程序，并遵循对数符合基因计数的标准预处理，然后是缩放基因特征的PCA维度降低。对于图中的连续扰动评分。 4f和补充图 14天，我们使用Sklearn.linear_model Python库中的LogisticRecression函数来训练二进制PBS / LPC标签上的Logistic回归，而第一个。\（k \）件。我们使用所有基因计算PC嵌入并自动选择\（k = 5 \），在逻辑回归中使用的PC数量，使用启发式方法来最大化隐藏精制二进制标签下游的DE基因数量。下面详细描述了该数据集中定义DE基因的策略。

对于图。 4克，我们使用Sklearn.Cluster Python库中的Kmeans函数\（{\ rm {n}} \ _ {\ rm {clusters}} = 2 \）将所有LPC内皮细胞的连续扰动得分分为3 dpi。我们表示该组具有较低的扰动评分LPC0，对应于不受LPC注入影响的内皮细胞，类似于PBS控制条件中的内皮细胞，而具有较高扰动得分LPC1的组为受LPC注入的子集的扰动分数LPC1。。

定义内皮LPC1标记的差分表达分析

为了定义图中的点图中描绘的一组内皮LPC1标记。 5a，我们采用了使用隐藏的精制标签在DE分析中发现的独特的富含摄动的基因，而不是使用原始PBS / LPC标签在DE分析中。我们使用scanpy中的Wilcoxon Rank-sum测试进行了两项DE分析，并具有调整后的阈值p-价值\（<0.05 \）。两种测试的全面输出都可以在补充表中找到 3，发现使用隐藏的精制二进制标签发现的独特基因以粗体字体突出显示。

使用rnascope验证内皮LPC1标记

Fresh Frozen，14¼m注射后3天（DPI）脱髓鞘或盐水控制组织的切片安装在冷冻和幻灯片上（美国Fisher Scientific，美国）。这些幻灯片存储在80°C。我们使用针对的探针进行了Rnascope多重荧光V2（Advanced Cell Diagnostics，US）S100A6（412981），LGALS1（897151-C2）和FLT1（415541-C3），其中FLT1是内皮细胞的一般标记。按照制造商的新鲜冷冻组织的规程进行了rnascope，以1/1500的浓度使用以下染料来标记特定的mRNA（TSA Plus荧光素，TSA，TSA Plus Cyanine 3，TSA 3，TSA Plus Cyanine Plus Cyanine 5来自Perkinelmer，USA）。成像是在Andor CSU-X旋转磁盘共聚焦系统上进行的，该系统耦合到配备Andor Ikon-M相机的Nikon Eclipse Ti显微镜。使用20倍空气和60倍的油浸入目标（Nikon）获取图像。图中所示的所有图像 5b是从至少2个独立实验中拍摄的代表性图像。

使用基因本学分析对内皮LPC1标记的解释

为了鉴定基因本体论（GO）类别，总结了独特的内皮LPC1标记列表（图。 5c，d），我们在G：Profiler中进行了GO富集分析³⁷使用默认设置和Revigo³⁸总结和可视化结果。

配体受体分析，以识别内皮LPC1和LPC0之间的细胞细胞通信变化

为了对比两种内皮LPC亚型的配体传播与组织中相邻的细胞类型（图 5e），我们对CellphonedB使用了修改（Goeva等，准备中）³⁹。我们根据测试统计量的符号将每次相互作用的输出分离为三个垃圾箱（补充图。 15）和p - 在图中反映的价值：相对于LPC0，在LPC1中显着耗尽（不显着）（p-价值\（\ ge 0.05 \）），并且相对于LPC0显着富含LPC1。统计和再现性对隐藏的数据进行了评估，该数据源自两个公开可用的数据集和一个新颖的数据集，并在这些数据集中使用尽可能多的样本（不使用统计方法来预先确定样本量，并且在分析中没有排除数据）。

根据标准实践进行预处理步骤，并为每个数据集进行独立报告。

涉及在先前发布的公开可用数据集上运行计算方法的实验不需要随机化。研究人员在实验和结果评估过程中并未对分配视而不见。有关研究设计的更多信息，请参阅本文链接的《自然投资组合报告摘要》。

报告摘要

有关研究设计的更多信息可在 自然投资组合报告摘要链接到本文。