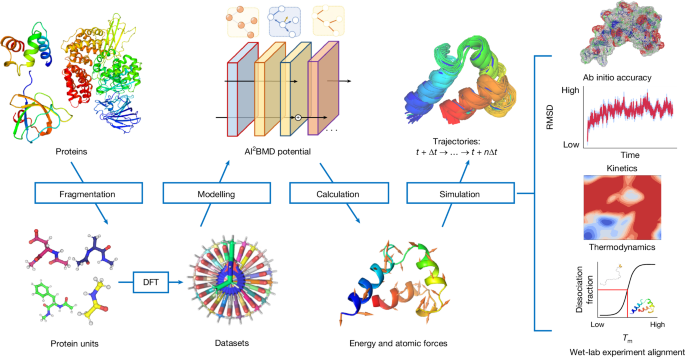
使用 AI2BMD 从头开始​​表征蛋白质分子动力学

随着计算模拟模型的准确性与湿实验室实验的准确性变得难以区分，生命科学研究范式正在发生变化^1,2。在计算模型中，分子动力学 (MD) 模拟就像“计算显微镜”，对于理解生命如何运作特别有意义^3,5,8。MD 模拟通过移动分子系统中的原子来研究分子的动态演化。它们的不同之处在于计算力的方式³。在经典MD中，力是使用规定的原子间势函数来计算的，而在从头算MD（AIMD）中，力是使用从分子电子结构导出的势来计算的⁶。AIMD 提供分子的准确表征；将 AIMD 应用于生物分子模拟的主要挑战是可扩展性。一方面，广泛使用的 AIMD 量子化学方法的计算成本较高；例如，对于系统规模 N，密度泛函理论 (DFT) 的时间复杂度约为\(O({N}^{3})\)，以及包含单次、双次和微扰三重激励的耦合聚类方法 (CCSD(T)) 为\(O({N}^{7})\)。另一方面，观察蛋白质等生物分子的重要构象变化通常需要数十亿个步骤，对于数千个原子来说至少具有立方时间复杂度⁴。到目前为止，针对生物分子的可扩展且准确的 AIMD 还不存在。

为了缓解这一困境，根据 DFT 级别生成的数据进行训练的机器学习力场 (MLFF) 可以以更低的成本提供准确的力计算，并且可以应用于小肽和蛋白质^7,9,10。泛化能力是生物分子模拟的适用性和稳健性的关键挑战¹¹。首先，由于分子的构象空间巨大，对一种分子的有限构象进行训练并使其适应其他种类分子的构象空间探索是很困难的⁵。其次，由于用 DFT 生成数据的时间和成本随着分子大小的增加呈三次方增加，训练数据的缺乏阻碍了 MLFF 在大生物分子中的应用¹¹。此外，不可能为每种蛋白质训练特定的模型，需要具有良好泛化能力的统一解决方案。

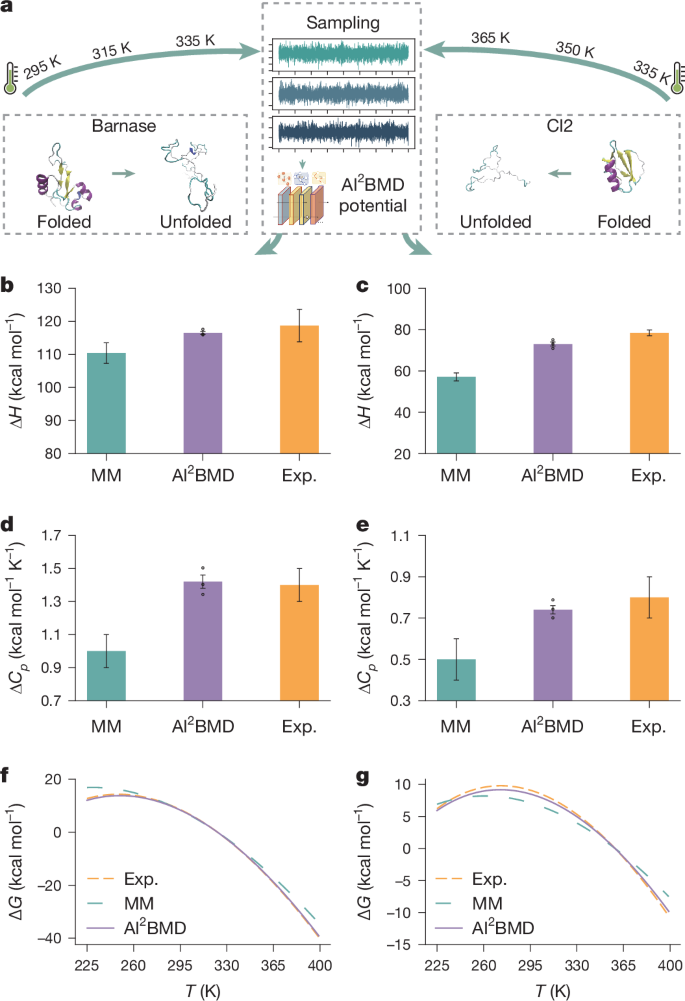
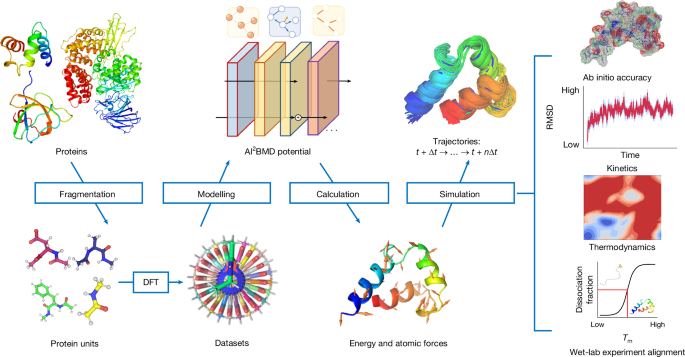
在这项研究中，我们提出人工智能²BMD 是一种通用解决方案，可从头开始准确地有效模拟各种全原子蛋白质，周围环绕着由极化力场建模的显式溶剂（图 1）。1）。一种通用的蛋白质片段化方法将蛋白质分裂成重叠的蛋白质单元。模拟由 AI 执行²弹道导弹防御模拟系统。在每个模拟步骤中，AI²BMD 潜力，基于 ViSNet⁷，从头开始准确计算蛋白质的能量和原子力。通过从动力学和热力学两个角度综合分析，AI²BMD 与湿实验室实验数据（例如快速折叠蛋白质的熔解温度）表现出良好的一致性，并检测到与分子力学 (MM) 不同的现象。

蛋白质通过断裂过程分成蛋白质单元。人工智能²BMD潜力是在ViSNet的基础上设计的，数据集是在DFT级别生成的。它计算整个蛋白质的能量和原子力。人工智能²BMD模拟系统建立在这些组件的基础上，为模拟蛋白质的MD提供了一个通用的解决方案。它实现了能量和力计算的从头算精度。通过从动力学和热力学两个角度综合分析，AI²BMD 与湿实验室实验数据表现出良好的一致性，并检测到与 MM 不同的现象。

为准确模拟蛋白质、AI 提供通用解决方案²BMD 采用通用的蛋白质片段化方法。尽管为特定类型的蛋白质生成样本并在其上训练 MLFF 很简单，但使用 MLFF 模拟其他类型的蛋白质通常会导致模拟崩溃¹²（补充图。1）。此外，在 DFT 级别生成大型蛋白质的训练数据在计算上是令人望而却步的。因此，我们将蛋白质片段化成更小的单元，特别是二肽，计算单元内和单元间的相互作用，然后将它们组装起来以确定作用于原子的蛋白质能量和力（参见 方法了解更多详情）。我们的碎片方法仅包含21种蛋白质单元，并且所有蛋白质单元具有相似且适中的原子数量（范围从12到36），这便于DFT数据生成和MLFF训练。而且，各种蛋白质都可以分解为21种蛋白质单元，表明这是一种可推广的破碎方法。

我们建立了一个全面采样的蛋白质单位数据集。在数据集构建过程中，我们扫描了所有蛋白质单元的主链二面体以涵盖广泛的构象，并使用 6-31g* 基组和 M06-2X 泛函进行 AIMD 模拟¹³，因为该函数可以很好地模拟色散和弱相互作用，并已广泛用于生物分子^14,15。我们获得了 2088 万个样本（参见 方法了解更多详情）。整个数据集分为训练集、验证集和测试集来训练 ViSNet⁷模型作为人工智能²骨密度潜力。该模型对基于物理的分子表示进行编码，并以线性时间复杂度计算四体相互作用。该模型随后根据原子类型和坐标作为输入生成精确的力和能量估计（方法和扩展数据图1）。人工智能的表现²在测试集上将 BMD 潜力与传统 MM 力场进行比较，结果见补充表1。就能量平均绝对误差（MAE）而言，AI²BMD 潜力优于 MM 力场大约两个数量级（AI²BMD：0.045～kcal～mol^Ø1，MM：3.198·kcal·mol^Ø1）。人工智能²BMD 潜力还证明了 MAE 力的卓越性能（0.078-kcal-mol^Ø1Ø…^Ø1）与 MM（8.125—kcal—mol^Ø1Ø…^Ø1）。总体而言，人工智能²BMD 势可以准确预测蛋白质单元的势能和原子力。

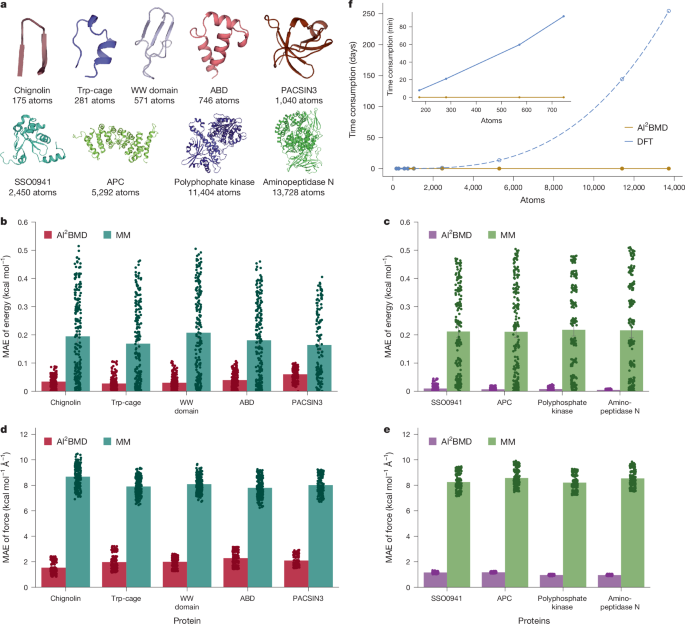
在人工智能的基础上²BMD 潜力，我们开发了一个 MD 模拟系统，采用 AMOEBA 力场描述的可极化溶剂¹⁶（参见方法了解更多详情）。然后我们对原子数从 175 到 13,728 的 9 个蛋白质进行了模拟（图 1）。2a;看到方法了解更多详情）。每个蛋白质均使用源自复制交换 MD 模拟的 5 个折叠、5 个未折叠和 10 个中间结构作为初始构象以及 10 个 AI 进行评估²运行 BMD 模拟步骤，得到每种蛋白质 200 个结构。人工智能2^{通过将 BMD 模拟系统的结果与 DFT 计算的结果进行比较，评估了 BMD 模拟系统达到从头算精度的能力。}MM 的计算作为对照（图 1）。2b-e）。用于评估势能（图1）2b、c），MM 表现出比 AI 更广泛的误差分布和更高的误差上限（即最大误差）²弹道导弹防御。MM势能的平均MAE始终徘徊在0.2·kcal·mol左右^Ø1每个原子，而人工智能²BMD 达到了低得多的值（0.038—kcal—mol^Ø1每个原子，五个蛋白质的平均值）（图 1）2b）。随着蛋白质大小从 chignolin（175 个原子）增加到 PACSIN3（1,040 个原子），能量误差的增加可能归因于对蛋白质单元之间不断升级的多体相互作用的建模不足。对于从具有2,450个原子的SSO0941到具有13,728个原子的氨肽酶-N的蛋白质，只能通过碎片DFT来确定参考值（图1）。2c）。对于这四种蛋白质，AI²BMD 性能（MAE 为 7.18 - 10^Ø3～千卡～摩尔^Ø1每个原子）明显优于MM（0.214-kcal-mol^Ø1每个原子）。从力的角度来看（图1）2d,e），与MM力场相比，AI²BMD 与 DFT 结果更加一致。对于前5个蛋白质直接通过DFT、AI计算²BMD 的平均 MAE 为 1.974—kcal—mol^Ø1Ø…^Ø1与 MM 的 8.094 kcal-mol 相比^Ø1Ø…^Ø1（如图。2d）。对于最后四种大蛋白质，AI²BMD 的平均 MAE 为 1.056 — kcal — mol^Ø1Ø…^Ø1，而 MM 的值为 8.392—kcal—mol^Ø1Ø…^Ø1跨越四个系统（图 1）2e）。我们进一步比较了AI的性能²不同构象的 BMD。如补充图中所示。2—4，分析了每种蛋白质的未折叠构象、中间构象和折叠构象的势能MAE值。不同蛋白质的不同构象势能MAE值存在波动，而原子力MAE值从展开构象到折叠构象略有增加。不同蛋白质和构象的最小 MAE 强调了 AI 从头开始​​的准确性²弹道导弹防御系统。

，九种评估蛋白质的折叠结构。对于这些蛋白质，原子数范围为 175 至 13,728。乙—e, 势能的 MAE (乙,c）和原子力（d,e）。对于每种蛋白质，我们进行了复制交换 MD 和结构聚类来选择代表性结构，包括折叠、未折叠或中间状态。人工智能2^{对代表性结构进行了BMD模拟，共选取200个样本进行评价。}对于 1,040 个原子内的前 5 个蛋白质，如图所示乙,d，在数据集生成中使用相同设置对 ORCA 执行的整个蛋白质进行 DFT 计算，将其设置为参考值，而对于图中所示的最后 4 个蛋白质c,e，由于计算成本过高，参考值被设置为片段DFT计算。在乙,c，每个结构的势能减去初始折叠结构的势能，然后用原子数归一化。误差线在乙—e表示 200 个不同蛋白质样品的势能和原子力的标准偏差（n–= –200)，每个样本显示为实心圆圈。f, 九种蛋白质能量计算耗时对比。DFT 计算在 GPU 上进行。对于最后五个蛋白质，DFT 的时间消耗是通过前四个蛋白质的拟合曲线来估计的，并用虚线和圆圈显示。插图显示了前四种蛋白质的比较。

源数据

此外，为了检验人工智能的效率²BMD，我们比较了AI对所有九种蛋白质的能量计算的时间消耗²具有图形处理单元 (GPU) 支持的 BMD 和 DFT 计算软件。在图中。2f，我们给出了 AI 的计算时间²在具有 A6000 GPU 卡（48 GB GPU 内存）和 32 个中央处理单元核心的台式机上进行 BMD 和 DFT。很明显，人工智能2^{BMD 比 DFT 更快地实现从头算精度。}AI的计算时间²BMD 表现出近乎线性的增长。人工智能²BMD 需要 0.072 秒才能对包含 281 个原子的 Trp 笼执行模拟步骤，而 DFT 则需要 21 分钟。对于具有 746 个原子的白蛋白结合结构域，AI 的时间略微增加至 0.125 秒2^{BMD 与 DFT 的 92 分钟相比。}对于具有 13,728 个原子的较大蛋白质氨肽酶 N，为 2.610 秒，DFT 计算不可行，预计时间超过 254 天，比 AI 慢 6 个数量级以上2^{弹道导弹防御。}我们进一步比较了AI²BMD 的仿真速度与其他人工智能驱动的仿真系统（包括 DPMD）的仿真速度相当^{17 号}和快板¹⁸，以及 Tinker 8 中实现的 AMOEBA 力场和 Amber 中实现的 ff19SB。如扩展数据表所示1， 人工智能2^{尽管 DPMD 使用更简单的模型架构，但除了最小的蛋白质 chignolin 之外，BMD 的模拟速度比 DPMD 更快。}人工智能²在所有情况下，BMD 的仿真速度都大大超过了 Allegro 和 AMOEBA。此外，DPMD 和 Allegro 在 A6000 GPU 卡上处理某些大型蛋白质时都遇到了“内存不足”错误，而 AI²BMD 效果很好。此外，非极化力场表现出最快的模拟，比 AI 快大约一个数量级²弹道导弹防御。综上所述，人工智能²BMD 用途广泛，可推广到各种蛋白质，并为 MD 模拟提供从头算精度和高效计算。

展示AI的能力²BMD用于构象空间探索和蛋白质动力学，我们开展了AI²蛋白质二肽和蛋白质的 BMD 模拟。我们最初构建了天冬酰胺二肽（Ace-N-Nme），其中氨基酸被乙酰基封端，氮-甲基氨基分别位于其氨基和羧基末端，在 5-× 水箱中，并通过使用量子力学 (QM) 进行 500-ps 模拟来对溶质和溶剂之间的氢键进行采样 -MM、AI2^{具有可极化嵌入的 BMD 和具有琥珀色 ff19SB 的 MM。}然后我们扫描水分子中的氧与二肽上的受体之间的距离，并通过纯QM、AI计算整个系统的能量波动²BMD 和 MM。如扩展数据图所示。2a,b，水分子中的氧与主链上氢键受体之间的距离分布，由 QM–MM 和 AI 采样²BMD表现出高度相似性。人工智能²BMD 还表明，在氢键扫描中，能量分布与 QM–MM 比 MM 更加一致（扩展数据图 1）。2c）。此外，人工智能²与 QM–MM 相比，BMD 显示出与水侧链氢键一致的 O–O 距离分布（扩展数据图 1）。2d-f），两个 AI 的峰值²BMD 和 QM–MM 位于相同位置。总之，氢键采样和扫描实验表明人工智能²BMD 可以准确地模拟溶剂效应以及溶质与溶剂之间的相互作用。

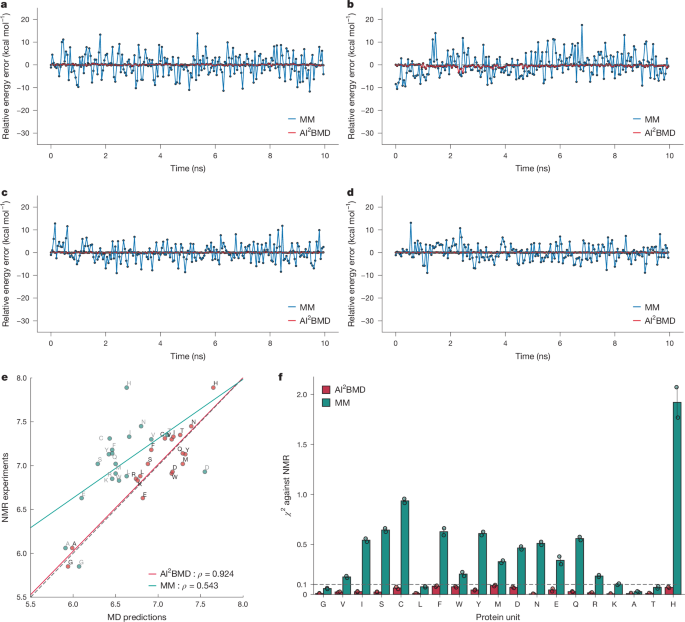
然后我们对不同蛋白质单元的构象空间进行了全面采样。我们首先评估了人工智能生成的模拟过程中势能和原子力计算的准确性²弹道导弹防御系统。人工智能²用10×水箱对每种二肽进行10×ns的BMD模拟，并从模拟轨迹中均匀选取200个带溶剂的快照。通过QM计算整个蛋白质的能量和力，并以溶剂部分的AMOEBA力场作为参考值。MM 计算用于比较。在各种模拟轨迹中，无论涉及哪种蛋白质单元，整个系统的相对能量和力都由人工智能计算得出2^{与参考值相比，BMD 显示出可忽略不计的误差。}相比之下，纯 MM 与参考值有很大偏差（图 1）。3a 至 d和补充图。5和6）。具体来说，对于带负电荷的蛋白质单元 Ace-E-Nme（图 1）。3a）， 人工智能²模拟过程中BMD与参考值相比略有差异（MAE：0.183·kcal·mol^Ø1），而 MM 则表现出明显的差异，MAE 为 4.111 kcal-mol^Ø1。此外，对于Ace-R-Nme，MM计算的能量也出现波动，与参考值存在明显差异（MAE：4.286·kcal·mol^Ø1与人工智能²BMD MAE：0.477—kcal—mol^Ø1;如图。3b）。此外，人工智能²对于侧链带有苯环的 Ace-F-Nme，BMD 始终大幅优于 MM（MM MAE：2.997–kcal–mol^Ø1与人工智能²BMD MAE：0.091—kcal—mol^Ø1） （如图。3c）。具有较小的侧链，例如 Ace-S-Nme（图 1）。3d），AI之间的差异²BMD和参考值进一步减小（MAE：0.056—kcal—mol^Ø1），而 MM 则保持明显（MAE：2.788—kcal—mol）^Ø1）。对于原子力的评估，AI²BMD 还表现出对参考值更高的保真度（MAE：0.002-kcal）^Ø1Ø 摩尔^Ø1Ø…^Ø1）比MM（MAE：0.132—kcal—mol^Ø1Ø…^Ø1）对于 10 ns 模拟中的所有情况（补充图 1）6）。因此，人工智能²在模拟过程中，BMD 保持了多种蛋白质单元的准确性。

—d, 带负电的 Ace-E-Nme 10 ns 模拟过程中整个系统势能的误差 (一个), 带正电荷的 Ace-R-Nme (乙), 芳香族 Ace-F-Nme (c) 和极性 Ace-S-Nme (d）。以整个蛋白质的QM和溶剂部分的MM对整个模拟系统的计算作为参考值，并通过MM进行比较。每个结构的势能减去参考结构的势能，然后通过与参考值比较来计算误差。模拟过程中整个系统的势能波动范围约为300—kcal—mol^Ø1（见补充图7了解更多详情）。e, 核磁共振比较3^J（H氮_,—Hα_{) 联轴器以及由人工智能驱动的模拟衍生的联轴器}2^{BMD 和 MM。}这³J（H_氮,—H_α) 源自 AI 的联轴器²BMD 和 MM 分别显示为红点和绿点。对于每种方法，都会绘制线性回归曲线，并在图例中显示相应的皮尔逊相关性。f,ϲ再现错误³J（H_氮,—H_α) 通过 NMR 测量的每个蛋白质单元的耦合。AI产生的结果²BMD 和 MM 分别以红色和绿色显示。在e,f，王牌-X-Nme二肽缩写为X为了简单起见。脯氨酸二肽由于其独特的键合模式而被忽视。误差线在f表示标准差Ï2^{使用不同初始模拟配置进行的两次重复实验产生的误差（}n�=�2) 对于两个 AI2^{BMD 和 MM。}源数据

我们进一步全面采样了不同蛋白质单元的构象空间。

对于每个蛋白质单元，我们进行了 100 次独立的 AI²BMD 模拟。为了提高模拟效率，首先从全面采样的 MM 轨迹中得出 50 个初始结构。然后，每个初始结构都经历了两次独立的人工智能²BMD 模拟使用显式溶剂运行 1,000ps，从而实现微秒级 AI²蛋白质单位的 BMD 模拟。然后我们分析了人工智能探索的构象空间²BMD 通过复制³J（H_氮,—H_α）通过核磁共振（NMR）实验测量的耦合^13,19。这³J（H_氮,—H_α）耦合可以准确地反映Ï肽的角度分布¹³因此从实验的角度采用了通过模拟蛋白质单元来测量构象空间探索。排除脯氨酸和组氨酸二肽，我们计算了³J（H_氮,—H_α) 其他18种蛋白质单元基于主链的耦合值ÏAI 衍生的角度²BMD 模拟轨迹，然后对两次平行重复的值进行平均以获得最终估计。作为比较，MM制作的那些报告在ff19SB力场中²⁰。数字3e说明那些由人工智能驱动的模拟²BMD 表现出显着更高的皮尔逊相关性（ÏNMR 实验测量值与 MM 计算值的比较（==0.924）Ï≤=≤0.543）。此外，人工智能²如图 1 所示，所有蛋白质单位的 BMD 均明显优于 MM。3f。这些结果进一步凸显了人工智能的有效性²从湿实验室实验角度进行构象探索和采样的 BMD。

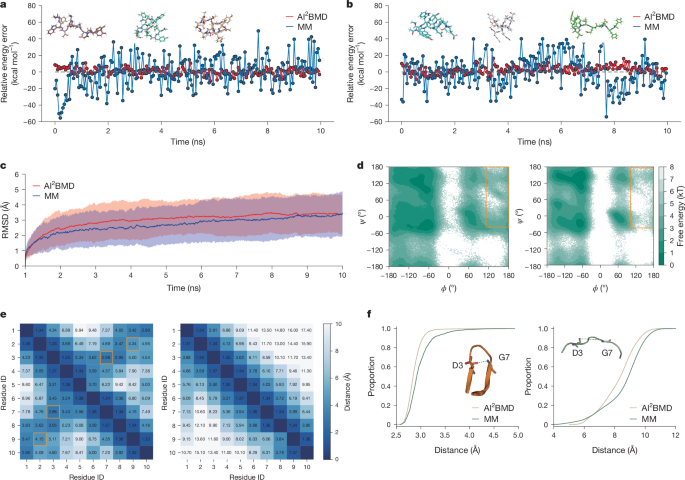
然后我们进行了AI²十肽 chignolin 的 BMD 模拟²¹在显式溶剂中研究人工智能采样的动力学差异²弹道导弹防御。从折叠或展开结构开始总共进行了 60 次模拟，每次模拟时间长达 10 纳秒。人工智能²BMD 在模拟过程中捕获了 chignolin 的折叠和展开过程。在图中。4a和补充图。7a，从展开的结构开始，蛋白质形成折叠的发夹结构，并带有堆积的β链。在此过程中，AI的相对能量误差²BMD为3.44kcalmol^Ø1，而 MM 的热量为 15.20—kcal—mol^Ø1。相比之下，如图。4b和补充图。7b描绘了从折叠的发夹结构到延伸的展开结构的展开过程。在此过程中，AI计算出的值²BMD与参考值相差4.40-kcal-mol^Ø1，而 MM 的偏差为 15.11-kcal-mol^Ø1。在这两个仿真过程中，如补充图所示。8，与力误差0.614—kcal—mol相比^Ø1Ø…^Ø1用于折叠过程和0.620-kcal-mol^Ø1Ø…^Ø1MM、AI制作的展开过程²BMD 还表现出与参考值更接近的力计算（力误差为 0.063 — kcal — mol^Ø1Ø…^Ø1折叠过程中力误差为0.073—kcal—mol^Ø1Ø…^Ø1用于展开过程）。此外，从图1所示的模拟中投影构象。4a在自由能景观上可以观察从展开亚稳态到具有最低能量值的折叠亚稳态的折叠过程（扩展数据图 1）。3）。这些结果表明人工智能²BMD 可以自行折叠蛋白质并检测有意义的构象变化以研究蛋白质动力学。

,乙, 从展开结构开始对 chignolin 进行 10 ns 模拟期间整个系统的相对势能误差（一个）和折叠结构（乙）。整个蛋白质的QM计算和剩余溶剂部分的AMOEBA力场计算作为参考值。相对能量定义为每个结构的势能减去参考结构的势能。模拟期间的初始、中间和最终结构显示在顶部。模拟过程中整个系统的势能波动范围约为500—kcal—mol^Ø1（见补充图9了解更多详情）。c，RMSD 在 10 纳秒模拟的 60 个轨迹的集合中（前 1 纳秒被省略）。平均 RMSD 显示为一条线，所有 60 个模拟轨迹的范围以阴影显示。d, AI 采样的 Ramachandran 构象图2^{BMD（左）和 MM（右）在 10 ns 模拟的 60 条轨迹的集合中。}不同的区域用黄色矩形突出显示以便可视化。e，折叠（左）和展开（右）结构的剩余最小距离图。人工智能²BMD和MM分别显示在下三角矩阵和上三角矩阵中。α-β相互作用和氢键用黄色方块突出显示以供分析。f，折叠（左）和展开（右）结构的 D3 主链 O 和 G7 主链 N 之间距离的累积图。源数据

进一步探索人工智能驱动的奇诺林动力学差异

2^{BMD和MD，我们也用相同的初始结构和模拟配置用MM进行了模拟，发现AI2}BMD 模拟展示了几个不同的特征。^{首先，AI进行模拟2}BMD 表现出与 MM 相似的结构波动。^{如图所示。}4c，与 AI 中的初始结构相比的均方根偏差 (RMSD)2^{在最初的几纳秒内，BMD 模拟的增长速度略快于经典 MD 模拟的速度，并且随着模拟的收敛，差距逐渐消失。}10 秒后，AI²BMD 的平均 RMSD 为 3.378%，而 MM 模拟达到 3.454%。我们还分析了模拟过程中相邻 Cα 原子的距离。如补充图所示。9，AI模拟²BMD 显示出与 MM 相似的分布。AI 中相邻 Cα 原子之间的平均距离为 3.816 和 3.863²BMD 和 MM 分别接近经验值 3.8，这意味着模拟运行稳定，没有出现模拟崩溃。其次，关于 Ramachandran 图（图 1）中描绘的特定主链构象。4天）， 人工智能²BMD 的分布比 MM 稍宽，特别是在以下区域：Ï范围从 120° 到 180°Ï范围从 60° 到 180°。我们进一步研究了人工智能之间的差异²BMD和MM通过检查每个残基的Ramachandran图，发现这种差异主要来自于Ï—ÏG7的角度分布（扩展数据图1）4a,b）。如扩展数据图所示4c、d，然后我们根据Ï和ÏG7 的角度并呈现每个簇的代表性结构。人工智能²BMD表现出更加多样化Ï和Ï与 G7 的 MM 角度相比。考虑到由于缺乏侧链，甘氨酸可以探索 Ramachandran 图上的大部分区域^{22 号}，模拟过程中的观察结果表明人工智能²BMD 可以探索更多可能的构象空间，而无需 MM 中应用的键长谐波约束。

此外，使用问分数，根据模拟期间的接触来评估蛋白质折叠²³，我们将AI分开²BMD 和 MM 快照为折叠和展开结构。如残差最小距离图所示（图2）。4e），AI的结果²BMD 和 MM 在折叠和展开结构上相似。他们都描述了 chignolin 的 N 端和 C 端芳香残基 (Y2-W9) 与 D3 和 G7 之间的氢键之间的稳定相互作用。对于 D3 和 G7 之间最强的氢键（参考文献。）^21,24），AI采样的折叠构象²BMD 将其描述为更稳定（AI 中的最小距离为 2.86）2^{BMD 与 MM 中的 2.98% 相比）。}D3主链O与G7主链N之间距离的累积图（图1）4f）也说明了人工智能²BMD 比 MM 更稳定氢键。对于展开结构，人工智能的趋势²BMD 和 MM 的相似之处在于，两者都描述了比折叠结构中的距离长得多的距离。这些结果表明，通过从头开始精确地执行模拟，人工智能²BMD 可以检测有意义的构象变化和详细的原子间相互作用，以研究蛋白质动力学。观察到的差异可能归因于人工智能²BMD 不会对键和角度施加谐波约束，从而提供更大的灵活性和更接近现实条件的条件。

检查人工智能的有用性²BMD在蛋白质性质评估中的应用，我们首先研究了AI模拟的各种快速折叠蛋白质的热力学性质²弹道导弹防御。来自参考文献全面采样的蛋白质轨迹。⁴，我们为每种蛋白质均匀获取 100,000 个快照，并使用问– 得分以将它们分类为折叠和展开状态。七种蛋白（即 BBA、WW 结构域、NTL9、同源结构域、蛋白 G、α3D 和 α-阻遏蛋白）的代表性折叠和未折叠结构显示在扩展数据图 1 中。5a。这些蛋白质由 504 至 1,258 个原子组成，具有多种二级结构。聚类分析表明，对于每种蛋白质，折叠簇中心的结构与相应的折叠晶体结构紧密排列（补充图 1）。10）。我们首先通过AI计算出势能值²BMD 并使用时滞独立分量显示势能面。如扩展数据图所示5b对于 NTL9 的情况，对于 MM 和 AI 产生的结果²BMD、折叠和展开结构明显分开，具有不同的势能，尽管它们之间的势能差异在人工智能中较小²BMD 结果。通过重新加权势能值，我们估计了蛋白质折叠过程中的自由能差异（ÎG）和熔化温度（时间_米）源自模拟轨迹（扩展数据图 1）5c、d和补充表2）。因此，蛋白质模拟是在相应的熔化温度附近进行的⁴, ÎG预计会更接近 0，计算得出时间_米预计更接近模拟温度。MM和AI都可以²BMD 实现了较小的自由能差异，并且计算的熔化温度与模拟温度相当，尽管 AI²在这些情况下，BMD 的表现略优于 MM。

值得注意的是，WW 结构域是评估中唯一由 β-sheet 主导的蛋白质²⁵。与实验确定的 WW 域熔化温度 371±±2–K 相比²⁵，估计时间_米由人工智能提供²BMD（359.06±0.07±K）比MM（353.69±±0.38±K）更接近。NTL9 具有带有 α 螺旋和 β 片层的折叠结构²⁶。模拟温度为355℃，与实验温度基本一致时间_米NTL9 的 354.75±±1.7–K（参考。²⁷）， 人工智能²BMD 更好地估计了 αG比MM（≤0.34≤kcal≤mol^Ø1相对于 1.54 kcal molØ1^）。此外，人工智能²BMD估计时间_米为351.84±±0.11±K，比MM给出的349.47±±0.35±K更准确。

此外，对于所有 α 蛋白，同源域具有具有三个 α 螺旋和环的折叠结构²⁸。虽然人工智能²BMD 的 ÎG估计（≤0.18≤kcal≤mol^Ø1) 小于 MM s (±0.73–kcal–mol^Ø1）， 他们的时间_米预测几乎相同（AI²BMD：359.61±±0.14±K；MM：359.60±±0.13±K）并且与实验相当时间_米>372–K（参考。–²⁹）。α3D 是一种主要由 α 螺旋组成的人造蛋白质³⁰。人工智能²BMD 的 ÎG估计为～0.098～kcal～mol^Ø1，而 MM-s 为 1.33-kcal-mol^Ø1。AI 生成的熔化温度分别为 369.67±±0.06–K 和 366.94±±0.26–K2^{BMD 和 MM 分别与实验值相当 (>363–K)}31^{对于 α3D。}α-阻遏蛋白是评估中最大的蛋白质，以α-螺旋为主³²。人工智能²BMD 和 MM 的 γ 均偏离 0G估计（人工智能²BMD：0.79·kcal·mol^Ø1;MM：1.09～kcal～mol^Ø1），但是人工智能²BMD 更接近。他们的时间米_{估计几乎相同（AI}2^{BMD：349.55±±0.21±K；}MM：349.48±±0.21±K），接近实验值（347±K）³²。

对于 α- 和 β- 蛋白质，BBA 具有由 α-螺旋和 β-发夹组成的折叠结构³³。由于缺乏已知的熔化温度，模拟在 325°K 下进行。人工智能2^{BMD 的 Î}G计算（0.057—kcal—molØ1^{） 和}时间米_{估计 (323.94±±0.22–K) 与 MM 的结果 (1.22–kcal–mol}Ø1^{和 322.34±±0.31±K）。}蛋白 G 由 α 螺旋和四重 β 片层组成34。^人工智能2^{BMD 的 Î}G预测（0.14—kcal—molØ1^{) 比 MM·s (0.74·kcal·molØ1}）。^{在没有实验的情况下}时间米， 人工智能₂BMD 估计^时间米(349.49±±0.12–K) 与 MM– (346.49–±–0.66–K) 相比，模拟温度提高了 3-K，模拟温度为 350°C_{K 代表蛋白质 G。}我们进一步估计了蛋白质折叠过程中焓和热容的变化。

选择两种状态的蛋白质 110 个残基 barnase 和 84 个残基 CI2 进行评估。从折叠结构和展开结构开始进行了二十次模拟。对于每种蛋白质，在 NPT 系综下在三个不同温度下进行模拟。通过人工智能计算模拟过程中采样的构象的势能值2^{弹道导弹防御。}如图所示。5和补充表3， 人工智能²BMD 在所有评估指标中的计算结果均优于 MM。对于barnase，AI计算出的焓和热容的变化²BMD为116.5±0.43kcal·mol^Ø1和 1.4±±0.04—kcal—mol^Ø1—K^Ø1，按MM计算为110.4±±3.1—kcal—mol^Ø1和 1.0—±0.1—kcal—mol^Ø1—K^Ø1（参考文献。）³⁵）， 分别。与实验测定值118.7±±4.9—kcal—mol相比^Ø1和 1.4—±0.1—kcal—mol^Ø1—K^Ø1（参考文献。^35,36），AI取得的成果²BMD 比 MM 更接近（图 2）。5a、c）。CI2 上也观察到类似的结果，如图 2 所示。5b、d。AI计算出的焓和热容的变化²BMD为73.0±0.97kcal·mol^Ø1和0.7-±0.02-kcal-mol^Ø1—K^Ø1，接近实验测量值78.4±±1.4—kcal—mol^Ø1和0.8±0.1kcalâmol¹k¹（参考^35,37）。相比之下，MM的焓变仅为57.1±1.9kcalâmol -mol¹并且热容量的变化为0.5±0.1kcalâmol¹k¹（参考³⁵）。对于温度的自由能波动，AI²与MM的结果相比，BMD的结果与实验结果更一致（图。5f，g）。这些观察结果进一步巩固了AI的启动能量计算²BMD可以更好地描述蛋白质折叠中的特性。

值是通过MM计算的²BMD和实验（经验）。一个，AI的总体计算方案2^BMD。乙e，焓的变化（H) (乙,c）和热容量（Cp) (_d,e）在蛋白质展开的过程中乙,d）和CI2（c,e）。在乙e，误差线表示的标准误差H和Cp来自具有不同初始仿真配置的三个重复实验的值（n= 3）对于AI₂BMD。MM和实验值的平均值和标准误差来自参考文献。35^。f^,克，针对barnase温度的自由能波动（f）和CI2（克）。源数据此外，我们还展示了AI2通过对酸解离常数负基碱基10对数的案例研究，BMD的实用性在炼金术自由能计算中（P）K

一个

）使用热力学整合估计硫氧还蛋白ASP26³⁸。最初，AI₂将BMD应用于用Asph26和Asp26和二肽ASPH ASP的硫氧还蛋白的模拟轨迹跨模拟轨迹的势值。^{随后，使用热力学整合来计算自由能的差异（}G^{）对于质子化状态从硫氧还蛋白中的Asph26变为ASP26，如扩展数据图所示。}6。估计的pK一个AI的价值7.612BMD与7.5的实验基准密切相对应，并超过了已建立方法的准确性，包括力场，基于经验和基于QM MM的方法。_{鉴于对各种蛋白质的蛋白质特性评估，AI}2^{BMD对构象合奏表现出准确的计算，从而导致对蛋白质折叠热力学的合理估计，并在生化研究中提高了效用。}讨论^{从头开始，模拟生物分子动力学是一个长期存在的挑战，因为很难同时实现准确性，效率和概括能力}5,

。^{我们已经为广泛的蛋白质制定了一个可推广，高效且近距离的初始模拟程序，AI2BMD，对MM的能量和力计算和蛋白质性质估计提供了可观的改进。}AI的普遍性²BMD跨不同蛋白质系统及其鲁棒性展示了其在蛋白质研究中更广泛应用的潜力。^{与QM -MM相比，该MM定义了由QM计算的重点区域和MM计算的其余部分AI2}BMD在没有任何先验知识的情况下将从头算机从小预设QM区域扩展到整个全原子蛋白。

此外，AI²BMD消除了蛋白质边界上QM和MM力学的潜在不相容性，并通过多个阶加速了QM区域计算。^{此外，对于QM MM无法处理的某些复杂的生物分子动力学，例如需要QM处理并在模拟过程中动态进化的聚焦区域或大型QM区域，例如在某些变构法规或本质上无序的蛋白质模拟的过程中，AI2}BMD 可以为未来的研究提供新视角的机会。^{AI的概括能力2}BMD源于大多数蛋白质由常见氨基酸组成的基本原理。

这种理解允许AI²BMD可作为一种多功能且可适应的算法，可应用于多种蛋白质。^{通过将这些知识纳入AI2}BMD，它可以用于蛋白质的各种构象并适应不同大小和组成的蛋白质，使研究人员能够以更高的信心和精度探索和研究蛋白质的复杂世界。^{此外，在蛋白质动力学领域，没有键长度和角度的谐波约束，AI2}BMD合理地将柔韧性纳入蛋白质运动中，这是基于接近全原子蛋白质准确性的计算，将为研究蛋白质动力学创造更多机会。

另外，尽管AI²BMD的计算速度比DFT方法要快得多，它仍然落在经典的MD模拟方面。

为了弥补这一差距，未来可以使用多种策略。^{例如，实施其他工程优化可能会导致AI效率的重大提高2}BMD。^{此外，应用AI2}BMD对于更广泛的系统，包括脂质，核苷酸，纳米材料和溶质溶剂接口，将扩大AI的范围²BMD适用于更复杂的生物分子系统，以将新见解解锁到复杂的生物分子系统世界中⁴⁰,^{41，为在多种情况下（例如药物发现，蛋白质设计和酶工程）中更准确有效的模拟铺平道路。方法}蛋白质断裂方法

二肽是一种氨基酸，分别在其n和câ末端用ACE和NME基团盖住。

由于氨基酸是蛋白质的基本单元，因此我们根据二肽设计了可推广的蛋白质破碎方法，并训练有素的AI2^{相应地，BMD潜力确保了所有蛋白质的概括能力。}肽破碎的概念已经存在了多年，并且先前的研究证明了其对蛋白质的准确性和效率

10,^{42。如扩展数据图所示。}7a，每个二肽包括：主链的所有原子和氨基酸的侧链；Cî±，h连接到先前氨基酸主链的cî±，c，o；N，H，h连接到下一个氨基酸主链的n，cî±和h。我们用滑动窗口切割了多肽链，因此Ace-NME片段充当两个连续的二肽之间的重叠区域（扩展数据图。7b）。根据c的键长以及整个肽链中与Cî±连接的键的方向，将末端Cî±的额外氢元素添加到二肽和ACE-NME片段中。如果第一个或最后一个氨基酸是甘氨酸，则根据C的键长仅添加一个与Cî±连接的氢。如果后一种氨基酸是脯氨酸，我们还根据n连接到Cî'的N键长度，添加了连接到N的氢。然后，有限的内存BroydenâFletcher-GoldfarbâshannoQuasi-Newton算法⁴³在其他部件受到约束时，应用于优化添加氢的位置。

我们首先通过总结二肽的能量来计算所有蛋白质单元的总能量和力，从1））。

其中n是氨基酸或二肽的数量。在公式之后计算同一二肽和ACE-NME中原子的力（

2）。$$ {f} _ {i}^{{\ rm {\ rm {fact}} \ _ {\ rm {units}}} = \ m athop {\ sum} \ limits_ {j = 1}

其中我表示原子进行力计算，米代表所有二肽原子我属于，n代表所有Ace-nme碎片原子我属于和j代表与原子共存的任何其他原子我在同一二肽或ACE-NME中。我们进一步补充了非重叠蛋白质单元之间的额外相互作用。

补充图。18显示了四肽不同蛋白质单位之间的额外相互作用。没有计算相互作用的两部分。扩展数据图8a说明CH组之间的额外相互作用¹,C¹, 氧¹和NH¹（以紫色概述）和四肽的最后一部分（也以紫色概述）。此外，扩展数据图。8b在四肽的开始部分之间展示包括CH3的额外相互作用⁰,C⁰, 氧⁰和NH¹（以棕色概述）和另一部分从第二侧链开始到câcâcâterinus（也以棕色概述）。

考虑到这些非重叠区域中的相互作用以静电力和范德华相互作用为主，我们使用库仑方程和伦纳德-琼斯势来描述它们。然后，我们使用了从琥珀FF19SB力场得出的相应参数²⁰以及原子之间的距离以计算额外相互作用的势能和原子力（方程式）（3） 和 （4））。与另一个广泛使用的力场相比，FF19SB的选择在评估相对能量方面的出色表现得到了了解（参考文献。⁴⁴），如补充图所示。11。

其中具有上标单位的能量和力代表从等式获得的值（1）到公式（2）， 和一个表示相应单元中的原子集。为了避免重复计算，总和遍历索引在当前原子之后的所有原子。

通过蛋白质裂解的方法，所有蛋白质都可以转换为21种蛋白质单元（即20种二肽和另一种Ace-Nme），大大减少了特定类型蛋白质单元的数量，有利于数据集构建和模型训练，有助于探索整个构象空间，避免势能面出现空洞，从而提高MD模拟的泛化性、效率和鲁棒性。

蛋白质单位数据集

AI的培训数据集²通过以下协议生成BMD电位。首先，Ambertools20的TLEAP模块中的序列命令（参考 ⁴⁵）用于生成最初20种二肽和ACE-NME的拓扑和协调文件。然后， -（也就是 -（也就是说，nâcî± - n的二面二维在180°至175°的范围内进行了二维扫描，间隔为5°。对于脯氨酸二肽， -由于其环形构象，二面体从180°到120°进行了完善。二面体的旋转是由cpptraj中的旋转型司令部完成的⁴⁶。对于每个非脯氨酸二肽，生成了 5,184 个锚点。对于ACE-NME，在ACE和NME的nme的C轴上施加了在180°至175°的范围内扫描范围为5°，导致72个锚。

每个锚首先遇到几何优化（GO）过程以获得合理的结构。GO 过程中使用溶剂化模型密度 (SMD) 溶剂模型。这 -和 -二核也受到与锚生成相同的约束。对于每个锚点，GO 过程的最后一个结构被用作 AIMD 模拟的输入结构。通过考虑 QM 中的溶剂效应，使用 SMD 对构象进行采样。对于二肽，对每个锚点应用 225-fs 模拟，并提取最后的 200-fs 结构。为ACE-NME进行了2,025 fs的模拟，并为每个轨迹提取了最后2,000 fs。由于在我们的AI驱动的MD模拟中使用了明确的溶剂2^{在AIMD模拟之后，BMD电位重新计算了所有提取的没有SMD的提取构象的单点能量和力，这些构型用于MLFF训练。}在GO期间，使用了6-31G*基集的M06-2X密度的DFT，AIMD模拟和单点能量计算。

47^。此基集和功能通常适用于生物分子采样^14,15,48,49。我们在模拟过程中设置了严格的收敛条件，并且收敛是下一步计算的强制要求。系统通过速度重新升级恒温器在290 k中遇到了典型的采样（参考文献。⁵⁰）。此类模拟由Orca 5.0.1进行（参考文献。⁵¹）。根据Phâ7时所有氨基酸的总和的电荷设置每个系统的电荷。GO，AIMD模拟和单点能量计算需要大约12,928,993个中央处理单元（CPU）核心小时（1,476 CPU核心年）进行计算。结果，每种二肽在DFT水平上采样并计算了1,036,800个构象，并且Ace-Nme采样并计算了144,000个构象。在补充表中显示了每种蛋白质单位的能量分布和力规范4和5和补充无花果。12和13。整个蛋白质单元数据集由2000万个构象组成，可全面捕获蛋白质单元的构象空间，并为机器学习潜在的培训和AI提供了坚实的保证2^BMD模拟。Visnet作为AI

2^BMD电位Visnet是一种多功能的几何深度学习模型

7^{,52可以通过将原子坐标和原子数作为输入来预测势能和原子力以及各种量子化学性质。}如补充图所示。2a，Visnet模型由嵌入块和多个堆叠的Visnet块组成，然后是输出块。原子序数和坐标被输入到嵌入块中，然后输入 ViSNet 块来提取和编码几何表示。然后使用几何表示来预测通过输出模块的分子能量和力。补充图。2b演示Visnet块，该块由消息块和更新块组成。这些块作为矢量标量交互式消息传递机制（称为 ViS-MP）的一部分一起工作。通过 ViS-MP 传递的丰富几何信息由运行时几何计算模块以线性复杂度提取。补充图中的操作。2b可以概括如下：

其中\（{h} _ {i}^{l} \）表示节点的标量特征\（我\）在我第层，\（{{\ bf {v}}}} _ {i}^{l} \）表示矢量化节点特征，\（{f} _ {{ij}} \）\）表示节点之间的标量边缘特征\（我\）和节点\（J \）。\（{\ phi} _ {m}^{s} \）,\（{\ phi} _ {m}^{v} \）是非线性消息函数，用于转换来自邻居的消息，\（{\ phi} _ {{un}}}^{s} \）,\（{\ phi} _ {{ue}}}^{s} \）,\（{\ phi} _ {{un}}}^{v} \）是非线性更新函数，根据消息和几何特征更新相应的特征。有关运行时几何计算和VIS-MP的更多详细信息可以在参考文献中找到。⁷。

对于每种蛋白质单元，ViSNet都被训练为节能潜力模型；也就是说，预测的原子力是从势能相对于原子坐标的负梯度得出的。我们将每个蛋白质单元数据集按 8:1:1 的比例随机分为训练集、验证集和测试集。超参数在丙氨酸二肽的验证集上进行调整，并直接应用于其他蛋白质单元。具体来说，所有针对蛋白质单元训练的 ViSNet 模型都相对较轻，只有 6 个隐藏层和 128 个用于节点和边缘表示的嵌入维度。为了更好地捕获几何信息，我们通过调整高阶球形谐波扩展了分子的原始三维坐标⁵³。对于所有蛋白质单位，边缘连接的切口设置为5â，每个原子的最大邻居数量为32。我们利用了能量和强度为0.05和0.95的均值和力训练的组合平方误差损失和强度训练。， 分别。我们采用的学习率为2⁴有1,000个热身步骤⁵⁴使用ADAMW优化器⁵⁵。如果验证损失停止减少，学习率就会衰减。耐心设置为 15 epoch，衰减因子设置为 0.8。我们还采取了一种早期策略来防止过度合适⁵⁶。最大 epoch 数设置为 6,000，提前停止耐心为 150 epoch。所有模型均在 GPU 集群上进行训练，每个集群节点有 16 个 NVIDIA 32G-V100 GPU，根据蛋白质单元的大小，每个 GPU 的批量大小为 64 或 128。为了使模型更好地收敛，对于训练集，我们从总能量中减去了原子参考能的总和，然后用Z - 分数归一化。有关Visnet超参数的更多详细信息可以在补充表中找到6。

人工智能²BMD仿真程序

与AI进行模拟²BMD电位，我们基于原子模拟环境设计了一个AI-drion MD模拟程序⁵⁷。扩展数据图9说明了程序的概述框图。程序启动时，初始蛋白质结构被送入预处理模块，其中添加溶剂和离子，并且结构被松弛。然后整个仿真系统被发送到MD循环，即主要逻辑组件。对于 MD 循环中的每次迭代，蛋白质首先被蛋白质碎片模块分解为碎片，然后由工作调度程序进行分区。分区方案由可调设备策略决定，用户可以根据模拟系统的大小选择指示工作调度程序通过超额订阅来最大限度地提高所有 GPU 的利用率，并减少系统上的内存压力。通过平衡 GPU 卡上不同片段上的计算来控制特定设备。然后，分区的片段和溶剂原子被异步发送到在单独进程中运行的不同计算服务器。这种异步客户端服务器范式有助于减轻Python运行时的实质性限制：只有一个线程可以在同一过程中一次执行Python代码。当工作负载从主组件分配到计算服务器后，它将被并行处理，并且主Python进程可以立即恢复处理其他任务，例如持久化轨迹数据，而不会被服务器阻塞。

考虑到云计算是支持科学计算工作负载的一种流行且经济高效的方式，我们将模拟过程设计为面向云的。软件配置完全由 Docker 镜像定义，并且在不同机器上保持不变，这使我们不仅可以轻松地将软件系统部署到云端，还可以针对一组固定的支持库对程序进行微调。由于基于云的机器可能会被抢占，并且机器本地存储在长时间的模拟过程中是不稳定的，因此我们实现了一个作业调度组件，该组件定期将计算结果保存到基于云的存储并恢复模拟。

模拟中的系统配置

我们使用Amber20软件包与Amoeba 13力场准备了生物分子系统¹⁶。首先将蛋白质溶解在Cutic Tip3p中⁵⁸水箱，然后在能量最小化周期中放松。然后，naCl原子作为柜台和另一个0.15solâl¹添加了缓冲液。我们使用经典的基于琥珀库仑势的方法来添加离子。最初，产生了1字的网格，并计算了所有网格点库仑电势。然后，将离子放置在库仑势对比类型最高的网格上。如果离子与溶剂分子发生空间冲突，则离子会移动到该溶剂分子的中心，并且后者被去除。

仿真系统采用混合计算策略；也就是说，蛋白质是由AI计算的²BMD潜力均具有从头算的准确性，而Amoeba 13力场则用于处理溶剂。系统的总能量（\（{e}^{{\ rm {total}}}} \）) 计算为 ViSNet 计算的深度学习 (DL) 能量的总和 (\（{e} _ {{\ rm {dl}}}}}^{prof} \））对于蛋白质，以及整个系统的 MM 计算的能量（\（{）。然后，为了避免重复计算蛋白质的能量贡献，蛋白质原子相互作用的能量（\（{) 从总能量中减去，如下式所示。这样的计算基于原子模拟环境包装中植入的经典综合分子轨道+mm模型^59,60。

同样，力\（{f} _ {i}^{{\ rm {total}}}} \）\）对于原子我最初是将原子之间相互作用的力设置为我以及蛋白质中的所有其他原子（\（{f} _ {i}^{{\ rm {prof}}}} \）\）），在公式中描绘4）。为了考虑溶剂效应，计算了原子之间的附加力\（我\）以及系统中的其他原子通过Amoeba力场（等式中的第二个项目（11），然后减去溶质项目（等式中的第三个项目（11））。

其中乙代表整个系统中的所有原子，\（c \）代表溶质中的原子。此外，要计算\（{e} _ {{\ rm {dl}}}}}^{{\ rm {prot}}}} \）和\（{f} _ {{\ rm {dl}}}}}^{{\ rm {prof}}}} \），我们首先将蛋白质分为蛋白质单元，通过Visnet模型计算了势能和原子力，然后通过方程组合所有蛋白质单位（3）。有关蛋白质碎片和 ViSNet 电位计算的更多详细信息，请参阅上述部分。在NVE集合下进行的模拟证明了保守的总能量和平衡力，从而进一步证实了随后的采样程序的有效性（补充图2。14和15）。此外，我们还对同一精氨酸二肽在NVT系综下进行了模拟，并通过以下公式计算了热容量：

其中\（\ langle {e}^{2} \ rangle \）表示系统能量平方值的系综平均值，\（{\ langle e \ rangle}^{2} \）表示系统能量的系综平均值的平方值。MM和AI的热容量值²BMD为0.052kcalâmol¹k¹和0.053kcalâmol¹k¹，与以前的实验研究相似，并且相似。这项研究的随后模拟是在Berendsen NVT集合中进行的，其初始速度随机从MaxwellâBoltzmann分布中随机得出。这项研究的时间步骤设置为1 fs。在模拟过程中，轨迹将被写入高精度 XYZ 文件。

模拟细节

在评估蛋白质能量和力量计算时，蛋白质结构（蛋白质数据库（PDB）IDS：chignolin，5AWL;trp笼，2Jof;WW域，2f21;白蛋白结合域，1prb;Pacsin3，6f55;SSO0941，5VFK;APC，5iza;多磷酸激酶，1xdo;氨基肽酶n，4xn9）在概括的隐式溶剂模型中溶剂化。WW结构域的变化遵循上一项研究的GTT突变⁴，除去了白蛋白结合域中的前五个柔性残留物。Amber 程序 makeCHIR_RST 用于在复制交换分子动力学 (REMD) 模拟期间创建手性约束文件，以在高温下保持手性特性。最小化1,000步后，在300 k至1,000 K的温度下进行了200 ps的平衡运行，步幅为100K。最终的平衡结构用于相应温度下的remd模拟。在模拟过程中，每个复制品在每次生产运行中都会与相邻温度和5,000次交换之前进行2 ps的运行。根据Cî±RMSD针对晶体结构，将恢复轨迹分为三个状态。具体而言，对于Chignolin，折叠结构的RMSD为02.5ââ，中间结构的RMSD为2.5（7.5（7.5），而展开的结构的RMSD超过7.5（ -对于其他蛋白质，这三个状态的范围为0ââ€，515â -15ââ和>15â。然后，将折叠和展开状态进一步分为5个簇，中间结构通过cpptraj群集程序分为10个集群。我们挑选了每个聚类中心的结构，总共积累了20个初始结构。最后，将每个初始结构溶解在一个5-tip3p的水箱中，并遇到10步的1-FS AI2^BMD模拟。模拟是在 NVT 系综下进行的。模拟温度（300 k）由Berendsen恒温器控制，并且 -是10 fs。在M06-2X 6-31G*水平上计算相应结构的参考能和力。MM能量和力通过ff19SB力场计算。

对于在ACE-N-NME上进行采样，我们使用tleap中的'序列命令构建了系统，然后应用了一个10-NS remd模拟，与用于蛋白质采样的命令相同。由此，我们使用CPPTRAJ群集程序提取了50个代表性结构。然后，我们使用AI为每个初始结构进行了10 ps模拟²BMD具有可叠式极化嵌入的BMD，导致累积抽样时间为500 ps。我们还使用QMâmM进行了10-PS模拟，并在这些构型上使用Amber FF19SB进行了敏捷的嵌入和MM。每个模拟都包含一个5â的水箱。然后，我们在模拟过程中检查了每个快照，以定位与主链或侧链形成氢键的任何水分子（标准：频率> 90％，供体原子距离<3.5â€角度> 150°）。随后，我们描绘了供体原子距离的分布。形成一个氢键后，我们分离了水和ACE-N-NME分子，并将水从2.5â-4.0â€逐步拉出，形成了150个结构。最后，我们对水分子系统进行了单点能量评估，并在M06-2X的6-31G*水平上通过QM进行了二肽，AI2^{BMD含有变形虫溶剂和MM，带有FF19SB。}对于人工智能

2^{BMD模拟在二肽上，我们首先通过tleap中的序列命令生成了二肽的构象。}然后，将二肽溶解在一个5-− tip3p水箱中，我们在FF19SB力场下运行了两个重复的500-NS经典MD模拟，以进行足够的采样。k然后应用均值聚类，并拾取了50个代表性结构。从代表性结构开始，我们进行了10-NS AI²负电荷蛋白单元ACE-E-NME的BMD模拟，带正电荷的ACE-R-NME，ACE-F-NME，侧链中带有苯环和ACE-S-NME，ACE-S-NME，较小的侧链由A溶解NVT合奏下的10-水箱。此外，J耦合分析，2个独立运行1-NS AI2^{使用了BMD模拟，并保存了10,000张快照。}然后， -从每个快照估算值。这³J（H_氮，h_±）耦合值是通过公式计算的（13）。

对于人工智能²BMD模拟在Chignolin上，我们首先将结构与106-µs的结构进行对齐，并全面地采样轨迹与初始结构对齐。然后，在原子坐标上使用时置的独立组件分析，用于将自由能景观投射到六维超级表面⁶¹。根据Minibatchk - 表示算法，我们聚集了所有构象，然后将60个折叠和展开的结构作为代表性结构。然后，对于每个结构，我们运行了10-NS AI²BMD和10-NS MM模拟。

在Ramachandran情节中， -是由C确定的二面角n_1,Nn_，cî±n和C_n， 和 _-是由n确定的二面角n，cî±n_,Cn和N_n+1_。下标代表蛋白质中残基的索引。_{根据基于每个箱中点的密度的玻尔兹曼分布来估计能量。该估计是利用平均力的势来进行的。} -和 -被视为两个反应坐标（x，y）。使用公式计算平均力值的潜力（14）。

其中\（{k} _ {{\ rm {b}}}} \）代表玻尔兹曼常数，时间是系统的温度（300 k）和\（g（x，{y}）\）表示归一化联合概率分布。图中显示的自由能值表示相对能量值，通过从观测值中减去最小自由能值来计算。这问得分是通过公式计算的（15）（参考²³）。

天然触点被定义为两个残基的重原子，这些残基至少由三个残基隔开，其距离小于天然构象中的4.5âã。等式（14）总和氮晶体结构中的一对天然接触；\（{r} _ {{ij}}}^{0} \）是沉重原子之间的距离我和原子j晶体结构中的天然接触\（{r} _ {{ij}}（x）\）是原子之间的距离我和原子j在构象中X。阈值问折叠和展开结构的值分别设置为> 0.82和<0.0323。^{对于快速折叠蛋白的自由能估计，我们首先在参考文献的模拟轨迹中均匀地采样了100,000点。}4。

折叠和展开状态通过相同的阈值分类^问先前研究中的值23。^{处于折叠状态的结构被聚集成10个簇。}根据MDTRAJ中的RMSD方法，根据Cî±坐标计算RMSD值。îG，根据折叠结构和展开的结构之间的比率计算折叠过程的自由能。使用重新评估的每种构象的能量，我们确定了蛋白质折叠的折叠焓和热容变化。从计算出的α推断熔化温度G，折叠焓和热容量变化。

为了计算蛋白质折叠和展开过程中焓和热容量的变化，110个残留的barnase（PDB：：1A2P）和84个残留CI2（PDB：2CI2）选择通过焓量扫描量热法和光谱法测量的焓和热容量值进行评估^36,37。对于每种蛋白质，除了来自 PDB 的折叠结构外，还生成了 20 个未折叠结构用于模拟。在先前的研究之后³⁵，每个构型都用10-ã水箱明确溶解。对于barnase，从折叠结构开始的20个平行模拟和20个从展开结构开始的模拟是由Gromacs 2018进行的，charmm36力场在phâ4.1处，温度为295 k，315 k和335âK.除了在Phâ6.3处进行模拟外，还适用了相同的设置，除了模拟，温度为335 k，350 -K和365 K.在NPT集合下进行了上述每种系统配置。通过AI计算从模拟采样的构象的势能值2^BMD。热展开后的焓变（H）计算为展开的合奏的平均焓与折叠合奏的焓之间的差异。然后，我们进行了线性回归以确定热容量的变化（C_p）从坡度以及熔化温度下的焓变。此外，我们还使用Gibbs的Helmholtz方程来估计折叠自由能。

在 pK_一个使用热力学集成确定，我们最初对琥珀色项目提供的仿真轨迹中的所有数据点重新加权（https://ambermd.org/tutorials/advanced/tutorial6/index.php）。随后，我们专注于轨迹的融合部分，每个窗口的2,500个数据点和硫氧还蛋白的每个窗口的500个数据点来计算平均能量值。îG是使用积分计算的：

其中w我”_{表示窗口宽度，}U表示内部能量，并且我”指定采样窗口。这种方法封装了不同质子化状态之间的自由化变化，促进了P的准确计算K_一个价值。

报告摘要

有关研究设计的更多信息可在 自然投资组合报告摘要链接到这篇文章。

AI的源代码和模型检查点²BMD仿真程序可通过GitHub获得https://github.com/microsoft/ai2bmd。参考

作者笔记

1. 这些作者做出了同等贡献：Tong Wang、Xinheng He、Mingyu Li、Yatao Li

2. 共同监督本工作的作者：王童、邵斌

作者和单位

1. 微软研究院，中国北京

   Tong Wang, Xinheng He, Mingyu Li, Yatao Li, Ran Bi, Yusong Wang, Chaoran Cheng, Xiangzhen Shen, Jiawei Meng, He Zhang, Haiguang Liu, Zun Wang, Shaoning Li, Bin Shao & Tie-Yan Liu

贡献

T.W.is the primary corresponding author.T.W.(primary) and B.S.led this study.T.W.(primary), B.S.and T.-Y.L.conceived the AI²BMD project.T.W.conceived and designed the end-to-end approach.T.Y.L.advised on this study.T.W., Y.L.and R.B. designed, accelerated, optimized and deployed the AI²BMD simulation program.T.W.designed the generalizable protein fragmentation approach.R.B., X.H.and M.L.implemented and optimized the generalizable protein fragmentation approach.M.L.and X.H.built the protein unit dataset.T.W., Y.W.and S.L.(in the early stage) designed and trained the AI²BMD potential.C.C., X.H.and M.L.implemented the polarizable solvent.X.H.and M.L.evaluated the accuracy of energy and force calculations.T.W., Y.L.and R.B. evaluated the time consumptions of energy and force calculations.Y.L.and X.S.conducted and analysed AI²BMD simulations for dipeptides.M.L.analysed theJcoupling values.Y.L.and X.S.conducted AI²BMD simulations for chignolin.X.S.analysed energy and force of chignolin simulations.J.M. analysed the RMSD and Ramachandran plot of chignolin simulations.X.H.and M.L.analysed the distance distributions from chignolin simulations.X.S., H.Z.和 T.W.conducted simulations and thermodynamic property analysis for two-state proteins.M.L.analysed thermodynamic properties for fast-folding proteins.X.H.conducted pK_一个分析。Z.W.participated in discussions in the early stage.T.W.写了手稿。B.S., H.L. and other authors revised the manuscript.所有作者都批准了手稿的最终版本。

通讯作者

通讯至王童或者邵斌。

利益竞争

作者声明没有竞争利益。

同行评审信息

自然thanks Yaoqi Zhou and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

开放获取本文获得 Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License 的许可，该许可允许以任何媒介或格式进行任何非商业使用、共享、分发和复制，只要您给予原作者适当的署名即可和来源，提供知识共享许可的链接，并指出您是否修改了许可材料。根据本许可，您无权共享源自本文或其部分内容的改编材料。The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.要查看此许可证的副本，请访问http://creativecommons.org/licenses/by-nc-nd/4.0/。转载和许可

关于本文