使用机器学习、深度学习和时间序列模型预测喜马拉雅山西北部海拔梯度的降雨量

气候变化对粮食安全的影响与其对农业的深远影响密切相关。由于气候变化的不可预测性造成普遍的不确定性，预测即将到来的种植季节的条件变得具有挑战性，这往往对农业活动不利¹。因此，农民和农业决策者在做出有关耕作、播种和管理作物的关键决策时，很大程度上依赖于他们对区域气候模式的了解。然而，在不断变化的气候中，传统方法变得不太可靠²。增强的气候预测为改善农业部门的决策带来了希望。这些先进的预报有可能减轻季风季节不佳或延迟等因素的不利影响，并提供利用预计有利天气条件的机会³。接受这些预测可以帮助农民和其他农业专业人士更有效地应对不确定性，保护他们的作物和产量，同时为适应气候变化的可持续农业实践奠定基础⁴。此外，强降水可能导致洪水，影响基础设施、交通网络和人类生计⁵。因此，如果能够提前量化一个地区的潜在降雨量，将有利于决策过程。预测降雨量对于提高农业产量和确保国家居民获得食物和清洁水至关重要⁶。

气候预测与农业之间的联系凸显了准确预测在塑造粮食安全未来方面的关键作用。近几十年来，改进降雨预报一直是科学界关注的焦点⁷。为了提高降雨预报的准确性，必须整合各种数据源并利用先进的建模技术。数值天气预报模型利用数学方程来模拟大气的行为以及与各种气候因素的相互作用。这些模型结合了历史数据、气象站的实时观测、卫星图像和复杂的计算算法⁸。降雨量与一系列气候因素有着错综复杂的联系，每一个因素都会影响其他因素，也受到其他因素的影响。这些因素包括最高和最低温度、大气压力、相对湿度和风速⁹。这些变量的相互关联性创造了一个复杂的系统，在维持整体气候平衡方面发挥着至关重要的作用。数值天气预报模型旨在通过检查气候要素和降雨之间的复杂关系来提供更精确的预报。大气的复杂性和不断变化的性质以及各种气候因素复杂的相互作用对降雨预报的改进提出了挑战。尽管在增强降雨预测技术方面取得了显着进展，但有几个因素仍然导致任务的复杂性。一个重大障碍是大气过程固有的不可预测性¹⁰。气氛充满活力和混乱，有突然的变化和意想不到的互动。这种不可预测性表明，即使初始条件发生微小变化，随着时间的推移也会导致截然不同的结果¹¹。这种现象对气象学家和气候科学家来说是一个巨大的挑战，他们致力于创建准确的模型来预测降雨模式。使降雨预报复杂化的另一个关键方面是需要长期历史数据来构建可靠的预测模型。历史数据帮助科学家识别降雨模式、趋势和周期。然而，获取全面、高质量的历史数据并不总是那么简单，特别是在监测基础设施有限的地区¹²。

降雨预测涉及复杂的随机和非线性行为，可以使用数据挖掘、人工智能 (AI)、ML 和 DL 等先进技术来解决。机器学习方法可以揭示历史降雨数据中的隐藏模式，并已被提议作为非线性和动态系统的替代建模方法⁵。因此，近年来，机器学习方法已成为降雨预测领域传统数据挖掘技术的有力继承者，这反映出人们对机器学习方法在应对预测降水模式的复杂挑战方面的能力的日益认可。^13,14,15,¹⁶。证明机器学习方法优于传统的降雨预测确定性方法。ML 模型的示例包括 RF、SVR 和 SVM。RF 采用决策树集合进行预测、提高准确性并处理复杂的数据关系^{17 号}。SVR 是一种适用于回归任务的 SVM，可以有效捕获数据中的非线性模式。SVM 是一种用于分类和回归的多功能模型，通过支持向量创建最佳决策边界¹⁸。

深度学习作为机器学习的一个子集，还展示了通过利用受人脑互连神经元启发的复杂神经网络来增强预测能力的巨大潜力¹⁹。深度学习技术涵盖了人工神经网络的各种算法。这些网络由互连的节点层或“神经元”组成，每个层都处理和转换输入数据，然后将其传递到下一层。这些网络的深度和复杂性使它们能够捕获广泛数据集中的复杂模式和关系。这种能力在以高维和非线性数据为特征的领域尤其有价值，例如气候科学和气象学²⁰。深度学习方法与传统的机器学习方法密切相关，尽管在架构复杂性和特征提取层次上有所不同²¹。虽然深度学习和传统机器学习都致力于识别数据模式，但深度学习模型擅长在多个抽象级别自主学习数据表示。这意味着深度学习模型可以自动发现原始数据中的复杂特征，而无需显式特征工程，这通常需要领域专业知识并且可能非常耗时²²。深度学习在降雨预测中的应用涉及根据历史气候数据训练神经网络。这些网络旨在识别关键变量之间的隐藏相关性、非线性关系和时间依赖性，以实现准确的降雨预报²³。当神经网络处理这些数据集并从中学习时，它们会完善其内部表示，从而逐渐使它们能够做出越来越准确的预测。深度学习方法有效地利用了降雨预报中气候因素的相互关联性，考虑了温度、湿度、风速和气压等多种变量，并认识到它们对降雨模式的综合影响²⁴。这种综合方法比传统方法具有优势，传统方法可能难以捕捉这些变量之间复杂的相互作用。此外，DL 处理大量数据的能力非常符合气象预报的要求，其中历史气候记录跨越数十年并包含一系列变量。深度学习模型能够识别这些数据集中的微妙趋势、非线性依赖性和复杂的时间模式，从而可以实现更准确、更可靠的降雨预测²⁵。

深度学习方法的示例包括 ANN、RNN、KNN 和 GRU。人工神经网络模拟互连的神经元来捕获数据中的复杂关系，从而增强学习能力。RNN 专门研究序列建模，为语言处理等任务保留先前输入的记忆²⁶。KNN 是一种根据特征空间中数据点的接近程度进行预测的学习算法。GRU 是 RNN 的一种变体，解决了 RNN 中的梯度消失问题并改进了远程依赖性捕获^{27 号}。此外，还有 ARIMA、LSTM、三角函数、Box-Cox 变换、ARMA 和 TBATS 模型等时间序列模型。这些模型允许数据分析师跨各种应用程序对时间序列数据进行建模和预测。例如，ARIMA 将自回归和移动平均组件与差分相结合以处理非平稳数据。LSTM 是一种 RNN，可以捕获序列中复杂的时间关系^28,29。三角模型利用正弦函数来捕获循环模式，这对于具有周期性波动的数据来说是理想的选择。Box-Cox 变换稳定方差并增强数据的正态性³⁰。ARMA 模型融合了自回归和移动平均成分，而 TBATS 考虑了复杂的趋势和季节性模式^{17 号}。使用线性回归作为机器学习方法旨在通过建立与其他大气变量的关系来预测降雨量^31,3233。进行了彻底的比较研究，以评估统计模型和回归技术在利用环境特征预测降雨量方面的有效性。该研究强调了回归技术在预测降雨模式时优于统计模型的性能。此外，他们的调查表明，与 SVM 和决策树方法相比，RF 模型在 ML 算法中表现出更高的预测准确性。这项研究为降雨预测提供了宝贵的见解，揭示了特定建模方法的优势。DL LSTM 模型已被证明对于降雨预测是有效的。印度海得拉巴地区降雨预报研究^20,34等人提出了一种增强的 LSTM 模型，并将其与 Holt-Winters、ARIMA、极限学习机 (ELM) 和 RNN 等其他模型进行了比较。使用ANN预测月平均降雨量验证了结果³⁵。研究结果表明，在三种不同类型的网络（层循环、级联前馈反向传播和前馈反向传播）中，前馈反向传播网络类型产生了最佳结果。

先前的研究利用线性回归模型来确定预测降雨的关键特征，包括太阳辐射、可检测到的水蒸气和日常模式³⁶。研究发现，温度、风和气旋可以用来预测农业部门增长的降雨量，农民可以据此做出决定。一些研究人员还利用温度、相对湿度、压力和风速等大气特征，使用 ANN、RF 和多元线性回归模型等机器学习技术来准确预测降雨量^37,38。因此，机器学习、深度学习和时间序列建模的结合代表了一个有希望的前沿领域，可以增进我们对气候模式的理解并提高我们预测降雨的能力。

本研究的重点是探索喜马拉雅山西北部的降雨数据，有几个关键目标。首先，我们的目标是评估先进的机器学习算法在预测降雨模式方面的有效性。其次，我们寻求评估专门针对该地理区域定制的深度学习模型的准确性。第三，我们打算将机器学习和深度学习方法的性能与气象预测中常用的传统时间序列技术进行比较。此外，我们的研究旨在分析海拔变化如何影响这些预测模型的精度。最后，根据我们的研究结果，我们的目标是提出一种整体方法来提高该地区降雨预测的整体准确性。通过这些目标，我们旨在贡献宝贵的见解，以促进山区气象预报的科学理解和实际应用。这项研究采用多维方法来揭示该地区降水趋势的复杂性，该地区因其复杂的海拔依赖气候变化而闻名。通过整合这些创新方法，我们的目标是解码环境因素与降雨之间的复杂关系，最终开发出更准确和本地化的预测模型。

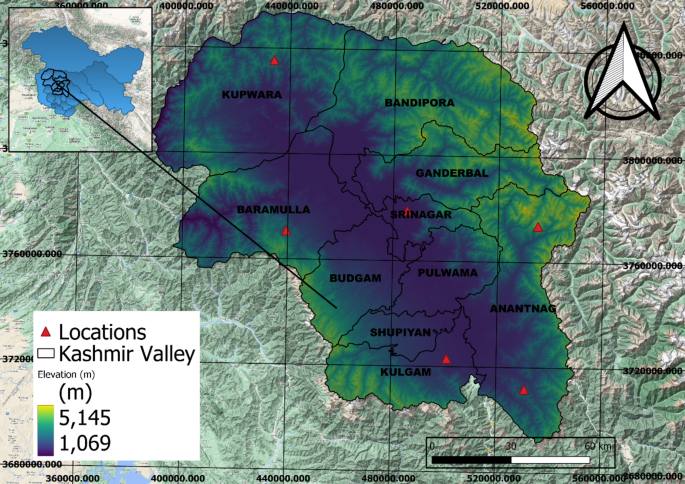
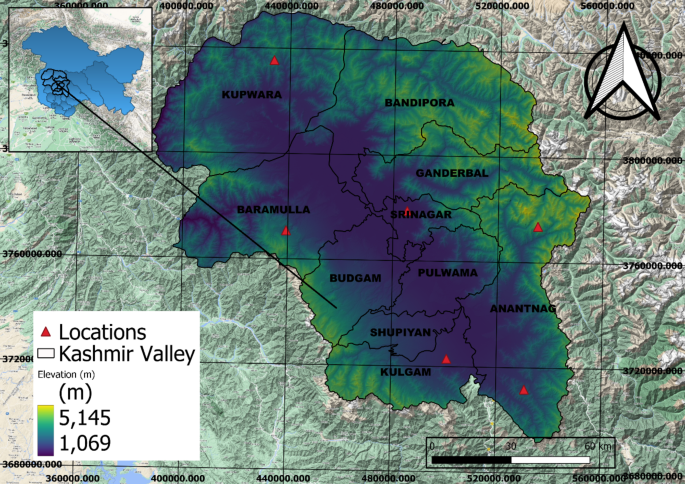
案例研究区域、气象数据和预处理。研究区域覆盖印度喜马拉雅山西北部地区，中心位置约为北纬33°5°24°240°，东经74°47°24°24°2。图 1说明了所覆盖的研究区域的位置。研究地图由QGIS 3.30.0生成。六个气象站位置分布在地图上的海拔梯度上。主要数据是从印度气象部 (IMD) 总部收集的。该数据集包含 40 年（1980 年至 2020 年）最高和最低气温以及降雨量的每日数据。初始数据预处理阶段涉及多项任务：数据转换、处理缺失值、编码分类变量以及将数据集划分为训练集和测试集。由于原始数据同时显示缺失值和极值或异常值，因此采取了纠正措施。缺失值被替换为不可用 (N.A)。随后，数据集在准备进行实验之前经历了编码过程。确定并隔离了对降雨预测至关重要的相关属性。然后对数据集进行划分，其中 80% 指定用于训练，20% 用于测试，作为模型的输入。

研究区域地图（地图是使用QGIS 3.30.0创建的https://www.qgis.org/）。

型号

本研究的重点是通过机器学习、深度学习和时间序列方法的组合方法进行降雨预测。该分析涵盖三种不同的 ML 算法：ANN、SVR 和 RF；三种深度学习算法：RNN、LSTM、GRU；以及两种时间序列算法：ARIMA 和 TBATS。这些不同的算法利用了与降雨量中度到强相关的输入变量，这些变量取自多个环境因素。模型参数和有关模型的信息在补充表中给出 1秒。该研究通过使用 RMSE 和 MAE 指标评估性能来确定并报告最有效的模型和算法，表中给出了各种模型在不同海拔高度的其他精度评估，例如 Bias 和 R2 1秒。

机器学习 (ML) 算法

使用三种机器学习算法根据数据集的行为来预测降雨量。下面讨论这些算法：

人工神经网络（ANN）

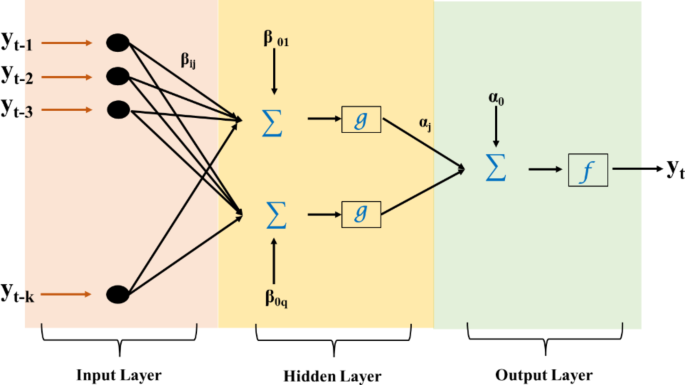
ANN 是一种受大脑结构和功能启发的机器学习模型。人工神经网络的架构通常由输入层、一个或多个隐藏层和输出层组成。输入层接收输入数据并将其传递到隐藏层。隐藏层使用权重和偏差将输入数据转换为更适合任务的新表示。输出层根据隐藏层处理的信息产生最终预测。权重和偏差是在训练过程中学习的，使模型能够做出越来越准确的预测。隐藏层的数量、隐藏层的大小和使用的激活函数决定了模型的容量及其学习输入和输出之间复杂关系的能力。如图所示 2,\({y}_{t}\)被视为其滞后值的函数\(\:{y}_{t-1},{y}_{t-2},\点\:,\:{y}_{t-k}\)以及各自的权重。

ANN 的模型架构。

在哪里\(\:{a}_{j}\:(j=\text{0,1},2,\点\:,q)\)和\(\:{\beta\:}_{ij}\:(j=\text{0,1},2,\dots\:,q;i=\text{1,2},.,k)\)是模型的连接权重；k是输入层中的节点数，q是隐藏层中的节点数。

支持向量回归（SVR）

SVR，由 Vapnik 等人开发。³⁹，是一种用于回归和时间序列问题的 ML 模型。SVR模型架构由以下组件组成。首先，使用核函数（例如径向基函数（RBF）或多项式函数）将输入特征变换到高维空间。转换后的特征用于训练模型。该模型通过最大化数据点和边界之间的余量来找到最佳边界。使用惩罚偏离目标值的成本函数来估计模型参数。该模型通过将特征转换到高维空间并应用线性回归模型来对新的输入数据进行预测。核函数和正则化参数 (C) 是超参数，可以通过调整来提高模型的性能。SVR模型的主要优点是它可以使用合适的核函数处理输入和输出之间复杂的非线性关系。

随机森林 (RF)

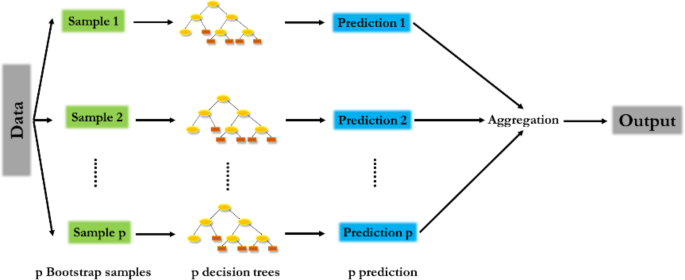
RF 是一种基于决策树的 ML 算法。它构建多个决策树并结合它们的预测来提高模型的整体准确性和稳定性。许多决策树都是根据随机选择的训练数据子集进行训练的。每个决策树都经过训练，通过根据输入特征的值将数据递归地划分为子集来对目标变量进行预测。新输入样本的最终预测是所有决策树做出的预测的平均值。每次分割时随机选择特征有助于去相关树并减少过度拟合。用于训练每棵树的引导训练数据样本有助于减少预测方差。RF模型的架构如图1所示。 3。

射频架构。

深度学习 (DL) 算法

为了根据当前环境数据估计每日降雨量，选择了 RNN、LSTM 和 GRU 三种特定算法进行实证研究。因此，对这三种深度学习算法进行了测试和并列，以确定预测每日降雨量的最佳方法。

循环神经网络（RNN）

RNN 是处理顺序数据的深度学习模型。它有一个反馈循环，允许信息从一个序列步骤传递到下一个序列步骤。RNN 的核心架构由一个具有隐藏状态的重复模块组成，该模块存储有关前一时间步的信息，以及一个输入到隐藏层，该层将当前输入和最后一个隐藏状态作为输入并输出当前隐藏状态状态。然后，隐藏状态用作隐藏到输出层的输入，该层生成当前时间步的输出。输入到隐藏层和隐藏到输出层的权重在所有时间步骤中共享，允许模型学习序列数据中的模式。RNN 模型的内部结构可以使用以下方程描述：

输入层：输入层接收表示为x(t)的输入序列，其中t表示时间步长。

隐藏层：隐藏层包含使用以下方程计算隐藏状态 h(t) 的循环神经元：

其中，f 是激活函数（例如 tanh），\(\:{\text{W}}_{hx}\)是输入到隐藏层连接的权重矩阵，\(\:{\text{W}}_{hh}\)是隐藏层到隐藏层连接的权重矩阵，并且\(\:{\text{b}}_{h}\)是偏置向量。

输出层：输出层使用以下方程计算输出 y(t)：

在哪里，\(\:{\text{W}}_{hy}\)是隐藏层到输出层连接的权重矩阵，并且\(\:{\text{b}}_{y}\)是偏置向量。

这些方程描述了简单 RNN 模型的基本结构。更复杂的 RNN 模型可能具有额外的层或使用不同类型的激活函数或循环神经元。该架构可以扩展多个隐藏层以形成深度 RNN 或多个隐藏状态以创建 LSTM 或 GRU。

长短期记忆（LSTM）及其变体

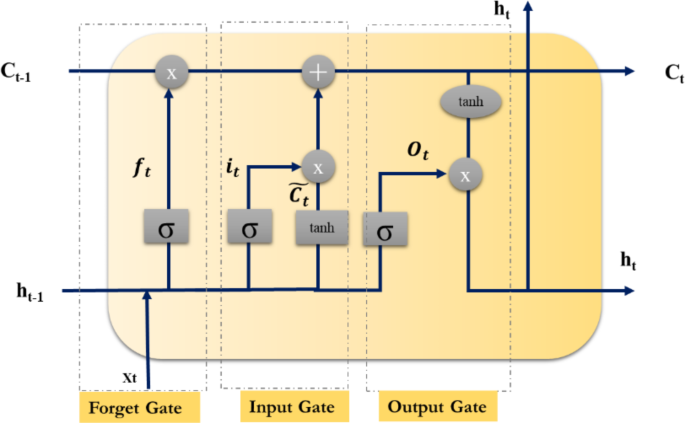
LSTM 是一种 RNN 类型，广泛用于处理时序数据，例如时间序列、语音信号和文本。它是由⁴⁰作为传统 RNN 中出现的梯度消失问题的解决方案。LSTM模型是一种RNN类型，可以长时间记住之前的输入。LSTM 网络的架构由记忆单元、输入门、遗忘门和输出门组成。存储单元负责长期存储信息，而门则控制信息进出存储单元的流动。输入门控制进入记忆单元的信息流，允许网络决定保留哪些信息。遗忘门根据当前输入和之前的记忆状态决定应该丢弃哪些信息。输出门根据当前输入和之前的记忆状态决定应该输出什么信息。LSTM单元的结构如下图所示： 4和方程：

LSTM 单元的结构。

输入门：控制允许进入细胞状态的新信息量。它是使用以下等式计算的：

在哪里，\（\：{它}\）是时间步的输入门\(\:t\),\(\:{W}_{i}\)是权重矩阵，\(\:\:{h}_{t-1}\)是先前隐藏状态的串联\(\:t-1\:\)和当前输入\(\:{x}_{t}\)， 和\（\：{双}\：\）是偏置项。sigmoid 激活函数\(\:\西格玛\:\)确保输入门在 0 和 1 之间。

遗忘门：控制从细胞状态中遗忘的信息量。它是使用以下等式计算的：

在哪里，\(\:\:{f}_{t}\)是时间步的遗忘门\(\:t\),\(\:{W}_{f}\)是权重矩阵，并且\(\:{b}_{f}\)是偏置项。

单元状态：模型的连续记忆，存储过去的信息。它使用以下等式进行更新：

在哪里，\(\:{C}_{t}\)是时间步的细胞状态\(\:t\),\(\:{f}_{t}\)是遗忘门，\（\：{它}\）是输入门，\(\:{C}_{t-1}\)是之前的细胞状态，并且\(\:\stackrel{\sim}{{C}_{t}}\)是候选细胞状态，计算如下：

\（\：{厕所}\）和\（\：{公元前}\）是候选人输入的权重和偏差。

输出门：控制从单元状态输出到隐藏状态的信息量。它是使用以下等式计算的：

在哪里，\(\:{o}_{t}\)是时间步的输出门\(\:t\),\(\:{W}_{o}\)是权重矩阵，并且

\(\:{b}_{o}\)是偏置项。

隐藏状态：模型当前状态的表示。它是使用以下等式计算的：

在哪里，\(\:{h}_{t}\)是时间步的隐藏状态\(\:t\),\(\:{o}_{t}\)是输出门，并且\(\:{C}_{t}\)是细胞状态。

上述方程构成了 LSTM 单元的核心，多个单元可以堆叠在一起以创建多层 LSTM 网络。深度 LSTM 模型是 LSTM 模型的变体，具有多层 LSTM 单元。双向 LSTM 以两种方式处理输入序列：前向（从开始到结束）和后向（从结束到开始）。

门控循环单元 (GRU)

GRU 是 RNN 模型的改进版，具有两个门：重置门和更新门。这些门有助于调节信息流并防止传统 RNN 中可能出现的梯度消失问题。GRU 的架构类似于 LSTM 网络，但参数较少。

时间序列算法

选择 ARIMA 和 TBATS 使用实时环境数据来预测每日降雨强度。对这些算法进行了测试和比较，以确定准确的每日降雨量预测的最佳方法。

自回归综合移动平均线 (ARIMA)

ARIMA 是一种流行的时间序列预测算法，用于对单变量数据进行建模和预测。对于 ARIMA 模型，时间序列数据必须是平稳的，这意味着其均值、方差和协方差随时间保持恒定。如果数据不平稳，则应用差分步骤使其平稳。ARIMA 模型是根据 p、d 和 q 的值来选择的，其中 p 是 AR 项的数量，d 是应用的差分步骤的数量，q 是 MA 项的数量。自相关函数 (ACF) 和偏自相关函数 (PACF) 用于识别时间序列数据中的模式，并确定要包含在 ARIMA 模型中的自回归 (AR) 和移动平均 (MA) 项的数量。使用最大似然估计或其变体将该模型拟合到时间序列数据。使用残差分析并将预测值与预留用于验证的时间序列数据的一部分的实际值进行比较来验证模型。ARIMA 模型预测时间序列数据的未来值。

具有 Box-Cox 变换、ARMA 误差、趋势和季节性分量 (TBATS) 的指数平滑状态空间模型

TBATS 是一种针对单变量时间序列数据的时间序列预测算法。它是一种结合了指数平滑和 ARIMA 模型的混合算法，适合对季节性、趋势和不规则性等复杂时间序列模式进行建模。该算法将时间序列建模为多个分量的组合，包括趋势、季节性分量和不规则分量。该算法使用最大似然估计来估计模型参数，并通过组合不同元素来预测未来值。人们发现 TBATS 在各种时间序列数据集上表现良好，包括具有多种季节性模式、非平稳趋势和不规则波动的数据集。

统计评价

一般来说，有必要评估已开发的预测模型的性能，并使用特定的统计措施将其与其他模型进行比较。然而，采用多个统计指数至关重要，因为不同的模型可能会为特定指数产生相似或几乎相同的值。这种相似性使得确定哪个模型比其他模型表现更好变得具有挑战性。每个统计指标从单一角度评估模型的性能，即模型的输出与期望值的匹配程度。因此，建议跨多个统计指标评估模型，全面评估每个模型的性能并进行稳健的比较分析，最终确定最合适的建模方法。通常使用两个性能指标来评估预测模型的有效性：RMSE 和 MAE。RMSE 衡量预测值与实际值之间误差的平均大小。RMSE 值越低表示模型精度越高，因为它们表示预测数据点和观测数据点之间的差异较小。类似地，MAE 量化预测值和实际值之间的平均绝对差，值越低表示预测越准确。RMSE 和 MAE 可以定义为

在哪里\(\:{\text{Y}}_{\text{t}}\)是实际值，\(\:\widehat{{\text{Y}}_{\text{t}}}\)是拟合值，n 是观测值的数量。

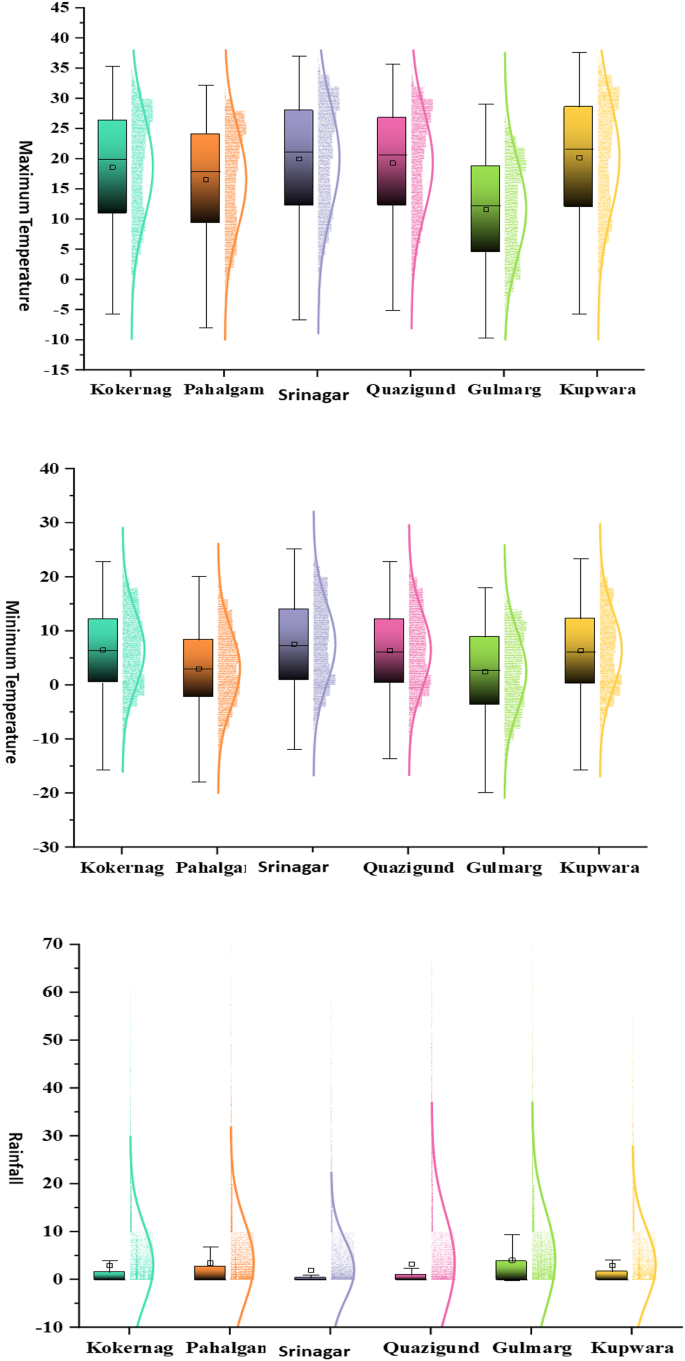
喜马拉雅山西北部海拔梯度的温度描述性统计揭示了显着的变异性，这对于了解当地气候动态及其对降雨模式的影响至关重要。L1 至 L6 位置的平均最高温度范围为 11.65 至 20.21℃，反映了受海拔高度影响的不同热状况（表 1）。这些发现与之前强调海拔在温度变化中的作用的研究一致⁴¹。最高温度值范围广泛，从 5.70 ℃ 到 37.60 ℃，揭示了研究区域内广泛的气候谱，表明高山和低海拔气候。同样，同一地点的平均最低气温在 2.50 到 7.64 ℃ 之间，这表明与地势较低的地区相比，海拔较高的地区气候凉爽（表 2）。该梯度对于理解蒸散量和降水形成等与温度相关的过程至关重要⁴²。最高和最低温度的标准误差和偏度值进一步阐明了分布特征，表明温度数据分布存在轻微的不对称性，但变异性相对较低，表明测量的稳健性^34,43,44。这些温度统计数据是预测该地区降雨模式的基础框架。研究表明，温度梯度直接影响大气稳定性、水分含量和降水事件的发生^45,46,47,48。通过将特定海拔温度数据整合到降雨模型中，研究人员可以提高针对山区的预测模型的准确性⁴⁹。

对喜马拉雅山西北部不同海拔位置（L1 至 L6）降雨模式的分析为了解山区降水建模相关的空间变化和预测挑战提供了宝贵的见解。平均降雨量范围从 1.94 到 4.09 毫米，说明相对较小的地理距离内降水水平存在显着差异（表 3）。每个地点观测到的最小和最大降雨量的广泛范围进一步强调了这种变化，反映了地形、大气动力学和当地气候条件的复杂相互作用。标准误差和偏度值为降雨数据的分布特征提供了额外的视角。较高的偏度值（例如在 L2、L3、L4 和 L5 位置观察到的偏度值）表明分布不对称，有极端降雨量较高或较低的趋势，可能受到局部天气现象（如地形抬升或对流过程）的影响^44,50。相反，较低的偏度值表明降雨分布更加对称，表明降雨模式更加温和和一致^51,52,53,54。应用机器学习模型（RF、SVR、ANN 和 KNN）根据气象变量预测降雨量揭示了不同海拔梯度上不同的模型性能。RF 和 SVR 模型在训练和测试阶段通常表现出较高的 RMSE 值，这表明在山区捕获预测变量与降雨结果之间复杂的非线性关系方面存在挑战。这些发现与之前的研究一致，强调统计模型对空间异质性的敏感性以及山区需要稳健的验证策略^55,56,57。相比之下，ANN 和 KNN 模型表现出相对较低的 RMSE 值，表明它们有潜力更好地捕捉不同海拔地区降雨模式的空间变化和非线性。这些模型的卓越性能可能源于它们学习气象数据中固有的复杂模式和关系的能力，包括地形影响和微气候变化等与海拔相关的因素^58,59。这些发现凸显了整合特定海拔气象数据和采用先进建模技术来提高山区降雨预报准确性的重要性。未来的研究方向可能包括通过纳入额外的环境变量（例如地形特征、植被覆盖）来完善模型输入，并探索集成建模方法以减轻与单个模型性能相关的不确定性^{60,61,62,63,64}。此外，结合高分辨率卫星数据和地面观测可以进一步改善降雨模式的空间表示，并支持复杂地形环境中更稳健的模型验证。

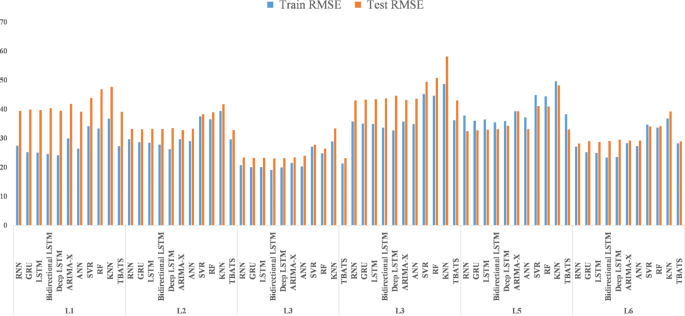
应用机器学习、深度学习和时间序列建模技术根据喜马拉雅山西北部海拔梯度的气象变量来预测降雨量，为模型性能和预测准确性提供了宝贵的见解（表 4）。RF、SVR、ANN 和 KNN 等 ML 模型表现出不同水平的有效性，如它们在不同海拔高度（L1 至 L6）的训练和测试 RMSE 值所示（图 1）。 5）。这些差异强调了这些模型对气候条件空间变化以及气象预报与降雨模式之间复杂相互作用的敏感性。深度学习模型（包括 LSTM、双向 LSTM、深度 LSTM、GRU 和 RNN）也表现出了跨海拔梯度的不同 RMSE 值。这些模型利用数据中的顺序依赖性，并在捕获气候变量中的时间模式和非线性关系方面显示出前景，这对于动态山区环境中准确的降雨预测至关重要^40,65。此外，ARIMA 和 TBATS 等时间序列建模方法可以深入了解不同海拔高度降雨量的时间变化。这些模型表现出不同的训练和测试 RMSE 值，反映了它们捕获降雨数据的短期波动和长期趋势的能力^56,66,67,68。在这些建模技术中观察到的 RMSE 值的差异凸显了选择适当方法来解释山区固有的复杂空间和时间动态的重要性。一些模型中较高的 RMSE 值表明准确捕捉局部尺度变化和极端天气事件面临挑战，这对于山区生态系统的有效水资源管理和备灾至关重要^69,70,71。整合不同的建模方法并利用先进的统计技术增强了我们对山区降雨变化的理解。

跨海拔梯度的 RMSE 条形图。

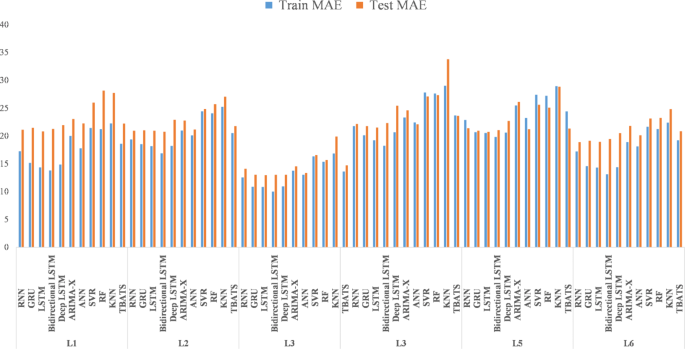
深度学习模型（包括 LSTM、RNN、双向 LSTM、深度 LSTM 和 GRU）在各个研究地点表现出不同程度的有效性。LSTM 始终表现出强大的性能，在多个实例中与其他深度学习模型相比实现了更低的 RMSE 和 MAE³⁰。例如，在位置 1，LSTM 的训练 RMSE 为 26.4051，测试 RMSE 为 38.2848，表明它能够熟练地捕捉温度变量和降雨模式之间的复杂关系。双向 LSTM 还表现出有竞争力的性能，尤其值得注意的是其在多个位置的 MAE 分数较低。然而，与 LSTM 相比，它显示出略高的 RMSE 值，这表明不同评估指标的预测准确性存在潜在差异。另一方面，Deep LSTM 和 GRU 虽然通常表现良好，但与 LSTM 和双向 LSTM 相比，表现出更高的 RMSE 和 MAE 值（图 1）。 6）。这一观察结果表明，这些模型可能更难以捕捉喜马拉雅山西北部地区特有的温度与降雨关系的复杂细微差别。相比之下，传统的 ML 模型（例如 ANN、KNN、SVR、RF 和时间序列方法 ARIMA）在所有位置始终表现出较高的 RMSE 和 MAE 值⁷²。具体来说，KNN、SVR 和 RF 表现出明显更高的误差指标，突显了与 DL 模型相比，它们在准确捕获降雨预测任务固有的非线性依赖性方面的局限性。

MAE 沿海拔梯度的条形图。

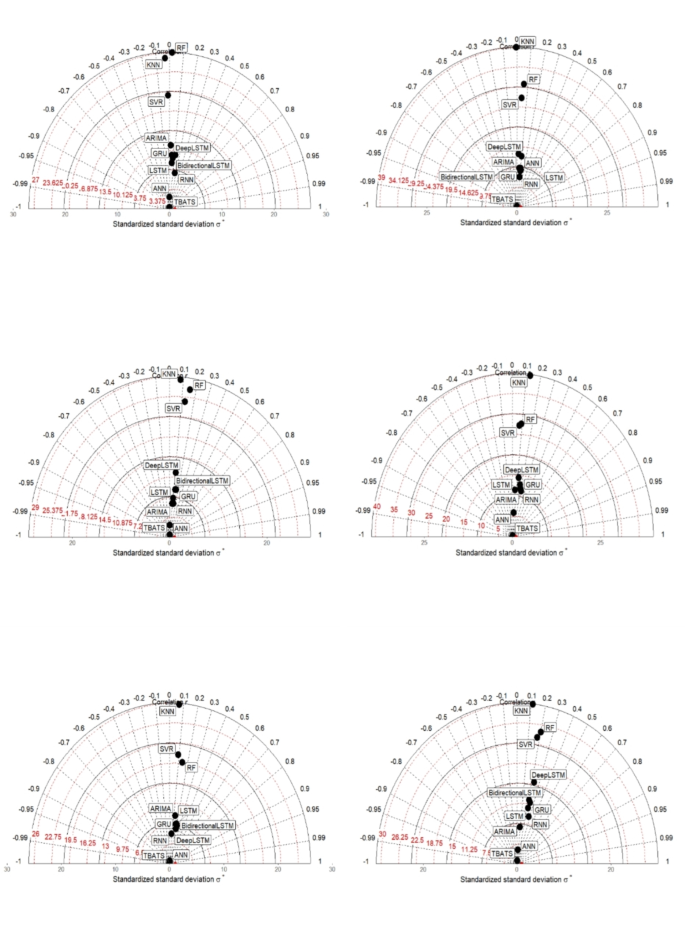
在所有六个检查地点，深度学习模型的表现始终优于机器学习和时间序列模型（图 1）。 7）。具体来说，LSTM 和双向 LSTM 成为表现最好的模型，分别在位置 L1 到 L6 上实现了最低的 RMSE 和 MAE 分数。同时，RNN、LSTM、双向 LSTM 和深度 LSTM 因其在相同位置的测试 MAE 方面的性能而被确定为优秀模型。总体而言，DL 算法表现出卓越的准确性，其中双向 LSTM 显示出最高的有效性，其次是 LSTM、RNN、Deep LSTM 和 GRU（按降序排列）。相比之下，ML 模型的表现相对优于传统时间序列方法，其中 ANN 领先，其次是 KNN、SVR 和 RF。以 TBATS 和 ARIMA 为代表的时间序列模型精度排名最低（图 2）。 8）。DL 模型在预测喜马拉雅山西北部降雨模式时的偏好可归因于几个因素。首先，数据的复杂性和非线性性质，受海拔变化、地形和大气稳定性的影响，给机器学习和时间序列模型准确捕捉这些关系带来了挑战⁷³。DL 模型（例如 LSTM 和双向 LSTM）专门设计用于通过自动学习复杂的数据模式来处理此类复杂性^{27 号,72}。此功能减少了对手动特征工程的需求，并通过有效管理降雨和温度数据中固有的噪声来提高预测准确性。深度学习模型受益于该地区大型历史数据集的可用性，这对于有效训练这些模型至关重要。广泛的数据使深度学习模型能够很好地泛化，并针对数据的时间变化保持鲁棒性，从而提高整体预测准确性。这项研究通过将先进的机器学习（ML）和深度学习（DL）技术应用于降雨预测，为克服农业规划和气候适应方面的挑战做出了重大贡献。由于传统的预测方法与日益不可预测的气候作斗争，这项研究通过复杂的算法提高了预测的准确性，使农民和农业规划者能够做出更明智的决策。通过整合复杂的气候数据并评估喜马拉雅山西北部的模型有效性，该研究为提高预测精度和管理不同的环境条件提供了重要的见解。这一进步支持在气候变化的情况下更好的农业实践、基础设施发展和整体粮食安全。

天气变量在海拔梯度上的分布。

比较模型精度的高度泰勒图。

正如本研究所述，使用先进的机器学习 (ML) 和深度学习 (DL) 技术进行降雨预测代表了气象预报的重大进步，对工程师和利益相关者具有重要意义，特别是在半干旱地区。随机森林 (RF)、支持向量回归 (SVR)、长短期记忆 (LSTM) 和门控循环单元 (GRU) 等技术显着提高了降雨预测的准确性。这种精度的提高对于依赖季节性降雨的地区的有效规划和管理至关重要。然而，在实践中应用这些技术会带来一些考虑。一个关键问题是平衡模型的准确性和复杂性。虽然这些先进方法可以提供高度准确的预测，但它们也带来了更高的计算需求和复杂性。工程师和利益相关者必须评估提高准确性的好处是否足以应对与实施和维护这些复杂系统相关的挑战。这些模型需要强大的计算能力和专业知识，这对于技术资源有限的地区来说可能是一个障碍。有必要将这些先进模型正确集成到现有的预测系统中，以确保准确性的提高满足运营需求。另一个重要的考虑因素是对广泛且高质量数据集的依赖。这些先进模型在处理大量数据时表现最佳，而这些数据可能并不总是可用，特别是在气象信息稀疏的地区。这表明需要更好的数据收集基础设施。工程师应重点关注增强数据采集系统并制定处理有限数据的策略，以充分利用这些预测技术。

这些方法对湿度、风速和太阳辐射等其他气象变量的适应性也很重要。虽然这些方法背后的原理是通用的，但每种气候变量都有独特的挑战，可能需要专门的方法。尽管用于降雨预测的方法可以扩展到其他变量，但工程师需要根据每个特定情况定制模型，以确保准确性和有效性。运营整合是另一个实际挑战。将这些先进模型纳入现有的农业规划、灾害管理和基础设施发展系统需要仔细考虑。利益相关者必须解决如何将这些模型整合到实际决策过程中，这不仅包括技术适应，还包括用户的培训和能力建设。确保人员接受适当的培训以使用这些先进工具对于最大化他们的利益至关重要。改进降雨预报的好处是相当大的。预测精度的提高可以实现更好的农业规划，例如更精确的灌溉调度和有效的水资源管理。它还通过帮助工程师创建能够抵御极端天气事件的基础设施来支持基础设施设计和灾难准备。对于政策制定者来说，先进的预测技术为制定数据驱动的政策奠定了基础，以促进可持续资源管理和增强气候适应能力。总之，虽然先进的降雨预测技术具有相当大的优势，但它们还需要仔细管理模型复杂性、数据需求和操作集成。有效应对这些挑战可以显着改善决策、基础设施规划和政策制定，最终支持气象及相关领域更具弹性和可持续的实践。模型参数如表所示 2S。

作者和单位

1. 克什米尔谢尔克什米尔农业科技大学 (SKUAST-K) 农业学院瓦杜拉农学部，查谟和克什米尔，193201，印度

   奥瓦伊斯·阿里·瓦尼 & 赛义德·谢拉兹·马赫迪

2. ICAR-印度农业统计研究所，新德里，110 012，印度

   马里兰州耶辛

3. 农业与水道部 (MOA & W) 农学部（块根作物），Suva City, 679, Fiji

   沙马尔·沙桑·库马尔

4. 利物浦约翰摩尔斯大学生物与环境科学学院，利物浦，L3 3AF，英国

   亚历山大·S·加格农

5. VIT-AP 大学高级科学学院数学系，印度安得拉邦伊纳沃卢，522237

   费赞·丹麦语

6. 土木、环境和自然资源工程，吕勒奥理工大学，97187，吕勒奥，瑞典

   纳迪尔·安萨里

7. 沙特国王大学食品与农业科学学院植物生产系，P.O.Box 2460, 利雅得 11451, 沙特阿拉伯

   萨拉赫·埃尔·亨达维

8. 沙特国王大学农业工程系，食品与农业科学学院，P.O.Box 2460, 利雅得 11451, 沙特阿拉伯

   穆罕默德·马塔尔

9. 雨养农业先进中心 (ACRA)，Dhiansar, Bari-Brahmana-181133, SKUAST-Jammu, UT-J&K, 印度

   赛义德·谢拉兹·迈赫迪

贡献

概念化、监督、方法论、形式分析、写作——初稿准备、写作——审查和编辑、O.A.W.、S.S.M.、M.Y.、S.S.K.、A.S.G.；数据管理、项目管理、调查、写作审查和编辑、F.D.、N.A.-A.、S.E.-H.、M.A.M.所有作者均已阅读并同意稿件的出版版本。

通讯作者

通讯至赛义德·谢拉兹·迈赫迪,纳迪尔·安萨里或者穆罕默德·马塔尔。道德宣言

作者声明没有竞争利益。

附加信息

施普林格·自然对于已出版的地图和机构隶属关系中的管辖权主张保持中立。

电子补充材料

本文根据知识共享署名 4.0 国际许可证获得许可，该许可证允许以任何媒介或格式使用、共享、改编、分发和复制，只要您对原作者和来源给予适当的认可，并提供链接到知识共享许可证，并指出是否进行了更改。本文中的图像或其他第三方材料包含在文章的知识共享许可中，除非材料的出处中另有说明。如果文章的知识共享许可中未包含材料，并且您的预期用途不受法律法规允许或超出了允许的用途，则您需要直接获得版权所有者的许可。要查看此许可证的副本，请访问http://creativecommons.org/licenses/by/4.0/。转载和许可

关于本文