使用基于 Pyiron 的自动化工作流程从电子到具有机器学习潜力的相图

机器学习原子间势 (MLP) 的出现正在彻底改变计算材料科学领域，使大型系统和复杂材料特性的模拟能够从头开始准确^1,2,3,4,5。然而，这些数据驱动的原子间势的开发是一项计算密集型任务，需要自动化且可靠的工作流程。

MLP 开发的生命周期大致可分为以下任务：(i) 生成包含参考数据的数据库，(ii) 将模型参数拟合到参考数据，以及 (iii) 验证指定范围的参数化结果。特性。此外，通常需要通过主动学习方法在任务之间提供反馈循环，以确定可迁移性^6,7。

设置参考数据库的初始任务通常需要对尽可能完整地跨越感兴趣的配置空间的广泛原子环境执行数千次密度泛函理论 (DFT) 计算。现在可以使用通用工作流程框架来促进此类计算^8,9,10,11或专门为特定 MLP 类设计的工具^{12,13,14,15,16,17 号}。尽管如此，仍然缺乏标准化的工作流程设置、计算元参数和结构数据库。因此，每个研究小组主要依靠自己的专业知识和经验。这不仅可能导致生成的数据不一致（例如，由于 DFT 设置的变化，例如交换相关函数、布里渊区采样或平面波截止）^18,19，但它也可能强烈限制来自不同来源的数据交换以及将其收集到更大的数据库中。

当谈到 MLP 开发的第二阶段时，即拟合模型参数，情况仍然相似。许多优化算法和软件工具都是针对特定类别的潜力而定制的，并且不易转移。因此，研究人员不仅必须确定适合感兴趣的系统的适当类型的潜力，而且通常需要学习各种特定的软件工具，每个工具都使用自己的术语。

开发周期的最后任务是对拟合参数化进行彻底验证。应该强调的是，势的预测和参考 DFT 数据之间的简单相关性，例如对于能量和力来说，在大多数情况下是不够的，甚至可能会产生误导。至关重要的是，不仅要评估基本物理特性（例如能量体积曲线、弹性模量或声子谱），还要在有限温度下进行动态模拟，以检查模型在训练域之外的杂散行为。现有举措^20,21,22主要关注经典原子间势，而 MLP 的自动验证仍然很少²³。这使得用户很难确定其应用的特定 MLP 参数化的安全应用范围。在将模型应用于复杂材料特性的模拟（例如扩展缺陷、相变或相图预测的研究）之前，彻底的验证也是必不可少的。

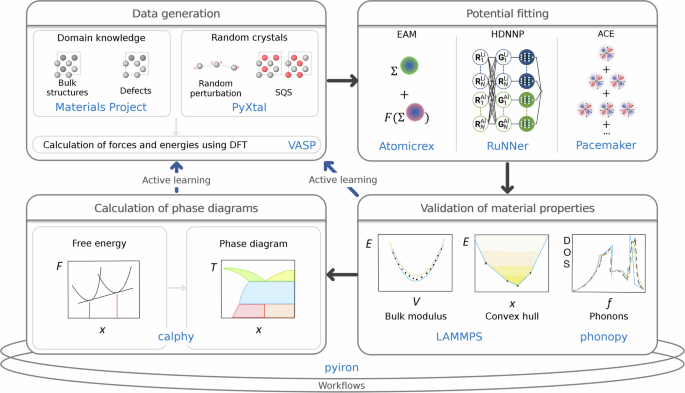
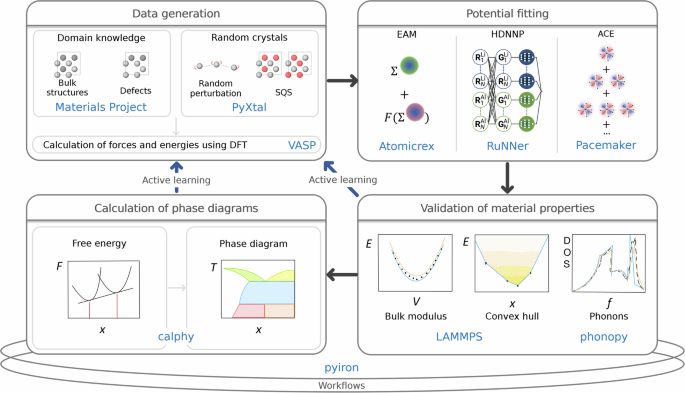
我们的目标是展示三种代表性模型势的整个 MLP 开发周期，以向感兴趣的研究人员阐明完整的过程，而不是对不同类型势的基准比较。我们引入了一套标准化工作流程，涵盖从 DFT 数据生成到 MLP 拟合和验证的所有方面，如图 1 所示。1。作为高级应用的示例，我们评估了原型二元系统的相图。这里介绍的工作流程是可重用的、可重复的，最重要的是，基本上是自动化的。在揭示所涉及方法的所有复杂性的同时，我们表明它们显着降低了技术复杂性。通过提供计算机代码和软件工具，我们鼓励将这份手稿用作现代 MLP 开发以及高级热力学应用领域的从业者指南。

这里，吡隆用作工作流程管理器来组合不同的软件工具和软件包。

作为模型案例，我们选择二元铝锂系统^24,25。铝锂合金具有低密度和高机械强度，非常适合航空航天应用^26,27。除了最近的作品²⁸，该系统缺乏原子间潜力，从 MLP 开发的角​​度来看，它既是理想的选择，也是具有挑战性的选择。我们选择了原子间势的三个典型例子：基于嵌入原子方法（EAM）的经典中心力势^29,30，高维神经网络势（HDNNP）^31,32，以及原子簇扩展（ACE）^6,33。我们使用卡尔菲³⁴用于计算相图，并采用吡隆¹¹作为一个工作流创建和管理环境，汇集了各种软件工具。我们的目标是实现原子间势的无缝创建和验证，同时朝着公平（可查找、可访问、可互操作和可重用）数据和软件原则迈出一步^35,36在MLP开发领域。

吡隆作为自动化工作流程的平台

我们雇用吡隆¹¹作为 MLP 开发和验证所有阶段的工作流程环境，如图 1 所示。1。开发周期有利于吡隆通过连接基本构建块：

1. 1.

   通用且易于使用的结构生成工具，结合了计算材料科学领域的标准软件库，例如日月光公司³⁷,皮马特根³⁸,皮克斯塔尔³⁹，以及其他方便且可互操作的包；

2. 2.

   各种电子结构和原子仿真软件包的可互操作接口，例如虚拟化服务提供商^40,41,42和兰姆普斯⁴³;

3. 3.

   能量、力和应力的通用存储格式，可有效用于在以下环境中实施的数十万种训练配置：吡隆作为班级训练容器（参见第“训练容器”部分）；

4. 4.

   这项工作中使用的拟合工具的通用接口，即起搏器^22,44,跑者^45,46,47， 和原子雷克斯⁴⁸，实施于吡隆作为潜在契合度班级;

5. 5.

   热力学特性验证工作流程和工具的通用接口，例如假声⁴⁹和卡尔菲³⁴。

块 (1) 使具有不同背景的用户能够轻松生成新配置或从现有数据库导入它们。块（2）中的通用接口提供了不同量子引擎或模拟协议之间的无缝切换，以在现有工作流程中进行最小的更改来创建训练数据。它还可以用于使用计算成本较低的较低级别方法来设计和测试工作流程，然后再切换到使用较高级别理论的生产运行。块 (3) 和 (4) 提供了在相同数据或选定子集上试验不同 MLP 形式的灵活性。此外，块（3）为块（2）中生成的所有类型的训练数据提供分析和绘图例程。最后，块 (5) 提供对验证例程的访问，帮助用户评估拟合 MLP 的质量。

Al-Li系统参考DFT数据集的构建

选择参数化原子间势所需的参考数据是 MLP 开发生命周期中最重要的步骤之一。为了创建参考 DFT 数据，我们采用了 VASP 5.4^40,41,42，使用第“VASP”部分中所述的工作流程。我们采用投影增强波（PAW）方法⁵⁰和 GGA-PBE 交换相关泛函⁵¹。进行了多次收敛测试，以确保获得的能量和力高度准确和一致。这些测试针对三种代表性结构进行，即面心立方 (fcc) Al、体心立方 (bcc) Li 和 B32 型β-LiAl，在其各自平衡体积附近的 30% 体积应变范围内。基于这些测试，使用了以下 DFT 设置：750 eV 的平面波截止、0.1 × k 网格间距…^Ø1，以及宽度为0.1 eV的费米涂抹法。通过这些设置，与在 800 eV 平面波截止和 0.05 eV 下执行的计算相比，我们观察到能量差异小于 0.5 meV/原子…^Ø1k 网格间距。

存在多种生成相关原子配置的策略。我们发现，领域知识、主动学习和随机搜索的结合可以有效地用于构建平衡的训练数据集。在这个三步策略中，首先利用领域知识根据标准晶体学数据库中可用的通用结构原型来选择结构⁵²。此后，我们在验证和模拟期间使用主动学习算法，并使用随机结构搜索过程获得随机配置⁵³来扩充数据集。

领域知识步骤侧重于已知对感兴趣的系统很重要的结构，并确保它们以高精度表示。在这项工作中，我们从材料项目数据库中查询了形成能小于或等于零的元素结构和二元结构⁵²。随后，对这些结构及其超晶胞应用了一系列变换，包括晶胞的均匀和非均匀变形以及原子的随机位移（参见补充说明）1-2）。这些步骤不仅确保了完美的整体结构，而且还确保了它们的变形，这对于再现弹性和振动特性至关重要，都包含在训练数据中。

然后，我们使用主动学习来确保即使在计算热力学属性所需的扩展模拟过程中（参见第“calphy”部分），电势也能保持稳定和准确。在主动学习循环中，我们根据高不确定性指标迭代选择结构⁵⁴来自对几个感兴趣的 Al-Li 相进行分子动力学模拟。

最后，我们添加了远离平衡的随机结构。此步骤确保配置空间的更广泛覆盖。仅依赖领域知识和主动学习可能会导致训练集目光短浅，从而妨碍拟合 MLP 的外推能力，而单独基于随机采样的方法可能会导致材料中缺失或代表性不足的重要相的风险。随机结构是根据最近的工作流程生成的⁵³利用 PyXtal³⁹软件如第“PyXtal”部分所述。我们为不同数量的原子生成了每个空间群的初始结构集（由于威科夫多重性约束，并非可以为细胞的每种组成生成所有空间群。），然后使用 DFT 对其进行松弛，首先只允许体积变化，然后是细胞形状和内部自由度的完全松弛。这些松弛不一定会导致势能景观中高精度的最小值，因此可以采用低精度 DFT 计算来加速这一步骤。然后使用所需的精度重新计算这些宽松的结构，以确保训练数据集的一致性。此过程与从头开始结构搜索方法非常相似⁵⁵，最初是为此目的而开发的，最近已应用于机器学习潜力⁵⁶。这种方法的主要优点是，它可以帮助在没有领域知识的情况下找到势能面的盆地，同时还将势能暴露于更多样化的结构和化学环境中⁵³。

最后，将细胞形状和尺寸的随机位移和变化应用于松弛结构，以获得势能表面最小值周围的附加样本。随机扰动的详细参数在补充说明中描述1。然后将初始随机晶体集以及最小化步骤和随机扰动产生的结构组合起来并添加到训练集中。完整的工作流程实施于吡隆以及前面 II A 节中介绍的原语。

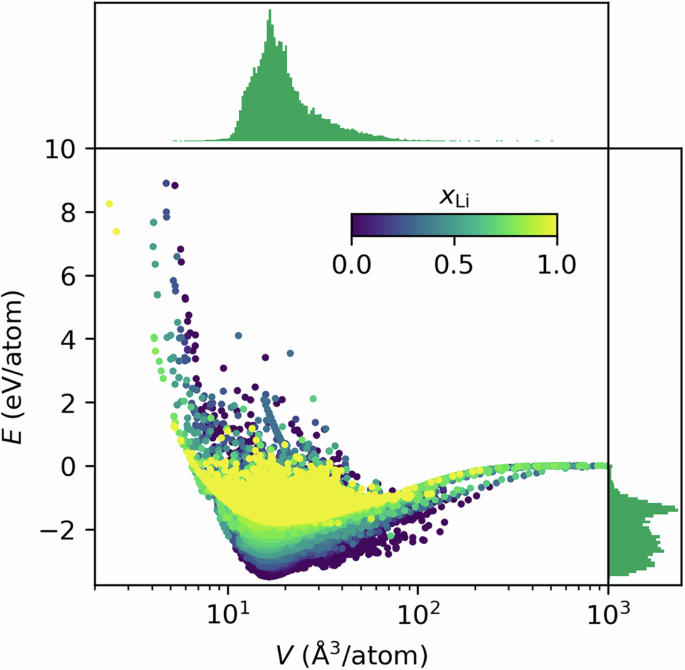
通过结合这三种策略（领域知识、主动学习和随机搜索），我们能够构建一个强大且广泛的原子结构数据集，捕获各种配置。DFT 参考数据在能量、体积和成分上的分布如图 2 所示。2补充图中提供了更多信息。1～3。

每个结构中锂原子的比例由点的颜色表示。

数据驱动的原子间势的训练

MLP 的训练通常使用针对特定模型架构定制的专用计算机代码进行。在我们的例子中，我们使用了原子雷克斯⁴⁸,跑者^45,46,47和起搏器⁴⁴分别拟合 EAM、HDNNP 和 ACE 参数化。由于拟合过程的差异，需要将训练数据集调整为各自的代码和模型。

对于 EAM 势，我们首先按照 Mishin 等人概述的方法拟合单个元素的势。⁵⁷。该方法通过相应地约束拟合参数来保证晶格常数、内聚能和体积模量的精确拟合。拟合描述 Al-Li 的函数参数，同时保持单元素参数恒定。训练数据仅限于整个集合的领域知识子组，包含 2081 个结构。由于势能的可调参数少于 100 个，因此训练数据量足够，并且可以加快参数化例程。此外，EAM 的函数形式灵活性有限，因此对远离平衡的随机采样结构进行训练可能会影响更重要的低能量结构的准确性。在拟合过程中，根据地层能量到凸包的距离对能量进行加权乙D_{（以 eV/原子为单位）为}$${W}_{E}=\frac{100}{{({E}_{D}+0.2)}^{4}},$$

有关拟合程序的更多详细信息，请参阅方法部分和参考文献。⁵⁷。有关所使用的函数形式和约束的详细信息可以在补充说明中找到3。

在开始 HDNNP 训练过程之前，通过消除与感兴趣的材料属性不相关的结构来细化训练数据集。这些包括在 12 × 半径内包含孤立原子而没有任何键合伙伴的结构、具有大正形成能或高排斥力分量的结构，以及原子体积在 10 × 区间之外的所有结构。…³/原子×50 ×…³/原子。总共删除了 4915 个数据点。

使用 RUNNERASE⁴⁷，然后我们进行网格搜索来优化 HDNNP 训练所需的超参数跑者代码^45,46。特别是，这包括原子中心对称函数 (ACSF) 的数量、短程截止半径和参数⁵⁸描述原子环境、优化算法的超参数（卡尔曼滤波器⁵⁹）和神经网络架构。对于每次试验，HDNNP 都接受了五个随机选择的小批量（每批 200 个数据点）和三个随机初始化种子的训练。1皮秒氮V时间在 300 K 和 1000 K 之间进行 MD 快速加热，以测试基本应用中每种潜力的能力。最后，根据该组 15 名成员的训练精度和模拟稳定性（稳定轨迹的长度、外推次数）选择最佳超参数。所选的超参数在补充说明中给出4和补充表3。然后，在整个训练数据集上使用选定的设置来训练 HDNNP，随机分为训练集 (90%) 和测试集 (10%)。所有数据点在训练过程中都被同等加权。这同样适用于总能量和分力的相对重量。

ACE 参数化是使用起搏器包裹⁴⁴。根据 DFT 相互作用的范围，所有相互作用的截止值设置为 7 ×。总数据集按 95% 比 5% 的比例随机分为训练集和测试集。训练结构的权重是根据其到凸包的能量距离分配的，遵循基于能量的加权方法⁴⁴。

我们使用越来越多的基函数（分层基扩展⁴⁴）并选择每个元素等于 1000 个函数的基组大小作为预测能力和计算性能之间的良好折衷。这一选择基于对能量、力、形成能和弹性常数的误差分析（更多详细信息请参阅 SI）。最终选择的潜在配置，即最大径向和角度指数，取决于相关阶数，以及其他 ACE 参数，请参见补充说明5。

最终的参数化是从头开始分两个阶段进行的。第一阶段更加强调力量（γ= 0.99），而在第二阶段，能量-力权重的分布更加平衡（γ= 0.3）被使用。在低于 2 × 的距离处添加了强的核心排斥对电势。

培训成果比较

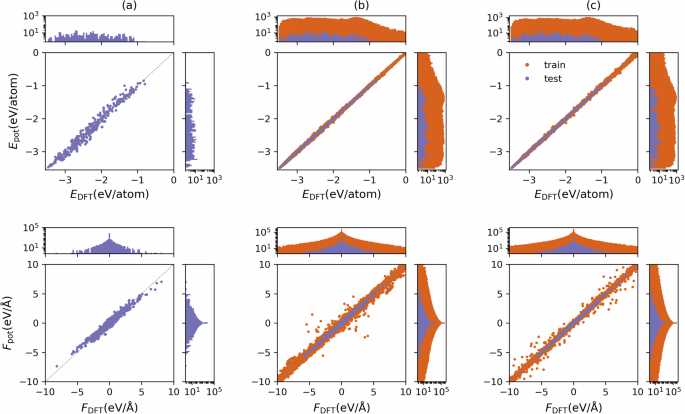
表中给出了所有训练数据集的概述以及所有三种潜力所达到的训练精度1图 2 提供了能量和力分量的预测值和参考值之间的相关性。3。

）而 HDNNP 和 ACE 电位显示在（乙） 和 （c）， 分别。表 1 中给出了 RMSE 和 MAE 的相应值。请注意，训练数据（紫色）是每个势的参考 DFT 数据集的不同子集，而测试数据（橙色）基于仅包含结构的公共测试集系统凸包上方 1 eV/原子以内。

可以看出，尽管训练集大小和组成不同，但所有三种拟合方法都产生了良好的训练结果。与我们的预期一致，受物理启发的 EAM 需要最少的训练数据，涵盖较大的能量、力量和体积范围，尽管代价是较高的训练误差。相比之下，HDNNP 和 ACE 利用了大部分可用的训练数据，并且相对于 DFT 参考值的误差比 EAM 更小。由于 ACE 势训练中采用的低能结构的权重较高，因此图 2 中接近于零的力周围的异常值较少。3c，而这样的权重尚未应用于HDNNP训练中。

为了促进验证并客观地比较所有潜力的准确性，我们创建了一个仅包含不属于任何训练数据集的结构的测试数据集。测试结构被限制在凸包上方 1 eV/原子或更小的范围内，因为它们代表了相图模拟的物理上最相关的子集。表中1和图。3，我们仅描述此常见测试数据集的测试集指标。对于所有潜力，测试误差指标都小于训练数据集的误差指标。就 ACE 而言，由于基于能量的权重分布不均匀，总体指标也存在偏差。

验证方法和策略

一旦电位参数化达到所需的精度，就必须对其进行广泛的验证。最终拟合的能量和力 RMSE 提供了相对于参考数据的潜力的首次定量评估。然而，必须评估更广泛的基本材料特性，并将其与 DFT 参考数据进行比较，并在适用时与实验观察结果进行比较。

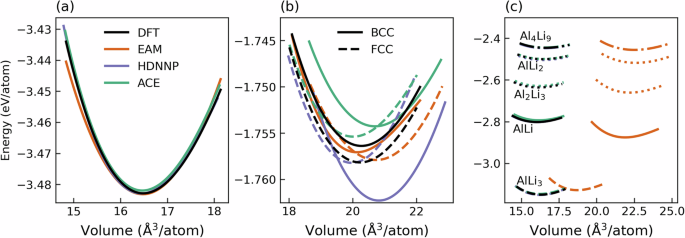
可转移性的基本评估是比较重要体相的能量作为原子体积的函数。该数据适合 Murnaghan 状态方程以获得 Murnaghan 曲线，该曲线不仅包含有关各相相互稳定性的有价值的信息，而且还可用于估计其体积模量。数字4显示了由 Al 的 fcc 相、Li 的 bcc 和 fcc 相以及五个二元相（AlLi、Al₃李艾尔₂李₃, 铝锂₂，和阿尔₄李₉）出现在相图中²⁵。

EAM、HDNNP 和 ACE 潜力的预测一个纯FCC铝，乙纯 bcc 和 fcc Li，以及c不同的AlLi化合物。DFT 参考以黑色显示。在 （乙），由于Li的体积模量（bcc为11 GPa，fcc为13 GPa）低于Al的相应值（76 GPa），因此能量范围较小，约为0.02 eV/atom，导致视觉效果相当大差异。对于 (c），HDNNP、ACE 和 DFT 的预测基本一致，因此很难区分。对于 Al 和 Li 的基态，所有电势都与 DFT 非常一致，但对于两个 Li 相，观察到了几 meV 量级的一些微小变化（请注意，根据参考 PBE-DFT 计算，基态为 fcc，尽管具有

与 bcc 相比，能量差异较小，如图 2 所示。4b).当考虑图 2 中的二元相时。4c，在 EAM 潜力和 MLP 之间观察到明显的区别。虽然 MLP 预测的原子体积以及形成能与 DFT 非常一致，但 EAM 势显示出对原子体积的相当大的高估。

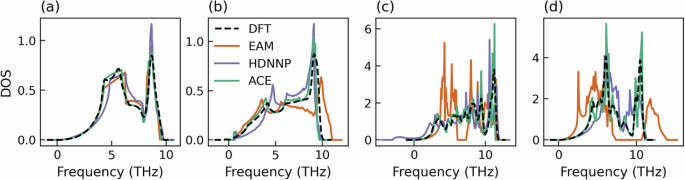
由势预测的声子与材料的振动特性相关，并反映了模型在平衡基态结构附近的小扰动的行为，这些扰动与相图的精确再现相关。数字5显示 fcc Al、bcc Li、AlLi 和 Al 的态声子密度₃李。请注意，我们将自己限制在两个二元阶段x_李–0.5，因为这是相图计算中考虑的区域（参见“热力学相图的构建”部分）。与 Murnaghan 曲线类似，我们观察到 HDNNP 和 ACE 都能以良好的精度预测声子 DOS，而 EAM 势则显示出二元相的显着偏差。

EAM、HDNNP 和 ACE 预测的态密度与 DFT 参考的比较一个FCC 铝，乙密件抄送李，c铝锂，和d铝3李。_{作为评估二元相图之前的第一步，我们评估并绘制了二元相的形成能作为 Li 含量的函数，如图 1 所示。}6。

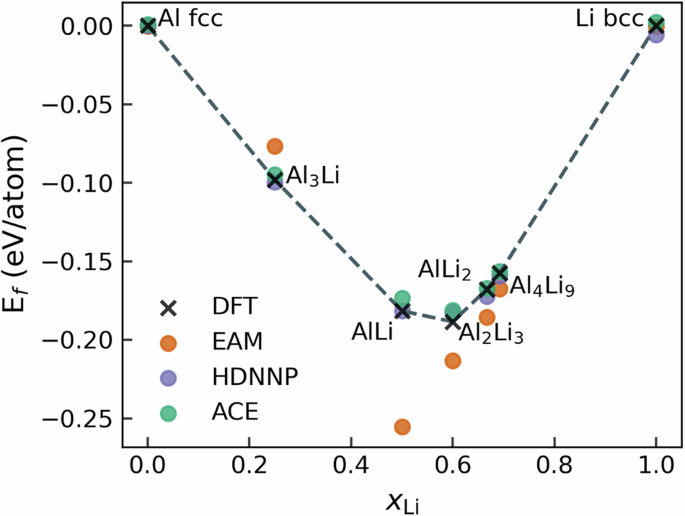
所谓的凸包实际上可以被认为是零开尔文的二元相图。凸包图允许将地层能量直接与 DFT 进行比较，我们的计算表明，HDNNP 和 ACE 都能以 DFT 精度很好地预测地层能量，而 EAM 预测则偏离参考值。图 6：EAM、HDNNP 和 ACE 预测的 Al-Li 二元系统的凸包。

弹性矩阵元素C

11_,C12_和C44_{对于 fcc Al 和 bcc Li 基态，使用拟合电位计算并在表中报告}2。对于 fcc Al，机器学习潜力与 DFT 参考数据非常匹配，而 EAM 潜力高估了 C₁₁并低估了其他两个弹性常数。对于 bcc Li，所有势都可以很好地描述弹性矩阵。

热力学相图的构建

相图提供了有关材料系统、预计在给定热力学条件下稳定的相以及一相转变为另一相或两相共存的条件的关键信息。因此，相图是原子间势的关键且具有挑战性的测试。一般来说，给定的原子间势应该能够重现相图的关键方面，或者至少是相图的一部分，与要使用原子间势的预期热力学区域有关。

卡尔法法⁶⁰可能是最著名的相图计算方法，并借助系统热力学性质的实验观察。从原子论的角度来看，存在不同的方法来确定相图^61,62。从广义上讲，这些方法可以通过共存相位模拟等方法直接评估相位稳定性^63,64,65，或间接地，通过确定相关相的吉布斯自由能或化学势⁶⁶。我们遵循计算自由能的方法，使用热力学积分方法，计算给定系统和参考系统之间的自由能差^67,68。我们将热力学积分与非平衡哈密顿插值和可逆缩放相结合，以有效地获得自由能（更多详细信息，请参阅方法）。这种计算的工作流程归结为第“calphy”部分中描述的代码。对于这种方法，需要有关相关阶段的先验信息，这是由当前建立的阶段图驱动的^25,69。为了拥有一套稳健、自动化和高效的相图确定工作流程，我们仅考虑非化学计量化合物中的替代缺陷，并将自己限制在相图的左侧，直到x_李= 0.5。因此，我们考虑类bcc B32晶格中的fcc Al、AlLi以及液体。此外，L12_—阿尔3_{Li在实验确定的相图中显示为亚稳态相}69^{，以及通过 DFT 计算确定的凸包（见图 2）。6}），这使得它成为相图计算中需要考虑的有趣候选者。对于纯铝，我们给出压力-温度磷

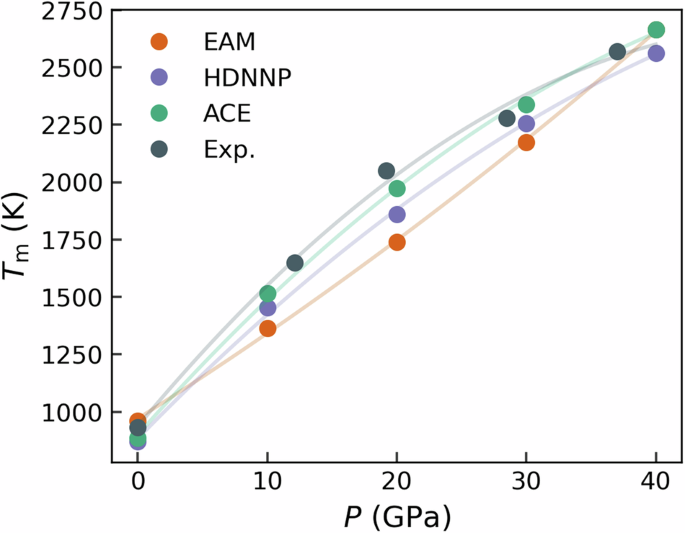
Ø时间相图。为了到达磷Ø时间在相图中，相关相的自由能根据温度和压力计算。为此，我们执行可逆缩放计算，提供给定温度范围内的自由能。选择 0–40 GPa 的压力范围，以 10 GPa 的间隔进行自由能计算。考虑面心立方和液相，并且在每个压力下，从自由能曲线的交点获得熔化温度。为两个相选择大约 7000 个原子的系统尺寸，以避免任何有限尺寸效应。对所有三个电位进行相同的计算，结果如图 2 所示。7。一般来说，所有三种势都紧密遵循实验的预测。虽然零压熔化温度与实验值相比被低估⁷⁰，它与从头计算的熔化温度相当⁷¹。

熔化温度，时间米，计算 EAM、HDNNP 和 ACE 在不同压力下的值。_{由激光熔化实验确定的熔化温度}94^{标记为灰色。}为了构建二进制相图，在组成范围0中考虑了FCC和液体。

x李_{0.5，b32 alli在0.4中}x李€0.5，Al₃li在0.2_x李€0.3。_{我们选择了Alli和Al的组成范围}3_{LI基于实验相图中的相关区域。}然后，我们确定这些相的自由能显着高于所选组成范围之外的其他阶段。为了创建具有LI的富含Al的FCC晶格，将Al原子随机选择并由LI取代，也就是说，我们假设Li杂质占据了替代晶格位置。同样，在B32结构中引入了替代性杂质，以产生化写计量学组合物。没有考虑其他机制，例如空缺或间质。

在选定的组成范围内，我们以所有相的组成间隔进行自由能计算。在每个组成下，考虑了600和1000 K的温度，并且使用可逆缩放方法在单个计算中获得该范围内的自由能。用25 ps的时间尺度进行自由能计算，用于平衡，50 ps进行切换，每个阶段的系统大小约为7000个原子。

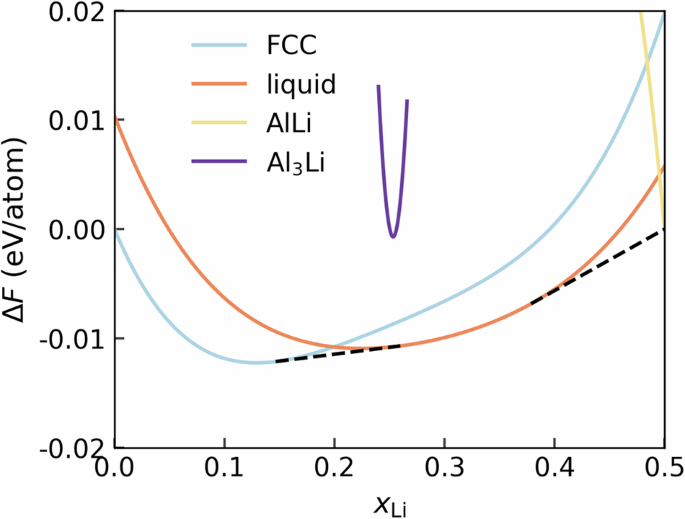
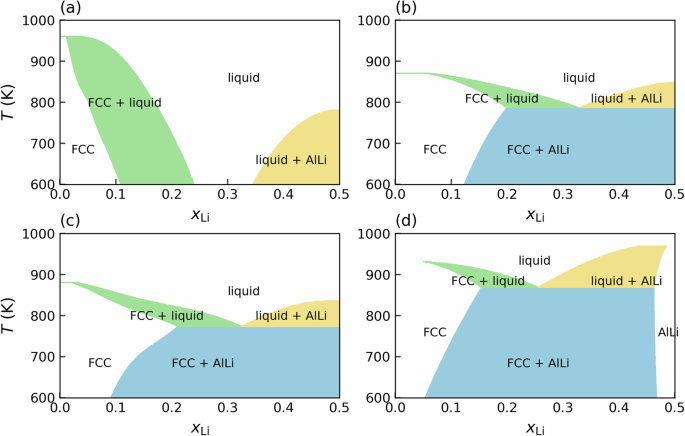
一旦获得了自由能，在每个温度下，将提取各个相的自由能，如图1所示。8。我们工作流程的当前局限性是，由于固相中的构型熵，它不包括对自由能的贡献，因此理想的混合贡献被添加到FCC，B32，远距离计量阶段。为了计算混合的自由能，选择最终成员为最低自由能的相位x李_{= 0 和}x李_{在给定温度下= 0.5。}最后，在每个温度下计算凸壳以提取每个阶段的稳定性区域。在这种结构之后，可以获得相稳定性和共存区域。再次，对所有三个电势进行了计算，结果如图2所示。9A c。参考阶段图是使用calphad方法计算的pycalphad⁷²工具，带有参考文献的Alli数据库。⁷³，如图所示。9d.

两相共存的区域是通过常见的切线构造来识别的，该构造由黑色虚线指示。

使用（使用的相图一个）EAM，（（乙）hdnnp，（（c）王牌。在 （d），显示了使用Calphad方法计算的相图。

HDNNP和ACE展示了相图（图。9b，c）与calphad和实验相图都显示出极好的一致性。相图的主要特征，例如Li在Al晶格中的溶解度，Eutectic Point（液体 - FCC + Alli），液态线的一般形状都得到很好的再现。共晶组成和LI溶解度都接近实验观察中的范围。表中显示了最终构件的熔化温度，共晶温度，共晶组成和Li在FCC Al晶格中的溶解度的比较。3。EAM电位的相图，如图2所示。9c，不重现相图的特征，表明经验原子间潜能的可能局限性。即使与实验相比，EAM电势可以最接近纯Al的熔化温度估计，但它可以错误地预测竞争阶段的稳定性。因此，本研究中EAM电位的适用性仅限于纯相的性质，例如弹性常数。

与图1相比，使用MLP计算出的相图显示出一些差异。9D和实验的相图。两种MLP都将AL的熔化温度和共晶温度的熔化温度分别降低了约6％和12％，这是预期的，并且与DFT的熔融温度预测一致（参考。^74,75和⁷⁶其中引用中）。从图中可以看出，在增加压力下，MLP对较低的熔化温度的预测也很明显。7。

另一个主要区别是AL在Alli有序阶段的溶解度。实验和calphad相图显示了溶解度，而HDNNP和ACE预测相反。这种差异可能是由于相图计算工作流的限制，而不是原子间电位。这里介绍的计算相图的工作流只考虑了非化学计量化合物的替代缺陷。但是，在B32 Alli中，实验研究表明，在LI浓度较低的情况下，Li原子表现出空缺介导的扩散机理⁷⁷。排除空缺支持替代缺陷可能会导致Ali阶段AL的溶解度较低。此外，将需要包含不同机制来研究相图的区域x李> 0.5。_{但是，我们的工作流程可以扩展到替代缺陷之外。}虽然是Al

3_{li相位存在于DFT凸面上，它在给定温度范围内的计算相图中没有出现，这与先前的研究一致}78^。但是，在较低的温度下，ACE电位预测了FCC和Al的共存区域₃李和al₃Li和Alli，消失在580 K左右（请参阅补充说明6和补充图。8）。

最后，相图工作流程仅限于实心阶段中构型熵的理想混合近似⁷⁸。

总体而言，为了获得这项工作中提出的相图，我们需要大约120个分子动力学模拟，每个分子动力学模拟约为150 ps，即使使用更昂贵的MLP，这种方法在计算上也是可行的。除了选择相关阶段和温度范围外，其余工作流程可以完全自动化，从而可以计算相图是原子质潜在发展生命周期中的常规任务。我们观察到，相位自由能的1 MEV差异可能会导致计算的过渡温度最多50 K差异（请参见补充说明7和补充图。9）；这反过来又结合了预测过渡温度的DFT的局限性，表明与实验相图相比，过渡温度的差异是可以预期的。然而，计算出的相图对预测热力学潜力可靠的热力学条件非常有益，并且对于观察到的相变行为的解释。

讨论

在我们提出的框架中，建立在毕生龙集成开发环境（IDE）建立了一个全面，健壮且用户友好的平台，用于开发经验和机器学习潜力。我们通过运行现代化潜能的开发周期中所必需的所有任务，成功地证明了其多功能性，涵盖了系统密度的功能理论数据库的创建，DFT数据与各种原子间潜力（EAM，HDNNP和ACE）以及ACE和ACE的拟合拟合，以及随后通过主要自动化方法进行验证。在AL-LI合金系统的二进制组合物 - 模型相图计算中，该框架的功率和性能被举例说明，展示了其适用于在由数千个单独的原子结构组成的大数据集上运行高度复杂的模拟协议以及技术上的技术性模拟协议的适用性以及技术上的技术结构以及技术上的技术性模拟协议。重要而复杂的材料系统。

此处介绍的框架的潜在应用是广泛的。它的用户友好性和适应性使其成为不同领域研究人员的易于访问和开放的工具，为MLP开发提供了简化的方法。未来的努力可能着重于扩大可以合并的潜在类别的范围，从而进一步提高了框架对需要复杂模拟协议的广泛材料科学挑战的灵活性和适用性。正在进行的发展将寻求优化和自动化MLP开发周期的其他方面，从而使研究人员能够解决所需的更先进的材料属性，例如计算缺陷相图，热电行为或超导性，从而为更有效和可再现的研究实践铺平了道路。

我们设想了我们提出的框架作为基础平台，邀请研究人员探索和研究机器学习潜力及其多样化应用所打开的机会。对开放性，可重复性和自动化的持续承诺将我们的框架定位为在材料科学中使用机器学习方法的快速扩展景观中的创新和发现的灵活且可扩展的基础。因此，我们鼓励社区积极参与提供的计算机代码和软件工具，这些工具是通过Github和Conda公开提供的。

材料科学的工作流程

最近几年显示了使用高性能计算簇的巨大变化：虽然历史上大型的单片代码允许在越来越多的内核上进行更高的规模，但随着机器学习的出现，新型的计算变得越来越多重要的是，需要组合大量运行各种代码的中小型工作以获得最终结果。一个突出的例子是本文描述的机器学习潜力的拟合和验证。获得高质量电位所需的DFT计算数量在数十万多达数十万个单独的DFT计算范围内。如此众多的工作数据管理不仅需要存储输入和输出数据，还需要其状态，即是否成功运行，是否融合或是否流产。如果工作失败，则需要重新提交他们，并且可能有必要纠正其输入。对于几个10,000个计算的工作尺寸，即使是小的失败率也使手动处理效率低下。对于这些类型的高级计算，自动化工作流系统几乎是强制性的。

在目前的工作中，我们使用了毕生龙¹¹作为一个工作流平台，包括所有必要的工具来创建高级机器学习潜力。毕生龙提供适合这些任务的功能：它提供了一种简单的方法来运行大量DFT计算（创建参考数据集），执行培训并分析广泛的原子间潜在计算集（用于验证）。毕生龙提供了几个功能，使运行如此复杂的工作流程有效且直观。它的通用输入和输出提供了一种简单的方法，可以用另一种DFT代码或潜在/ML方法替换一个DFT代码。例如，要替换DFT代码，主要更改将是更改作业类型。指定基集的通用输入，K点采样等保持不变，将通过毕生龙进入特定于代码的格式。Jupyter生态系统内的紧密集成提供了对所有工作流程组件和数据的交互式易于访问，并且高级工作管理工具的可用性为高档提供了有效的途径，并在现代超级计算机体系结构上运行所有计算。

DFT计算

密度功能理论（DFT）是一种量子机械建模方法，它已成为材料特性的初始计算的事实上的标准，尤其是对于较大的系统尺寸。此方法允许计算材料属性，而无需拟合或经验参数，提供了一个严格且基于第一原理的框架，以提供适合经验或机器学习潜力所需的大型数据集。在DFT中，关键近似在于交换 - 相关（XC）函数。这种近似使高维多体相互作用还原为纳入Kohn-Sham方程中的3D平均场电位。

对所有可用的XC功能的限制是，它们不能系统地改进，即实验的偏差是固有的。常见功能（例如本研究中使用的PBE-GGA功能，通常都表现出与实验结果良好的一致性。但是，重要的是要注意，偏差存在偏差，键长的错误通常约为1％，弹性常数的差异可能达到10％，并且以100 k为单位的熔化温度误差。^74,75

虽然交换相关函数代表了DFT中唯一不可控制的近似值，但存在其他参数可以用于系统地提高准确性，尽管计算成本增加了。其中，定义基集的完整性和K点采样的平面波能切断特别重要。必须实现有关这些参数选择的材料特性的收敛性，尤其是在使用DFT数据来训练原子间电位时。不足的收敛不仅会导致与融合结果的非系统偏差，而且由于平面波基集的离散性质和K点集，能在能量表面引入类似噪声的不连续性。对于潜在拟合的DFT数据集的生成，因此至关重要的是要仔细选择这些收敛参数，以确保与目标误差相比，不连续波动的幅度仍然很小。要用于开发MLP，这通常意味着能量收敛到约1 MeV/Atom，而力收敛到约0.1 eV/ã。

当仔细选择这些收敛参数时，已知DFT在相似结构之间平滑插值。这种特征使DFT特别适合应用平滑能量表面和衍生物（例如力和应力）（例如发展原子间电位）的应用。

嵌入原子法

在EAM电位中，系统的能量由一对电位给出V和非线性功能F，称为嵌入能量

这里， -_我由下式给出 -_我=_j -（r_我j），称为电子密度。它是通过在固体中查看每个原子作为杂质的动机而动机的，该杂质嵌入了宿主基质中，因此会受到其电子密度的影响，从而导致具有吸引力的化学相互作用。然后，V可以被视为排斥核心互动²⁹。在现代EAM潜力中V, -和F选择最佳地重现某些属性，并不一定遵循这种动机所产生的约束，例如V通常包括有吸引力的术语。当自由选择这些功能时，EAM形式主义等于有效的中等⁷⁹和芬尼斯 - 辛克莱尔⁸⁰潜力。我们紧密遵循的潜力遵循Mishin等人应用的程序。⁵⁷。

高维神经网络潜力

第二代HDNNP的发展的基础，Behler和Parrinello于2007年推出^31,32，是总能量乙_总计系统可以分解为中号依赖环境原子能贡献乙_我，使得

这种方法扩展了MLP对包含大量原子的凝结系统的适用性，是基于以下假设：对于许多系统，原子能对良好的近似是一种局部特性，仅取决于中央原子与其中央原子的相互作用半径范围内的相邻原子rc。_{该截止球内的环境由矢量捕获}\（\ oftrightarrow {{g} _ {i}} \）\）以原子为中心的对称函数，这又取决于所有邻居的坐标，同时保持强制性的旋转，翻译和置换不变。这些多体描述符的功能形式在其他地方更详细地描述⁵⁸。每个条目\（\ oftrightarrow {{g} _ {i}} \）\）被传递给特定于特定元素的馈电神经网络的输入节点，该节点提供原子能作为其输出。

在训练过程中，所有原子神经网络的权重都根据训练数据集中的总能量和原子力成分的损耗梯度进行迭代更新，以实现训练集中参考值的最佳匹配。有关HDNNP的构建和培训的更多信息，请参见参考。⁴⁵和参考。⁷。

原子簇扩展

原子簇扩展（ACE）³³介绍在原子环境空间中完成的基础函数。与HDNNP和其他MLP相比，能量由截止球体内的单个原子能总和表示氮原子，$$ {

-我），在ACE中被扩展为_{$$ {\ varphi} _ {i} = \ mathop {\ sum} \ limits_ {v}^{{n} _ {v}}} {c} {}$

cv_{是扩展系数}nv_基础功能乙我v_{。在线性王牌中，}乙我直接写为_{$$ {e} _ {i} = {\ varphi} _ {i} \，。$$}(6)

。，{\ varphi} _ {i}^{（p）}）\，$$

\（{\ Mathcal {f}} \）\）可以是任何一般的非线性函数。这项工作中使用的ACE电位采用了一种轻度的非线性形式，具有两个原子特性和正方形嵌入，如Finnis sinclair方法

热力学

通过原子模拟计算自由能的最广泛使用的技术之一是热力学整合^67,68。在这种计算技术中，感兴趣的系统和具有已知自由能的参考系统与参数耦合我”。联合系统的哈密顿量由

在哪里H_我，是具有已知自由能的初始或参考系统，并且H_f是最终系统，也是感兴趣的系统。如果感兴趣的系统处于固态，我们使用非相互作用的爱因斯坦晶体⁸¹作为参考状态，而对于液体，uhlenbeck-ford模型⁸²被雇用。两个系统之间的自由能差可以计算为

该集成必须通过离散的我”数组，因此在计算上非常昂贵，这需要进行方法论上的改进。在热力学整合的非平衡方法中⁸³，耦合参数我”是时间依赖性的，并且初始系统和最终系统之间的切换是在一个时间依赖的计算中以向前和反向进行的。在这样的切换过程中完成的工作被计算为

这与自由能差有关F在两个系统之间，

乙^d是开关过程中的能量耗散，可以作为前向切换和反向切换之间的差异获得。非平衡方法可用于在给定热力学条件下有效计算关注系统的自由能（磷,时间）。一次自由能F（磷,时间）在给定的范围内，自由能是温度的函数时间到时间_f可以使用可逆缩放方法在单个计算中获得⁸⁴。这些方法和相关算法已在参考文献中进行了详细讨论。³⁴。

毕生龙毕生龙

是用于原子模拟的工作流框架，侧重于快速原型和上刻度模拟协议。基于以对象为导向的方法，模拟协议的各个组件毕生龙像构建基块一样组合。每个毕生龙对象连接到基于jupyter的用户界面，结合结构化数据库（SQL）和层次结构文件格式（HDF5）的数据存储接口，以及用于连接计算资源和参数数据库的资源接口。通过实施潜在的拟合代码（Atomicrex,跑步者和起搏器），仿真代码（lammps和vasp）和热力学代码（卡尔菲）基于同一职位类别，执行基础代码的技术复杂性大大降低了。除了这里讨论的三个类别的原子量外，毕生龙也可以用于参数量张量电位⁸⁵，除了角度依赖电位⁸⁶和Tersoff⁸⁷经典的原子势。

作为模拟协议的第一步，新项目被初始化：pr = project（“ alli”）。项目对象表示为文件系统上的文件夹，并且该项目中的所有计算将在此文件夹中执行。从项目对象中，单个作业对象是使用分解模式创建的：

job = pr.create.job.simulationCode（'job_name'）

保理模式是指使用一个对象创建不同类型的对象，具有两个优点：一方面，它允许用户在选择创建新对象并另一方面使用自动完成对象。可以用它创建的对象的信息初始化。在这种情况下，工作对象从项目对象中接收其存储位置。个人的职位课vaspDFT代码，不同的拟合代码以及卡尔菲和lammps为了验证以下介绍。

Pyxtal

对于随机晶体结构的产生，我们包裹了Python代码Pyxtal在structuretoolkit模块与卵龙分发。

导入structuretoolkit.build.random作为stkr

al_li_structures = stkr.pyxtal（

组= [227，194],物种= [“ al”，“ li”],

num_ions = [4，4],重复= 10

）将生成用stoichoimetry al的每个太空组227和194的十个结构的列表

4

李

4_。作为文档的更高级选项_Pyxtal库本身也可以传递给该功能。vasp从维也纳的初始模拟包（VASP）开始

40

,^{41,42，使用保理模式从项目对象创建作业对象，并在原子}由原子模拟环境（ASE）定义的格式被分配：job = pr.create.job.vasp（“ job_name”）Job.tructure =结构

除原子结构外，还可以直接通过

毕生龙

Python接口。为了这毕生龙提供两个接口，首先是独立于特定仿真代码的通用接口，其次是特定于代码的接口，该接口允许已经使用特定仿真代码的用户直接修改特定的输入参数。使用通用界面，平面波能截止设置为750 eV，K点密度设置为0.1â…1^{并且电子收敛的水平定义为10}8^EV：job.set_encut（750.0）

job.set_kpoints（k_mesh_spacing = 0.1）

job.set_convergence_precision（

电子= 1.0E-8

,）

job.set_occupancy_smearing（

- 涂抹=“ fermidirac”

,宽度= 0.2,

）使用通用界面的优点是，用户可以通过更改创建作业函数调用可以在不同的DFT模拟代码之间切换

pr.create.job.vasp（）

，其余的命令保持不变。适用于专家用户毕生龙还提供了直接访问仿真代码特定输入的选项。例如，虽然可以使用通用元素指定电子涂抹set_occupancy_smearing（）功能，也可以根据vasp命名的特定输入文件英卡，可以在毕生龙像python词典一样：

job.input.incar [“ ismear”] = -1

job.input.incar [“ sigma”] = 0.1

最后，除了模拟代码特定参数外毕生龙作业对象还提供了指定提交高性能计算（HPC）排队系统的选项：

job.server.queue =“ gpu_queue”

job.server.cors = 4

job.server.gpus = 4

在完成输入参数和资源分配的规范之后毕生龙作业对象可以使用跑步（）功能。这触发了编写输入文件的内部周期，将计算提交到HPC进行执行，并且一旦计算完成，分析输出文件以将输出提供给Pyiron Python接口。

训练范围

在执行DFT计算之后，下一步是这些计算的输出的聚合，以将它们提供给原子间电位的拟合代码。在毕生龙这是通过组合两个对象来实现的毕生龙桌子对象和训练范围。这毕生龙桌子对象指定一系列在给定的作业对象应用于每个作业对象的函数毕生龙项目，按照地图减少模式：

表= pr.Create.table（）

table.add.get_job_name

table.add.get_structure

table.add.get_energy_tot

table.add.get_forces

table.run（）

然后将汇总的数据返回为PANDAS DataFrame对象，然后存储在训练范围在拟合代码中参考：

tr = pr.create.job.trainingcontainer（“ tc_job”）

tr.include_dataset（table.get_dataframe（））

此外，该类定义了使图形创建（例如图1和图1）的常见绘图。6和4例如，更容易

tr.plot.energy_volume（）

Atomicrex

这Atomicrex接口公开代码的完整功能⁴⁸在一个毕生龙Python接口，同时存储复制拟合过程所需的相关输入和输出。一个Atomicrex可以用

job = pr.create.job.atomicrex（“ atomicrexjob”）

现在Atomicrex实现EAM，修改的EAM³⁰，角依赖⁸⁸，分析键顺序⁸⁹和Tersoff⁸⁷潜力。他们可以使用

pot = job.factories.potentions.potential_type（）

对于允许使用不同功能形式（例如EAM电位）的电位，有必要定义这些功能。在这里，用户可以在预定义的功能和自己的创作之间进行选择。

莫尔斯= job.factories.functions.morse_b（

标识符=“ V”,

d0 = 0.05,

R0 = 2.5,

beta = 2.2,

s = 2.4,

delta = 0.0,

物种= [“ al”，“ li”]

）

uf = ref.factories.functions.user_function（

标识符=“ userElelement1Element2”,

Input_variable =“ r”

）

uf.expression =“ a*exp（r0-r）”

uf.derivative =“ -a*exp（r0-r）”

uf.parameters.add_parameter（“ A”，3）

uf.parameters.add_parameter（“ R0”，5）

pot.pair_interactions [Morse.Identifier] = Morse

pot.electron_densities [uf.Identifier] = uf

结构和相应的拟合属性可以使用常规直接分配训练范围界面。如果需要对重量的细粒度控制，也可以一一添加它们：

s = pr.create.structure.ase.bulk（“ al”）

job.structures.add_structure（s,

标识符=“ somerstructure”,

相对_Weight = 10000）

job.structures.add_scalar_fit_property（

“原子能”,

target_val = -4.0,

相对_ Weight = 100,

）

可以使用数学解析器表达式添加几乎任意参数约束：

job.input.parameter_constraint.add_constraint（

标识符=“ somecontstraint”,

依赖性=“约束参数”,

表达=“ MathParserexpression”,

）

最后，用户可以在内部LBFGS最小化器和通过NLOPT库提供的大量优化算法之间进行选择⁹⁰适合潜力。

algo = job.factories.algorithms.some_algo（

max_iter = 1000

）

job.input.fit_algorithm =算法

跑步者

与跑步者通常通过三个阶段：在模式1中，计算整个训练数据集的原子中心对称函数的值并将数据存储到磁盘上，并且将数据分开为训练和测试集。模式2优化了HDNNP的参数，以最好地表示参考能和力。最后，模式3用于预测未知配置的属性。

这毕生龙工作RunnerFit反映这些步骤。与其他培训工作类似，它是通过调用创造一个例程毕生龙项目目的。每一个RunnerFit作业还需要培训数据集的规范。

mode1 = proj.create.job.runnerfit（'mode1'）

MODE1.ADD_TRAINAN_DATA（数据集）

在下一步中，必须将一组以原子为中心的对称函数进行参数化。亚军提供程序generate_symmetryfunctions帮助完成此任务。之后，可以使用跑步命令：

sfs = generate_symmetryfunctions（数据集）,

sftype = 2,

截止= 12.0

）

Mode1.Parameters.SymFunction_Short += SFS

mode1.run（）

成功终止模式1之后，模式2是通过重新加载第一份作业并更改设置开始的。runner_mode。这告诉了基础跑步者代码如何操作：

mode2 = mode1.restart（'mode2'）

mode2.parameters.runner_mode = 2

mode2.run（）

遵循相同的过程来运行模式3。RunnerFit，模式3的执行是必须完成培训并获得火车和测试数据集的完整预测：

mode3 = mode2.restart（'mode3'）

Mode3.Parameters.runner_mode = 3

mode3.run（）

为了在应用程序中使用受过训练的潜力lammps，可以打电话给get_lammps_potential返回所需的例行程序PAIR_STYLE和PAIR_COEFF命令。HDNNP对样式是lammps界面由N2P2包裹⁹¹：

模式3.GEG_LAMMPS_POTENTION（）

起搏器

为了设置起搏器工作，需要创建相应的毕生龙工作并添加培训数据集。

job = pr.create.job.pacemakerjob（“ pacemaker_job”）

job.add_training_data（数据集）

ACE参数化过程的参数将初始化为其默认值。但是，人们总是可以配置所有这些。例如，设置能量权重平衡（κ来自参考。⁴⁴） 作为

job.input ['fit'] ['损失'] ['kappa'] = 0.3

之后，可以运行工作并获得lammps潜力也是如此。

卡尔菲

获得第三节F节所述的自由能的计算方法包括多个相互依存的步骤，并提出了一个复杂的计算工作流程。In order to facilitate a user to easily calculate the free energies, and at the same time retain the ability to tune each step in the workflow as needed, we developedcalphy³⁴, a python library for automated calculation of free energies.它使用LAMMPSas the molecular dynamics driver to perform free energy calculations in an automated manner.calphywhen combined withpyiron, can leverage additional features such as interoperability with other common atomistic simulation tools, scaling to HPC systems, and job and data management.

之内pyiron, a non-equilibrium free calculation, for example an Al fcc lattice at 500 K and 0 pressure can be carried out by the following code:

pr = Project("free_energy")

job = pr.create.job.Calphy("Al_fcc_500")

job.structure = pr.create.structure.ase.bulk("Al",

 cubic=True).repeat(4)

job.potential = "Al-atomicrex"

job.calc_free_energy(

 temperature=500,

 pressure=0,

 reference_phase="solid",

 n_equilibration_steps=25000,

 n_switching_steps=50000,

）

job.run()

The main inputs needed are the input structure and the interatomic potential, apart from the thermodynamic conditions at which the calculation is to be performed. For calculating the free energy of a liquid system, the only change needed isreference_phase='liquid'。calphyautomatically uses a different reference system based on this command. To obtain free energies over a given temperature range, one needs to change the temperature option:temperature=[500, 800]。In this case, a free energy calculation at 500 K is performed first, followed by a temperature integration up to 800 K in another calculation.

LAMMPS

Beyond the free energies calculated withcalphyto construct the phase diagram, theLAMMPSmolecular dynamics simulation code is used to validate material properties calculated with the individual machine learning potentials. In pyiron the workflows to calculate the material properties is defined independent of the specific simulation code, so in the first step a referenceLAMMPSjob is defined for the interatomic potential fitted with theatomicrexfitting code:

pr = Project('validation')

job = pr.create.job.Lammps('lmp')

job.structure = structure

job_lmp.potential = 'Al-atomicrex'

Following the definition of the reference job the next step is assigning this reference job to the workflow to calculate a material property, in this case the calculation of the elastic constants with theElasticMatrix工作：

elastic = pr.create.job.ElasticMatrix('elmat')

elastic.ref_job = job_lmp

elastic.run()

By defining the calculation of the material properties independent of the simulation code, the same validation calculation can be applied for theLAMMPSmolecular dynamics simulation code to test the fitted interatomic potentials as well as theVASPDFT simulation code, to enable a direct comparison.

作者和单位

1. Max-Planck-Institut für Nachhaltige Materialien GmbH, 40237, Düsseldorf, Germany

   Sarath Menon

2. ICAMS, Ruhr-Universität Bochum, 44801, Bochum, Germany

   Yury Lysogorskiy, Minaam Qamar, Matous Mrovec & Ralf Drautz

3. Lehrstuhl für Theoretische Chemie II, Ruhr-Universität Bochum, 44780, Bochum, Germany

   Alexander L. M. Knoll & Jörg Behler

4. Research Center Chemical Sciences and Sustainability, Research Alliance Ruhr, 44780, Bochum, Germany

   Alexander L. M. Knoll & Jörg Behler

5. Technische Universität Darmstadt, Fachbereich Material und Geowissenschaften, Fachgebiet Materialmodellierung, 64287, Darmstadt, Germany

   Niklas Leimeroth, Jochen Rohrer & Karsten Albe

6. Max-Planck-Institut für Eisenforschung GmbH, 40237, Düsseldorf, Germany

   Marvin Poul, Jan Janssen & Jörg Neugebauer

贡献

Conceptualization: K.A., J.B., R.D., J.N. Data curation, Formal analysis, and Investigation: S.M., Y.L., A.K., N.L., M.P., M.Q. Methodology: S.M., Y.L., M.P., J.B., R.D., J.N. Software: S.M., Y.L., A.K., N.L., M.P., M.Q., J.J. Validation: S.M., Y.L., A.K., N.L., M.P., M.Q. Visualization: S.M., Y.L., A.K., M.P. Writing - original draft: S.M., Y.L., A.K., N.L., M.P., M.Q., J.J., M.M., R.D., J.N. Writing - review & editing: S.M., Y.L., A.K., N.L., M.P., M.Q., J.J., M.M., J.R., K.A., J.B., R.D., J.N. These author contributions are defined according to the CRediT contributor roles taxonomy.

通讯作者

通讯至Sarath Menon或者Jörg Neugebauer。

利益竞争

J.N.is an associate editor for npj Computational Materials.其他作者声明没有竞争利益。

开放获取This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a链接到知识共享许可证，并指出是否进行了更改。本文中的图像或其他第三方材料包含在文章的知识共享许可中，除非材料的出处中另有说明。如果文章的知识共享许可中未包含材料，并且您的预期用途不受法律法规允许或超出了允许的用途，则您需要直接获得版权所有者的许可。要查看此许可证的副本，请访问http://creativecommons.org/licenses/by/4.0/。转载和许可

关于本文