生成学习辅助随机退役条件下可持续电池回收的健康状况估计

交通电气化是低碳能源转型的关键领域¹，前所未有地重塑了基于化石燃料的运输范式。锂离子电池为电动汽车 (EV) 提供经济实惠、耐用且安全的能源供应，对于这一转变至关重要^2,3。到 2050 年，使用中和报废电动汽车电池的总容量将超过 32×62 太瓦，远高于国际可再生​​能源机构和存储实验室情景中的估计⁴。然而，退役的电动汽车电池受到严格监管，剩余容量巨大，未得到充分利用，通常超过额定容量的80%^5,6。如果处理不当，会造成经济负担⁷对于制造商和用户，以及随后的环境和社会问题⁸，包括资源浪费、供应链风险和碳排放^9,10,11。

解决电池报废间歇性激增问题的有前途的策略是重复利用^6,12,13和回收¹⁴。在再利用中，退役电池被重新用于并网储能系统等应用¹⁵, 住宅电源¹⁶和低速车辆。然而，重复使用需要初步预处理，包括一致性筛选^{17 号}、容量排序¹⁸，并重新组合^19,20以满足应用要求²¹。尽管启动了试点计划^22,23,24缺乏严格的使用场景和退役路径标准，阻碍了剩余产能的合理利用²⁵。回收利用退役电池的剩余价值，通过材料提取或结构修复^{26,27 号}，适用于不可逆退化的退役电池。与火法冶金和湿法冶金相比^28,29，直接回收因卓越的盈利能力、较低的能源消耗和减少的碳排放而脱颖而出^{26,27 号,30}。利用正极材料的补锂和后处理，直接回收实现材料结构的高效修复和性能恢复³¹。然而，健康状况（SOH）决定了直接回收策略配方中所需的化学试剂和预期的锂补充剂量^32,33,34。用量不足会导致修复不完全，用量过多会导致阴极表面产生残碱，降低修复性能^{27 号,35}。不幸的是，SOH 检索需要侵入性材料表征^36,37和漫长的容量校准测试，非侵入、快速和可持续的 SOH 采集仍然是一个突出的挑战。

为了确保一致的 SOH 信息，云平台对电动汽车电池进行监控并记录运行数据³⁸和电池护照²⁴。欧洲议会于 2023 年 6 月 14 日通过了《电池指令》，以确保退役电池在使用寿命结束时可以重复使用、翻新或回收³⁹。然而，所需的监控和记录程序只能在电动汽车服务阶段进行，退役电池不再连接到车载监控单元。因此，检索现场可用的 SOH 数据具有挑战性。生命周期数据完整性仍然是一个重大挑战，要求仅使用现场数据进行 SOH 估算，与历史数据相反或在可控条件下进行^30,40,41。一种解决方案是在退役电池收集场进行容量校准测试，即充电状态（SOC）调节，这很简单，但需要难以承受的测试时间和额外的电费。混合脉冲功率表征测试是通过动态脉冲注入估算 SOH 的替代方法，但完整的测试序列需要超过 12 小时。陶等人。利用短脉冲对退役电池进行 SOH 估计，假设执行 SOC 调节至 5% SOC，这与随机退役 SOC 条件几乎不兼容⁴¹。基于感官的测量的最新进展包括 X 射线成像⁴²，电化学阻抗^43,44, 光纤传感^45,46, 声学传感^47,48, 部分充电^49,50，和脉冲注入^{17 号,41}。由于入侵，基于传感的技术仍处于实验室阶段，而脉冲注入功能可以在不造成物理损坏的情况下解决电池退化问题，同时比部分充电和基于电化学阻抗的方法更快^{17 号,51,52,53,54,55}。然而，脉冲注入是一种以数据为中心的方法，只有在理想的假设下才可行，即物理测量的数据包含模型部署阶段的退役条件，这被称为机器学习社区中域转移的常见挑战。尽管迁移学习和领域适应方法取得了进步^56,57,58，挑战仍然存在，因为要对齐的目标领域仍然需要部署时的先验信息，并且现有的学习方法很难针对随机退休条件进行更新⁵⁹。另一种选择是在未探索的退休条件下扩大数据测试规模，以减轻数据稀缺性和异质性，同时可能导致成本增加。王等人。提出了一种温度挖掘方法来插值热化学过程中不同中间状态的反应动力学偏好，允许以最小的热化学实验规模和成本构建广泛的训练数据库，作为机器学习模型训练的数据增强⁶⁰。此外，生成学习还展示了使用部分循环配置文件中的增强数据估计 SOH 的可能性，保存所需的物理测试数据^61,62。然而，由于正极材料类型、物理格式、容量设计和历史用途的混合，电池再利用和回收环境中的数据稀缺性和异质性甚至更加复杂，限制了特定条件的降解知识与机器学习的潜在整合模型。因此，在数据生成时考虑退役条件和脉冲电压响应之间的依赖关系是合理的，无需同时进行冗长的时间序列容量校准和额外的物理实验，以提高SOH估计性能。

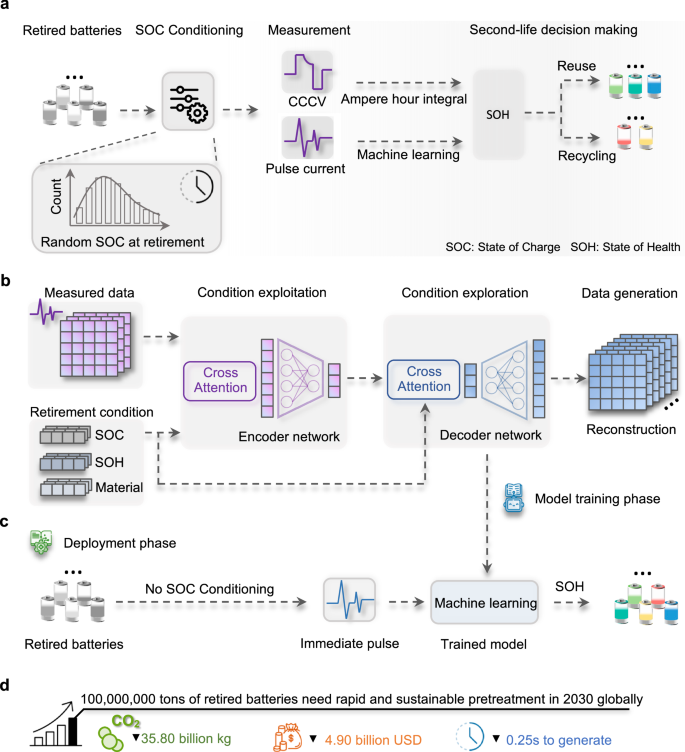
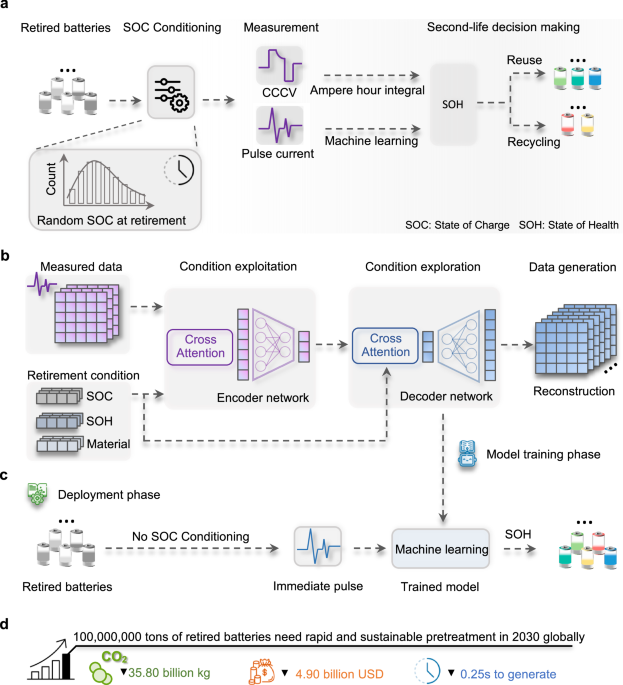
在本研究中，我们使用注意力变分自动编码器生成的脉冲电压响应数据来执行退役电池预处理，即 SOH 估计，从而节省了物理测量时间和成本。一般预处理步骤、生成模型训练和实际模型部署步骤的高级流程如图 1 所示。 1。研究思路是利用生成学习来利用已测量的数据来探索连续退役条件下的脉冲电压响应，即退役电池收集阶段的 SOC 分布。下游 SOH 估算的实施无需物理测量的脉冲响应数据，从而节省了预处理电力成本和碳排放量，否则需要将 SOC 调节至预期水平。与安时积分法和机器学习脉冲注入相比，生成学习强调更快的生成速度和准确的估计。利用生成的数据，简单的回归器可以在数据库中看不见或无法访问的 SOC 报废条件（这是一个具有挑战性的分布外 (OOD) 问题）下以较低的误差成功估计 SOH。通过学习 SOC 条件和快速脉冲引起的电压响应之间继承的物理模式，可以解决 OOD 问题。我们通过 2700 个物理测量样本进行验证，涵盖 3 种正极材料类型、3 种物理格式、4 种容量设计和 4 种历史用途（1 个实验室加速老化、1 个纯电池电动汽车驱动和 2 个混合电动汽车驱动），展示了我们方法的普遍性）。生成学习通过将退休条件的先验知识集成到模型参数的潜在空间缩放中，适合插值和外推，节省测量时间、电力成本和随之而来的碳排放，同时不影响 SOH 估计的准确性。一项关于 2030 年电池退役的保守全球案例研究强调了快速、可持续的 SOH 估算在火法冶金、湿法冶金和直接回收环境中的重要性。通过技术经济分析，生成学习辅助的 SOH 估算可以节省 49 亿美元的电力成本和 358 亿公斤的二氧化碳2_{到 2030 年全球排放量。}我们讨论了模型的可解释性、回收预处理的影响以及与机器学习相结合的未来智能回收预处理方向的更广泛的方面。

退役电池预处理步骤包括 SOC 调节、物理测量、用于 SOH 诊断的机器学习以及再利用或回收之前的二次生命决策过程。SOC调节是指使用传统的恒流恒压（CCCV）方法将退役电池的SOC值调整至所需水平。乙用于生成脉冲电压响应数据的注意力变分自动编码器的示意图。c用于 SOH 估计的数据生成模型的实际使用不需要额外的 SOC 调节。经过训练的机器学习模型由生成的数据进行监督，并在部署阶段接收即时脉冲电压响应。d我们的生成学习方法通​​过在 2030 年全球电池退役场景中节省 SOC 调节成本，带来经济和环境效益以及快速生成速度。结果

数据稀缺和异构性是数据驱动的电池诊断和预测的主要挑战，特别是对于退役电池。

我们从 270 个实际退役的电池中收集了 2700 个样本，涵盖广泛的 SOC 水平，即从 5% 到 50%，颗粒度为 5%。如图所示 2a，该数据集涵盖 3 种流行的正极材料类型，包括 119 种物理收集的 NMC（镍锰钴氧化物）、56 种 LFP（磷酸铁锂）和 95 种 LMO（锰酸锂）退役电池，涵盖 3 种物理格式（圆柱形、袋装、棱柱形）和 4 种历史使用模式（1 种实验室加速测试、3 种电动汽车使用情况，其中包括 1 种纯电动动力总成模式和 2 种混合动力传动系统模式）。我们强调，包含高度异构的测试样本使我们的数据集成为迄今为止最大的基于快速脉冲的数据集，用于估计退役电池的 SOH，从而促进模型的通用性超越物理测量的数据集。

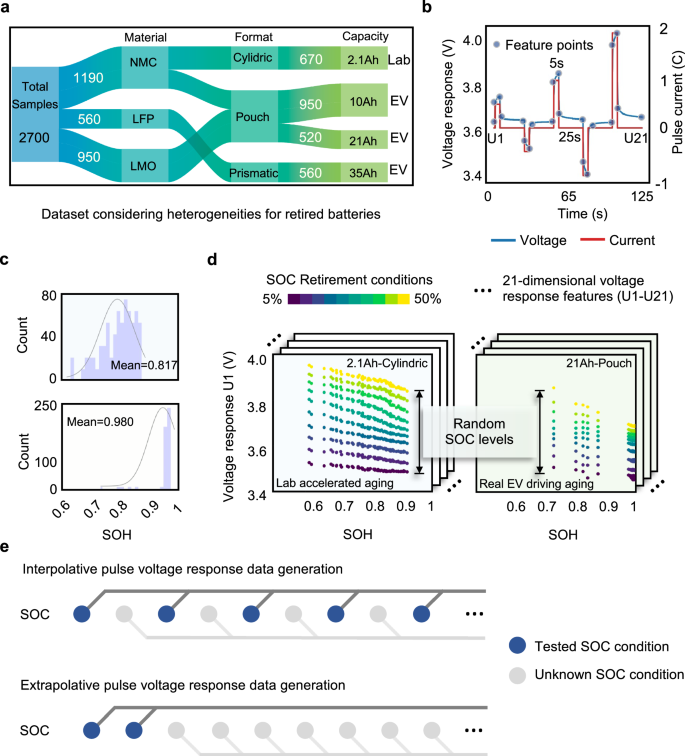
退役电池分布的桑基图包括正极材料类型、物理格式、容量设计和历史用途。乙退役电池的脉冲电流和随后的电压响应，其中特征是从转折点提取的，即电压响应曲线的二阶导数为零的点。提取从U1到U21的21个特征点。原始数据的记录频率为100Hz。C 速率中每个脉冲之间的休息时间为 25 秒。注意，术语C代表进行1小时的充电（放电）时的充电（放电）率。环境温度控制在25℃\(^{\circ}{{{\rm{C}}}}\)。c分别以 2.1 Ah 和 21 Ah 退役电池的健康状态 (SOH) 分布（高斯拟合）进行说明。对于其他电池类型的SOH分布，可以参考补充图1。 1。d在不同的充电状态 (SOC) 条件下，测得的脉冲电压响应与容量校准测试中校准的 SOH 之间的关系。图示了第一个特征尺寸 U1。e不同电池报废 SOC 分布下的插值和外推数据生成案例说明。详细的测试设置位于补充说明1和2，注意到各种阴极材料类型的 C 速率设置是相同的。源数据作为源数据文件提供。

与常规恒流恒压（CCCV）测试相比，脉冲测试不会造成冗长的测试时间和对报废电池的额外损坏。因此，我们使用 CCCV 结果作为 SOH 基准容量值。脉冲测试数据用作生成学习模型的训练数据。尽管电池正极材料类型各不相同，但我们执行标准化且易于访问的特征工程，确保实际使用中的兼容性。数字2b演示了脉冲电流注入后的特征提取。CCCV 和脉冲注入实验设置可以在补充说明中找到1。对于前五个注入脉冲，转折点（即电压响应二阶导数为零的点）被记录为特征，从而产生 21 维特征。尽管脉冲时间为 5 秒级别，我们还对脉冲宽度进行灵敏度测量，其双重目的是验证脉冲鲁棒性并进一步缩短测试时间（范围从 30 毫秒到 5 秒）。

我们在实验室测试中考虑加速老化（补充说明2）和真实的电动汽车驾驶老化，尽管由于数据隐私限制而无法了解明确的驾驶配置文件。如图所示 2c，示出了加速老化电池（NMC，2.1-Ah）和纯电动汽车驱动老化电池（NMC，21-Ah）的SOH分布。注意到 SOH 值在较宽的 SOH 区域（从 0.6 到 1）中是互补的，收集的数据代表电池报废场景，也包括极端提前报废的情况。其他收集的电池（LMO、10-Ah 和 LFP 35-Ah）的 SOH 分布涵盖了广泛的 SOH 分布，请参见补充图。 1。脉冲测试在不同的 SOC 水平（范围从 5% 到 50%）下重复进行，以模拟退役电池收集的随机性。测试的 SOC 区域是假设退役电池要么表现出低 SOC，要么出于安全固定仓库存储要求而进行强制放电，因此 SOC 上限设置为 50%。如图所示 2d，示出了从加速老化电池（NMC，2.1-Ah）和电动汽车驱动老化电池（NMC，21-Ah）提取的特征的第一维。尽管容量设计和历史使用情况存在差异，但脉冲电压响应表现出一致的退化模式，其他退役电池的其他特征尺寸也是如此，请参见补充图。 2—5。然而，退役电池的SOC分布是连续的，因此无法通过物理测量来穷尽。我们不是跨越数据测试规模，而是使用已经测试的脉冲电压响应数据来生成跨 SOC 条件的更多样化的数据。如图所示 2e，说明了两代情景，即插值和外推，其中包括机组调节节省、节电、CO₂减排量及其计算方法见补充表。 1—3， 分别。

脉冲电压响应数据生成

我们首先考虑使用已经测量的脉冲电压响应数据来重建自身，而不是直接生成新的数据样本。重建意味着测量数据首先被压缩到潜在变量空间中，同时保持原始统计分布的学习结构（补充图1） 6）然后解压缩到原始尺寸。在本研究中，重构相当于监督编码器神经网络模型和解码器神经网络模型训练阶段，如图1所示。 1b。核心思想是利用退役条件和脉冲电压响应数据之间的潜在依赖关系以及交叉注意机制来平衡有限测量数据的利用和扩展数据空间的探索，请参阅“方法”。然后与条件信息融合的测量数据被输入编码器神经网络，获得包含退休条件的潜在变量。通过训练解码器神经网络模型并重建输入数据样本来解压缩压缩的潜在变量，同时也受到前馈退休条件的指导。解码器神经网络的另一个输入只是随机噪声，服从高斯假设（补充图1） 7），不造成任何物理实验测量，否则会涉及额外的测试时间、能源消耗，甚至安全隐患。

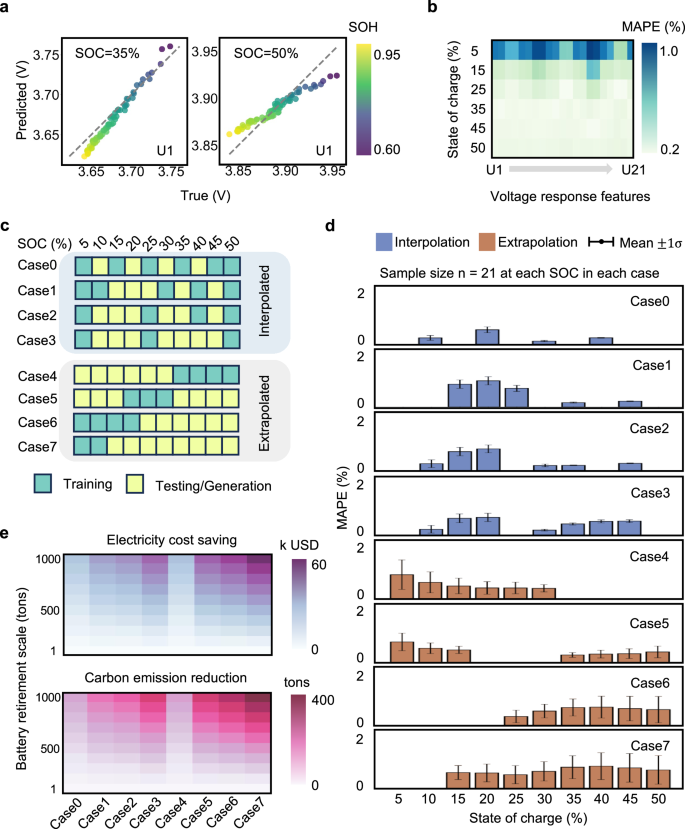
数字3a显示了在选定的 SOC 值（35% 和 50%）下第一特征维度 U1 的数据重建结果，平均绝对百分比误差（MAPE）低于 1%，表明模型学习了脉冲电压响应数据和SOC 条件。这种相关性在较宽的 SOH 范围内（从 0.6 到 0.95）具有普遍性。对于其他特征维度，数据重建结果仍然令人满意，MAPE低于1%，见图1。 3b。其他类型退役电池（NMC，21-Ah，LMO，10-Ah 和 LFP，35-Ah）的重建结果显示在补充图中。 8—10，展示了模型的通用性和灵活性。值得注意的是，较低 SOC 区域表现出相对较高的重建 MAPE，但仍低于 1%，这可以通过低 SOC 区域极化响应的敏感性来合理化。因此，建议在中间 SOC 区域执行脉冲注入，以可靠地表示电池退化情况。然而，当我们强调不同 SOC 的随机退休条件时，固定 SOC 的脉冲注入需要大量的调节时间和能量消耗，加剧了脉冲注入区域与难以承受的调节时间和成本之间的困境，请参见补充图 1。 11。

图中显示了模型训练结果（重建）的奇偶校验图，其中特征 U1 在选定的充电状态 (SOC) 条件（35% 和 50%）下。乙特征 U1 到 U21 的模型训练性能热图。c随机退役场景下退役电池的 SOC 仿真，包括插值和外推情况。d随机退休场景下的数据生成性能，其中误差线表示标准差（\({{{\rm{\西格玛}}}}\)）跨 21 维特征计算（n在每种情况下每个 SOC 处 = = 21），条形的高度表示其平均值。e节省电费和二氧化碳2_{使用不同数据生成案例设置的不同电池报废规模的减排量。}请注意，电池报废规模是对数的。所有结果均来自 NMC、2.1 安时电池以供说明。源数据作为源数据文件提供。

通过提出的生成学习方法，我们强调用于训练目的的已测量数据是以额外的物理测试为代价的，但是，生成没有额外的成本。如图所示 3c，我们验证了八种数据生成情况，包括插值和外推。在插值情况下（从 Case0 到 Case3），训练数据的 SOC 下限和上限分别固定为 5% 和 50%。相比之下，外推案例（从案例 4 到案例 7）意味着已测量的数据与未见过的 OOD 数据是互斥的，这在机器学习社区中是一个具有挑战性和开放性的问题。在这里，我们使用退役电池的先验知识来缩放编码器神经网络中的潜在分布，将已经测量的数据推广到 OOD 条件，请参阅方法。我们注意到 Case4 和 Case5 是玩具示例，因为这些案例的训练成本高于在未见的 SOC 条件下生成相同量的数据所节省的成本。然而，我们仍然使用玩具盒来证明潜在空间缩放在更广义的电池报废设置中的稳健性。因此，在实际使用中，用户可以根据模型训练成本和数据生成精度之间的权衡来定制数据生成策略。

如图所示 3d，说明了在不可见的退休条件下基于距离的数据生成性能。值得注意的是，训练后的生成学习模型用于生成更多数据样本，特别是在但不限于未见过的退休条件下。例如，案例3使用5%、25%和50% SOC下物理测试的脉冲电压响应数据来生成10、15、20、30、35、40和45% SOC下的数据。所有插值案例均表现出低于 2% 的低 MAPE 误差，即使模型从未使用此类数据进行训练。从直觉上看，外推 Case6 和 Case7 在节省预处理成本方面更有希望，因为所使用的训练数据检索起来既省时又经济。我们证明，即使在 OOD 情况下，生成学习策略也能成功引导已测量的数据泛化为 OOD 数据。如果没有潜在空间缩放，当物理测量的训练数据远离生成条件时，数据生成会表现出明显增加的误差，请参见补充图。 12。这种现象具有一个有吸引力的含义，即人们可以利用测量的数据来探索看不见的数据，以使用定制的生成策略检索更高成本的数据。关于基于分布的数据生成性能，该模型在验证设置中实现了较低的 Kullback-Leibler 散度，这表明该模型可以自动学习已测量数据的分布以创建多样化的数据实例，请参见补充图。 13—16。

我们评估电力和二氧化碳₂使用不同的数据生成案例节省排放。数字3e显示电量和 CO₂排放量节省量按升序排列，颜色条映射相应的值。除了 Case4 和 Case5 这两个玩具示例之外，外推策略最多可以节省 60,000 美元的电力成本和 460,000 公斤的二氧化碳₂排放量，假设电池报废规模为1000吨。这一优先级是通过从具有成本效益的物理测量数据生成昂贵的数据来实现的，这需要 SOC 调节成本。在插值生成过程中，我们发现该模型不需要严格的中间点进行插值，从而导致案例 3 中的使用优先级，使用 5%、25% 和 50% SOC 数据。尽管存在不同的情况困难，但数据生成模型很容易训练，在毫秒级内不到 50 次迭代即可收敛，请参见补充图。 17 号。一旦生成模型经过适当的训练，用户就可以在广泛的报废条件下生成无限的数据，而无需任何测量成本，从而促进快速、准确和可持续的报废电池 SOH 估计，以进行再利用和回收决策。

利用生成的脉冲电压响应功能估算报废电池 SOH

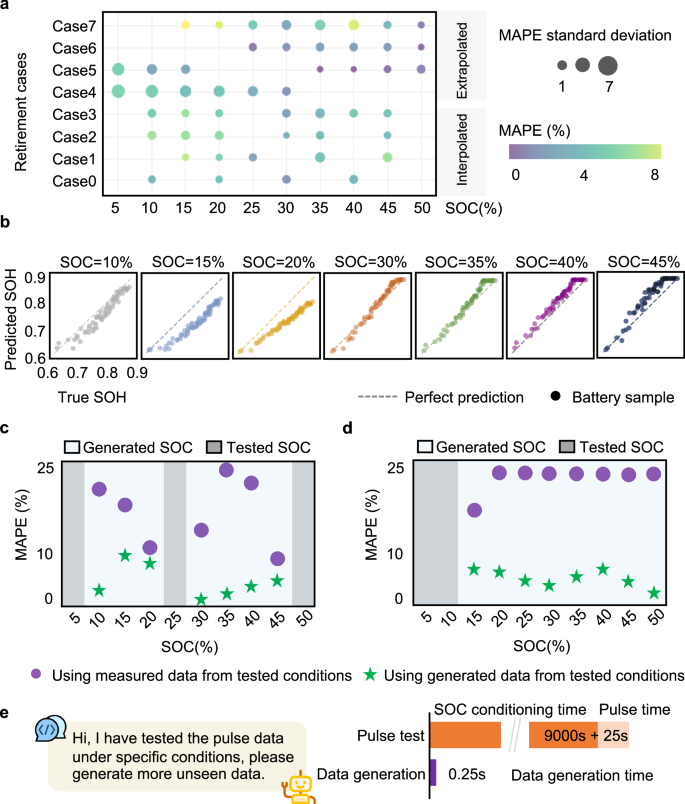
我们使用生成的脉冲电压响应特征来估计退役电池的 SOH。如图所示 4a，说明了不同电池报废情况下的 SOH 估计性能，其中阴影散点和空白区域分别代表生成模型的测试和训练条件。以案例3为例，在5%、25%和50%下进行物理脉冲测量，用于训练生成模型。训练后的模型会生成 10%、15%、20%、30%、35%、40% 和 45% SOC 的未见数据，用作回归器的输入数据，以实现这些未见 SOC 水平的 SOH 估计。尽管数据稀缺，我们证明生成的数据成功地促进了准确的 SOH 估计，在解释性和外推性情况下，平均 MAPE 和标准差分别为 4.9% 和 2.9%。然而，与外推生成相比，内插数据生成导致更准确和稳定的估计。插值情况下的平均 MAPE 和标准差分别为 4.4% 和 2.5%；外推情况下的平均 MAPE 和标准差分别为 6.0% 和 2.7%。然而，这种现象可以通过 OOD 问题中的挑战来合理化，这要归功于将先验知识整合到潜在空间缩放中，请参阅“方法”。选定 SOC 值下的 SOH 估计结果如图 1 所示。 4b带有奇偶校验图，表明在广泛的 SOC 条件下成功生成了数据。

不同情况下的SOH估计性能如图1所示 3c。乙案例 3 中真实 SOH 和估计 SOH 的奇偶图，即使用在 5、25、和 50% SOC。c使用测试条件下的可用数据（灰色阴影区域）与案例 3 中生成的数据进行 SOH 估计比较。d使用测试条件下的可用数据（灰色阴影区域）与案例 7 中生成的数据进行 SOH 估计性能比较。e在所需 SOC 级别的脉冲测试之间检索未见过的数据的时间成本比较41^{生成学习辅助数据生成。}所有结果均来自 NMC、2.1 安时电池以供说明。源数据作为源数据文件提供。

在这里，我们比较了有数据生成和没有数据生成的 SOH 估计结果，强调了其在高度随机退休条件下的必要性。如图所示 4c，解释性案例显示某些离散 SOC 值中的数据访问有限，由灰色阴影区域表示。使用这些数据，回归器会产生偏向于可用数据分布的质心的不准确估计，平均 MAPE 为 17.3%，标准差为 7.3。相比之下，生成学习辅助的 SOH 估计显示出大幅增长。平均 MAPE 为 5.4%，标准差为 2.7，如图中的星号所示。我们观察到在较高和较低 SOC 区域下对 SOH 的有趣高估和低估，这可以通过其潜在空间中的零均值和单位方差高斯分布来解释（参见“方法”）。具体来说，以低估为例，在低 SOC 区域条件下生成的脉冲电压响应表现出较高的值，否则表现为具有较低 SOH 的电池退化程度更高，反之亦然。⁶³。该观察结果具有重要意义，即可以通过操纵潜在空间来调整数据生成模型，以生成不可见但有条件的数据。

我们考虑一种极端但更优选的情况，其中可访问的数据可以位于低 SOC 区域。这种情况具有明确的物理意义，即这些区域中的数据管理可以最大限度地减少 SOC 调节时间。然而，数据管理策略尽管节省了管理时间和成本，但给准确估计带来了更多困难。如图所示 4天，我们以5％和10％SOC的可访问数据进行插图。当使用可访问的数据进行SOH估计时，它清楚地显示了渐近增加的误差。渐近效应可以解释为从可访问的数据分布随着SOC值的增加而增加，并遵守图中的观察。 2d。在低社会区域中使用数据时，这种挑战导致平均MAPE为23.8％，标准偏差为7.3。相比之下，使用生成的数据，估计性能提高到6.0％的MAPE和2.9的标准偏差。其他退休电池的估计结果（具有不同的阴极材料类型，物理格式和历史使用模式）始终如一地改进，请参见补充图。 18。因此，生成学习通过在SOC调理所要求的否则要求的SOC条件下生成在看不见的SOC条件下的数据来赋予对退休电池的快速预处理⁴¹，因此以数据驱动的方式推进了有效且可持续的电池重复使用和回收。

技术经济环境评估

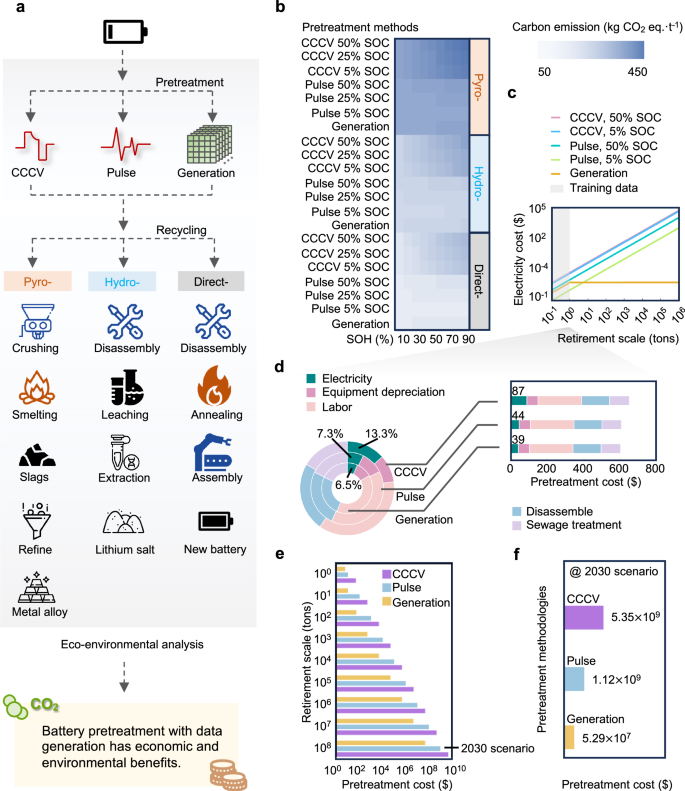
对SOH估计的技术 - 经济环境评估，包括传统的CCCV容量校准测试，支持脉冲测试的机器学习方法以及提出的生成学习辅助SOH估计方法。技术经济环境评估的边界包括从退休电池进入预处理阶段，从回收方法中进行选择，并以对经济和环境影响的评估结束的整个过程。尽管在图2中呈现了高温铝，水透明和直接回收的差异。 5a，退休的电池预处理是确定回收潜在资本回报的常见步骤。预处理与充电和排放电池的电力成本有关，而回收过程与材料投入，电力成本，设备折旧，人工，拆卸和污水处理有关。

对载铝（Pyro-），湿润铝（Hydro-）和直接回收的预处理方法的比较。乙一氧化碳2_{在不同的健康状态（SOH）和电荷状态（SOC）下，使用不同的预处理方法对预处理和回收的排放评估。}c使用直接回收在80％的SOH时对电池退休量表进行的电力成本进行比较分析，在后训练阶段的脉冲电力排除在外。d总体成本分析，不包括使用不同预处理方法的材料流，假设面板中的灰色阴影区域表示1吨的退休电池量表，以下是80％SOH和50％SOC（c）。e在电池退休量表上进行预处理成本，假设有80％的SOH和50％的SOC，则包括训练后阶段的脉搏电力包括在训练后阶段的电力。f在2030年电池退休方案中，详细的预处理成本。包括模型部署阶段的脉冲电力。著名的值代表每种方法的绝对成本。控制板 （一个）是使用flaticon.com创建的。源数据作为源数据文件提供。

每吨退休电池的利润和碳足迹是功能单位。我们检查了两种普遍的阴极材料类型，即NMC和LFP，以确定材料投资和收入，并提供了补充注释中的详细方法。3。我们显示了在图2中预处理退休的NMC电池的环境优势。5bâg，经济利益的结果在补充图中给出了。 19。在补充图中显示了预处理的退休LFP电池的结果。 20,21。由于数据短缺和回收例程中的不确定性，对退休LMO电池的分析未涵盖。在图 5b，高压铝表现出最高的CO₂排放，然后是水均能和直接回收。一氧化碳₂使用CCCV的排放量，在高温铝，水透明和直接回收中为1104-，729-和579千克等式。每吨退休的NMC电池分别假定退休SOH和SOC条件的80％和50％。我们发现，通过我们的生成学习辅助SOH估计2_{排放量减少到753-，379和228公斤等式。}每吨退休的NMC电池。除了CO2_{排放，使用相同预处理的电力成本在补充图中。} 19和20分别用于NMC和LFP退休电池。补充图 22和23显示出清晰的趋势，保存了CO₂SOH的排放和成本增加，尤其有利于促进电力和回收投资的减少。将来，随着可再生能源渗透的增长，评估的碳排放效果将增加。电价的上涨将导致经济利益的上涨。

在图 5c，我们通过对电池退休量表进行比较分析，以80％的SOH进行电池退休量表，阐明了有效预处理的影响，不包括训练后培训阶段的脉冲注入电力成本。在1.07吨退休量表上，生成学习成本低于SOC 25％的退休电池的脉搏测试，这是成本上第二好的预处理方法。在5.33吨退休量表上，生成学习的成本低于脉冲测试的脉搏测试，该电池的SOC为5％，确定它是最佳的。此外，生成学习的优势不依赖于退休电池的退休量表，当时电池超过5.33吨，适合大规模退休电池处理。保守地估计，从1吨退休电池（25,500个18650电池样品）收集的数据足以监督数据生成模型。但是，我们的模型仅使用此类培训数据量表的10.6％（2700个样本），这表明数据生成的模型培训成本仍然可以进一步降低到低于\（5.7 \ times {10}^{ - 3} \）美元。

由于其成本敏感性，直接回收被选择进行评估。我们分析了降低电力成本对整体成本比例的影响。在图 5天，示出了预处理成本的环和堆叠条图，以显示1吨退休电池的电力消耗的变化，分别具有相对和绝对值，不包括材料流。当退休条件在80％的SOH和50％SOC时，与传统的CCCV容量校准测试相比，使用故意数据生成的电力消耗比例从13.3％降至6.6％。绝对电力成本包括预处理和回收过程，从80吨减少到每吨退休电池。使用生成学习辅助的SOH估计可以在补充图中找到对退休LFP直接回收的总体影响。 24。如图所示，考虑到2030年的电池退休场景 5e，预处理电力储蓄随着退休缩放而呈指数增长\（{10}^{9} \）美元级别。在图 5f，生成学习可节省49亿美元的电力成本，并减少358亿公斤的CO₂与传统的基于CCCV的容量校准测试相比，排放量，请参见补充图。 25。关于LFP电池，可以在节省电力成本中观察到类似的比例效应，并且CO₂在2030年的情况下减少排放，请参见补充图。 26Ø27 号。节省成本和合作₂减少排放并不仅仅源于直接回收的优先级，更重要的是，使用拟议的生成学习辅助的SOH估计，在随机退休条件下保存详尽的数据策展。

我们已经阐述了使用生成学习来生成退休电池的高保真脉冲电压响应数据的成功，同时节省了调理成本和时间。成功归因于生成模型学习退休条件与脉搏电压响应之间的依赖性，包括阴极材料类型中的异质性，物理格式，容量设计和历史用法，请参见补充图。 28。使用能力校准测试与传统的SOC调节差异，甚至最先进的脉冲测试与特定SOC级别的机器学习结合⁴¹，提议的数据生成模型强调了利用已经测量的数据和使用随机SOH和SOC退休条件探索潜在的数据空间之间的平衡。拟议的方法没有进行额外的身体测量，从而减少了次要能源使用和实际使用中的环境负担。借助一部分生成的数据，下游SOH估计任务仍然与足够的数据情况相比，仍然始终如一地执行，这是降低计算成本和改善现实情况下的估计准确性的有用含义，请参见补充图。 29Ø32。在补充讨论中可以找到有关该方法进步的讨论，包括模型解释性，电池回收的含义以及机器学习集成的电池重用和回收预处理的灵感，可以在补充讨论中找到。

总之，拟议的生成学习证明了在迅速，准确和可持续的估算退休电池的SOH方面的合并承诺。我们提出了一个由一些物理测量的脉冲电压响应数据监督的生成学习模型，该模型可以有效地在宽阔的SOC和阴极材料类型上生成新数据，而解释性和外推病例的绝对百分比误差平均低于2％。使用生成的数据，回归器的平均绝对百分比误差低于6％的SOH估计，包括看不见的SOC条件。结果通过3种流行的阴极材料类型（NMC，LFP和LMO），3种物理格式（圆柱，小袋和棱镜），4种容量设计（2.1、10、21和35 AH）和4种验证。历史用法（1个实验室加速衰老和3种不同的EV驾驶衰老模式）。我们通过节省49亿美元的电力成本并减少358亿公斤的CO，在全球范围内的电池退休场景中展示了数据生成的经济和环境可行性。2_排放。通常，提议的数据生成方法可实现可持续的电池重复使用和回收决策⁶⁴，特别是用于直接回收，通过设计适当使用锂补充剂和其他化学试剂，对回收成本和产品质量至关重要。从广义上讲，生成学习方法激发了利用已经测量的数据以探索无穷无尽的数据空间的承诺，而不是单独的物理测量，减轻了数据稀缺性和在关键估计中的数据稀缺和异质性问题，在数据和预测应用程序中，数据是昂贵，昂贵，昂贵，昂贵，昂贵的，昂贵的，并污染以取回。

跨注意机制

神经网络中的跨注意力使模型可以专注于一个输入的特定部分，即基于另一个输入中的信息，即键和值。在一个数据流中某些功能的相关性取决于提供的其他信息，并且在电池健康诊断和预后中已成功应用，这很有用^65,66,67,68。在电池回收预处理中，退休的电池在随机退休条件下，即电荷状态（SOC）分布。从专家知识中，脉冲电压响应与SOC表现出相当大的转变。因此，交叉注意力可以探索脉冲电压响应与SOC退休条件之间的条件依赖性。跨注意机制的一般表述是：

在哪里，\（q，k，v \）分别表示查询，键和值序列。\（{d} _ {k} \）是缩放因子，通常是密钥的维数值\（k \）。\（T \）是转置操作员。这\（{{{\ rm {softmax}}}}} \）功能使输入向量归一化，因此概率的总和为1，使计算的注意力成为有效的概率分布。在跨注意中\（{{{\ rm {softmax}}}}} \）用于计算代表输入序列中不同元素的重要性的权重。给定一个向量\（{{{{\ bf {v}}}}} = [{v} _ {1}，{v} _ {2}，\ bulter \ bulter \ bullet \ bullet，{v} _ {p} _ {p}] \）\）实际数字，\（{{{\ rm {softmax}}}}} \）函数为\（我\） - 该向量的元素由以下方式给出：

其中分母是所有元素的指数总和\（{V} _ {i} \）在矢量中\（{{{\ bf {v}}}}} \）,\（i = 1，\ ldots，p \）。\（p \）是向量中的元素数量\（{{{\ bf {v}}}}} \）。

具有跨注意的编码器神经网络

变性自动编码器中的编码器网络旨在将输入数据压缩到潜在空间中。首先采用21维电池电压响应功能矩阵\（{{{{\ bf {x}}}}} \ in {{\ mathbb {r}}}}}}^{n \ times 21} \）作为主要输入和退休条件矩阵\（{{{{\ bf {cond}}}}} = [{soc}，{soh}] \ in {{\ mathbb {r}}}}}}作为输入，哪里\（n \）是样本大小。条件输入首先转换为嵌入\（{{{\ bf {c}}}}} \），属于具有64个维度的较大潜在空间。条件嵌入\（{{{\ bf {c}}}}} \）公式为：

在哪里，\ \（{{{{{\ bf {w}}}}}}} _ {{{{{\ bf {{c}}}}}}}} \ in {{\ mathbb {r}}}}}}}}}}}^{64 \ times 2}{{{\ bf {b}}}}}} _ {{{{{{\ bf {c}}}}}}}}}}} \ in {{\ MathBB {r}}}}}}}}次64} \）是嵌入神经网络加权矩阵和偏置矩阵的条件。

主要输入矩阵\（{{{\ bf {x}}}}} \），代表脉冲电压响应特征，也转化为这个64维的潜在空间\（{{{\ bf {h}}}}} \）:

在哪里，\ \（{{{{{\ bf {w}}}}}}} _ {{{{{{\ bf {h}}}}}}}} \ in {{\ mathbb {r}}}}}}}}}}}^{64 \ times 21}{{{\ bf {b}}}}}} _ {{{{{{\ bf {h}}}}}}}}}}}} \ in {{\ Mathbb {r}}}}}}}^次64} \）分别是嵌入神经网络加权矩阵和偏置矩阵的主要输入。

两个都\（{{{\ bf {h}}}}} \）和\（{{{\ bf {c}}}}} \）然后通过跨注意集成，使网络专注于电压响应矩阵\（{{{\ bf {x}}}}} \）以其他退休条件信息为条件\（{{{\ boldsymbol {cond}}}}} \）:

在哪里，\ \（{{{{\ bf {h}}}}}} \ in {{\ MathBb {r}}}}}}}^{{{{{\ rm {n}}}}}}} \ times 64} \ \）和\ \（{{{\ bf {c}}}}}} \ in {{\ Mathbb {r}}}}}}}^{{{{{\ rm {n}}}}}}}} \ times 64} \ \）分别是脉冲电压响应数据和退休条件数据的嵌入。\ \（{{{{\ bf {attenencoder}}}}}}} \ in {{\ Mathbb {r}}}}}}^{{{{{\ rm {n}}}}}}} \ times 64} \）\）是嵌入电压响应的交叉量输出矩阵\（{{{\ bf {h}}}}} \）和退休条件嵌入\（{{{\ bf {c}}}}} \）。

\（{{{{{\ bf {z}}}}}}} _ {{{{{{\ bf {sean}}}}}} \）和\ \（{{{{{\ bf {z}}}}}}} _ {{{{\ log}}} \ _ {{{{\ bf {var}}}}}}}}}}} \）构成每个高斯分布\（l = 2 \）维度潜在空间：

在哪里，\ \（{{{{{\ bf {z}}}}}}}} _ {{{{{{\ bf {sean}}}}}}}}} \ in {{\ mathbb {r}}}}}}}}}^{{{{{{{{{}}}} \ times {{{\ rm {l}}}}}}} \）\）,\ \（{{{{{\ bf {z}}}}}}}} _ {{{{\ log}}} \ _ {{{{{{\ bf {var}}}}}}}}}}}}}}}}}}{{{{\ rm {n}}}}} \ times {{{\ rm {lm {l}}}}}}}} \）\）是高斯分布方差的平均值和对数。\ \（{{{{{{\ bf {w}}}}}}} _ {{{{{{{{\ bf {Z}}}}}}}}}}}}}} _ {{{{{\ bf {\ bf {sane}}}}}}}}}}}}}}}}}} \ in {{Mathbb {r}}}}^{{{{{\ rm {l}}}}}} \ times 64} \）,\ \（{{{{{{\ bf {b}}}}}}}} _ {{{{{{{{\ bf {Z}}}}}}}}}}}} _ {{{{{\ bf {\ bf {sane}}}}}}}}}}}}}}}}}} \ in {Mathbb {r}}}}^{{{{{\ rm {n}}}}}} \ times {{{\ rm {lm {l}}}}}}} \）分别是可训练的加权矩阵和偏置矩阵。\ \（{{{{{\ bf {w}}}}}}}} _ {{{{{{{{\ bf {Z}}}}}}}}}}}} _ {{{\ log}}}}}}}}}}} \ in {{\ Mathbb {r}}}}}^{{{{{\ rm {lm {l}}}}}} \ times 64} \）,\ \（{{{{{\ bf {b}}}}}}}} _ {{{{{{{{\ bf {Z}}}}}}}}}}}} _ {{{\ log}}}}}}}}}}}}} \ in {{\ Mathbb {r}}}}}^{{{{{\ rm {n}}}}}} \ times {{{{\ rm {lm {l}}}}}}}}}}}}}}} \）分别是潜在空间方差嵌入的神经网络加权矩阵和偏置矩阵。

潜在的空间扩展以先验知识告知

某些退休条件，例如，由于数据稀缺或测量预算，电池回收预处理中的极端SOH和SOC的代表性不足。具体而言，退休的电池表现出集中的SOH和SOC，在面对分发电池（OOD）电池时，估计性差。由于仓库存储需求的安全问题，收集的退休电池的放电低于一定电压阈值，导致高限SOC通常低于50％。即使明确的电池退休条件仍然未知，我们也可以使用此近似的先验知识来生成足够的合成数据以涵盖实际的退休条件。鉴于两个数据生成设置，即插值和外推，我们使用不同的潜在空间缩放策略。在插值设置中，缩放矩阵\（{{{{\ bf {t}}}}}} \ in {{\ Mathbb {r}}}}}}}^{{{{{{\ rm {n}}}}}}}}}}}}}\)是一个身份矩阵\ \（{{{\ bf {i}}}}}} \ in {{\ Mathbb {r}}}}}}}}^{{{{{\ rm {n}}}}}}}}}}}}}}\)假设编码器网络和解码器网络可以在不利用任何先验知识的情况下学习继承的数据结构。但是，在推断设置中，由于OOD问题，这是机器学习模型的一般挑战，因此无法保证该假设。在这里，我们使用培训和测试SOC分布的手段来定义缩放矩阵以及对电池退休条件的先验知识，然后将潜在空间缩放为：

在哪里，\ \（{{{{{{\ bf {t}}}}}}}} _ {{{{{{\ bf {sean}}}}}}}}} \ in {{\ mathbb {r}}}}}}}}}}}} \ times {{{\ rm {n}}}}}}} \）和\ \（{{{{{\ bf {t}}}}}}}} _ {{{{\ log}}} \ _ {{{{{\ bf {var}}}}}}}}}}}}}}}}}}}{{{{\ rm {n}}}}} \ times {{{\ rm {n}}}}}}} \）\）是由广播平均值定义的缩放矩阵，分别是测试和培训SOC分布之间的差异比率。我们强调的是，SOH分布与这样的扩展无关。这是因为这些相同的SOH值可以看作是代表物理上不同的电池，即它们不影响缩放过程。因此，在训练和重建过程中以相同的SOH值喂养模型不会出现OOD问题。另一方面，对于SOC维度，我们的目标是在无法用尽物理测试的情况下生成数据。

在缩放的潜在空间中采样

VAE中的采样步骤是编码器神经网络的确定性输出与缩放潜在空间的随机性质之间的桥梁。它允许模型捕获输入数据的隐藏结构，特别是脉冲电压响应\（{{{\ boldsymbol {x}}}}} \）\）和\（{{{\ boldsymbol {cond}}}}} \）探索类似的数据点。采样程序可以表达为：

在哪里，\ \（{{{{\ boldSymbol {\ epsilon}}}}}}}} \ in {{{\ MathBb {r}}}}}}}^{{{{{\ rm {n}}}}}}}}}}}}}}}}}} \ times {}} \），是从中采样的高斯噪声矢量\ \（{{{\ boldsymbol {\ epsilon}}}}}}}}}}}}} \ sim {{{\ boldsymbol {{{{{{\ mathscr {n}}}}}}}}}}}}}}}}}}}}}}}}}}（{{{{\ bf {0}}}}}}}{{{{\ bf {i}}}}}）\）。指数项\ \（{{{{{\ rm {e}}}}}}}}}}^{\ frac {1} {2} {2} {2} \ cdot {{{{{\ bf {z}}}}}}}}}}}}}}}}}}} _ {{{{{\ bf {var}}}}}}} \）将对数方差向量变成正方差向量。\（{{{{\ bf {z}}}}}} \ in {{\ Mathbb {r}}}}}}}^{{{{{{\ rm {n}}}}}}}}}}}}}}\)是采样的潜在变量。

交叉注意的解码器神经网络

解码器网络转换采样的潜在变量\（{{{\ boldsymbol {z}}}}} \）\）返回原始数据台带，重建输入数据或生成有关原始或看不见的退休条件的新数据。解码器的第一步是一个致密的层，可转换\（{{{\ boldsymbol {z}}}}} \）\）进入中间表示：

在哪里，\ \（{{{{{\ bf {w}}}}}}} _ {{{{{\ bf {d}}}}}}} \ in {{\ Mathbb {r}}}}}}}}^{64 \ times {64 \ times {64 \ \ rmm{l}}}}}} \）\）,\ \（{{{{{\ bf {b}}}}}}}} _ {{{{{\ bf {d}}}}}}}} \ in {{\ mathbb {r}}}}}}}}}}}} \ times 64} \）\）分别用于潜在变量解码嵌入的神经网络加权矩阵和偏置矩阵。\ \（{{{{{\ bf {h}}}}}}}}}^{{{{{{\ prime}}}}}}} \ in {{\ mathbb {r}}}}}}}}\ times 64} \）是嵌入式潜在变量。

\（{{{{{\ bf {h}}}}}}}}^{{{{{\ prime}}}}} \）然后通过跨注意集成，允许网络专注于电压响应矩阵的相关方面\（{{{\ bf {x}}}}} \）由额外的退休条件嵌入\（{{{{{\ bf {c}}}}}}}}^{{{{{\ prime}}}}} \）\）:

在哪里，\ \（{{{{{\ bf {h}}}}}}}}}^{{{{{{\ prime}}}}}}} \ in {{\ mathbb {r}}}}}}}}\ times 64} \）和\ \（{{{{{\ bf {c}}}}}}}}}}}^{{{{{\ prime}}}}}}} \ in {{\ Mathbb {r}}}}}}}}}\ times 64} \）分别是嵌入的潜在变量和退休条件嵌入。\ \（{{{{\ bf {aptheCodeder}}}}}}} \ in {{\ MathBb {r}}}}}}^{{{{{\ rm {n}}}}}}} \ times 64} \）\）是来自嵌入式潜在变量的跨意见输出矩阵\（{{{{{\ bf {h}}}}}}}}^{{{{{\ prime}}}}} \）和退休条件嵌入\（{{{{{\ bf {c}}}}}}}}^{{{{{\ prime}}}}} \）\）。训练时，我们让\ \（{{{{{\ bf {c}}}}}}}}}^{{{{{\ prime}}}}}} {=} {=} {{{\ bf {c}}}}}}}}}}} \），解码器重建输入脉冲响应数据。生成新数据时，\（{{{{{\ bf {c}}}}}}}}^{{{{{\ prime}}}}} \）\）是要生成的新数据的SOH和SOC条件。重建（生成）数据\ \（\ hat {{{{{\ bf {x}}}}}}}} \ in {{\ Mathbb {r}}}}}}^{{{{{\ rm {n}}}}}}}}}}}}}}}}}}}计算如下：

在哪里，\ \（{{{{{\ bf {w}}}}}}} _ {{{{{\ bf {o}}}}}}} \ in {\ in {\ mathbb {r}}}}}},\ \（{{{{{\ bf {b}}}}}}}} _ {{{{{\ bf {{o}}}}}}}} \ in {{\ mathbb {r}}}}}}}}}^{{{{{{{{}}}} \ times 21} \）\）分别用于输出转换的神经网络加权矩阵和偏置矩阵。\（\ sigma \）是Sigmoid激活函数。

损失函数

损失函数包括两个部分，即重建损失和kullback-leibler（KL）差异损失。重建损失，即均方根误（MSE）损失\（{{{Loss}} _ {{MSE}} \）\）在原始和重建（生成）数据之间，是：

在哪里，\ \（{{{{{\ bf {x}}}}}}} _ {{{{{\ bf {i}}}}}}}} \ in {{\ mathbb {r}}}}}}和\ \（{\ hat {{{{{\ bf {x}}}}}}}} _ {{{{\ bf {\ bf {i}}}}}}}} \ in {{\ Mathbb {r}}}}}}}}}}}}}}^{1 \ times times times times times times times times 21}\)分别是每个样品中的原始和重建（生成）脉冲电压响应数据。\（n \）是样本大小。

KL差异损失\（{{{损失}} _ {{kl}} \）\），即原始数据和生成数据之间的KL差异为：

总损失是线性组合\（{{{Loss}} _ {{MSE}} \）\）和\（{{{损失}} _ {{kl}} \）\）:

在哪里，\（{{{{{\ rm {\ omega}}}}}}}} _ {{{{{\ rm {xent}}}}}}} \）和\（{{{{{\ rm {\ omega}}}}}}}} _ {{{{{\ rm {kl}}}}}} \）设置为0.5，以分别在发电准确性和多样性之间达到平衡⁶⁹。\（n \）是样本大小。

随机森林回归者

由于脉冲电压响应曲线的特征工程后，我们采用随机森林算法进行SOH估计，因此可以表达为：

在哪里\（\ bar {{{{{\ bf {y}}}}}}} \）是预测的SOH值向量。\（M \）是随机森林中的树号。\（{{{{\ boldsymbol {\ vartheta}}}}}}}} _ {{{{\ rm {m}}}}}}} \）和\（{{{{\ boldsymbol {\ theta}}}}}}}} _ {{{{\ rm {m}}}}}}} \）是超参数，即最小叶子大小和最大深度\（{{{\ rm {k}}}}} \）随机森林中的树。在不同情况下，超参数设置为相等的，即\（{{{\ rm {m}}}}} = 20 \）,\（{{{{\ boldsymbol {\ vartheta}}}}}}}}} _ {{{{\ rm {m}}}}}} = 1 \）， 和\（{{{{\ boldsymbol {\ theta}}}}}}}} _ {{{{\ rm {m}}}}}} = 64 \），进行公平的比较。实现在Python 3.11.5环境中的Sklearn软件包（1.3.1版）中，随机状态为0。

评估指标

平均绝对百分比误差定义为：

在哪里，\（{人工智能}\）和\（{f} _ {i} \）分别是实际和估计值。\（n \）是样本大小。

报告摘要

有关研究设计的更多信息可在自然投资组合报告摘要链接到本文。

作者笔记

1. These authors contributed equally: Shengyu Tao, Ruifei Ma, Zixi Zhao.

作者和单位

1. Tsinghua-Berkeley Shenzhen Institute, Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen, China

   Shengyu Tao, Ruifei Ma, Zixi Zhao, Guangyuan Ma, Lin Su, Heng Chang, Yuou Chen, Haizhou Liu, Zheng Liang, Tingwei Cao, Haocheng Ji, Zhiyuan Han, Guodan Wei, Yang Li, Xuan Zhang & Guangmin Zhou

2. State Key Joint Laboratory of Environment Simulation and Pollution Control (SKLESPC), School of Environment, Tsinghua University, Beijing, China

   Minyan Lu & Zongguo Wen

3. Xiamen Lijing New Energy Technology Co., Ltd., Xiamen, China

   Minyan Lu & Huixiong Yang

4. Tencent AI Lab, Tencent, Shenzhen, China

   Jianhua Yao & Tingyang Xu

5. DAMO Academy, Alibaba Group, Hupan Lab, Hangzhou, China

   容宇

贡献

英石。conceptualized, designed, and implemented the numerical experiments.R.M.contributed to the techno-environmental analysis.Z.Z.discussed and implemented part of the experiments.G.M., L.S., Y.C., and Z.L.preprocessed the measured data;H.C., H.L., and Z.H.discussed the work;T.C.prepared the artistic works;H.J. contributed to scientific issues of battery recycling pretreatment;M.L., H.Y., Z.W., and G.W.supported data curation;J.Y., Y.R., Y.L., and T.X., reviewed and discussed the work;X.Z.and G.Z.conceptualized, reviewed, discussed, supervised this work and retrieved fundings.

通讯作者

通讯至张旋,徐廷阳或者周广民。

利益竞争

作者声明没有竞争利益。

同行评审信息

自然通讯thanks Lluc Canals Casals, Sarang D. Supekar, Siby Jose Plathottam, Daniela Chrenko, and the other anonymous reviewer(s) for their contribution to the peer review of this work.同行评审文件可用。

开放获取本文获得 Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License 的许可，该许可允许以任何媒介或格式进行任何非商业使用、共享、分发和复制，只要您给予原作者适当的署名即可和来源，提供知识共享许可的链接，并指出您是否修改了许可材料。根据本许可，您无权共享源自本文或其部分内容的改编材料。The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.要查看此许可证的副本，请访问http://creativecommons.org/licenses/by-nc-nd/4.0/。转载和许可

关于本文