从头算机器学习揭示了钨非阿伦尼乌斯自扩散的强非和谐性

了解原子扩散对于开发具有受控机械和功能特性的材料至关重要。对于大多数金属，热激活、空位介导的扩散的温度依赖性已通过无数研究得到了很好的评估。众所周知，阿累尼乌斯行为是线性的。磁的^1,2, 化学有序无序^3,4，或结构⁵转换可能会导致阿累尼乌斯型温度依赖性的特征偏差。当相变不干扰时，扩散速率的对数，D，假设与温度倒数成线性比例，时间^Ø1,

随着坡度， 问/k_乙，和截距，\({{\rm{\ln }}}{D}_{0}\)，由活化能控制问和前因子D₀(k_乙：玻尔兹曼常数）。两个都问和D₀一般假设为独立的或对温度的依赖性非常弱⁶。

然而，这种广泛假设的普遍性是有限的，特别是接近熔点时⁶。扩散测量覆盖宽的温度区间揭示了线性偏差^{7,8,9,10,11,12}。教科书知识解释了除了单空位之外还存在双空位的替代扩散的“异常现象”^6,13,14。各种测量^{15,16,17 号}被解释为支持双空位解释，该解释已成为无可争议的范式。尽管如此，一些研究人员提出了一种与温度相关的活化能的替代解释^{18,19,20,21,22}即使在简单金属中，也表明单/双空位解释存在问题。最近的从头算模拟确实揭示了由非谐振动驱动的与温度相关的空位形成能^23,24。还发现 Mo 中的自扩散与温度相关的空位能²⁵。

这些理论发现需要对长期存在的范式进行概念性修正。然而，范式转变需要强有力的支持。因此，不仅需要对缺陷能量学进行进一步的从头开始模拟，而且特别需要在方法上取得进展，以便能够在高温下获得可靠的预测。

虽然高效的高精度从头算技术可用于空位形成^23,26，最先进的从头算方法通过（准）调和过渡态理论（hTST）近似迁移吉布斯能量²⁷，利用全准谐波自由能²⁸或简化的葡萄园公式²⁷具有显式声子计算²⁹。下面将表明，hTST 在高温下是不现实的，并且会导致严重的错误。

探索完整振动空间的最准确方法是热力学积分。热力学积分的一个关键要求是“足够的”相稳定性，即目标相应该在感兴趣的温度范围内动态稳定。某些相关的晶格不稳定性，例如，观察到 hcp Ni 的 hcp 到 dhcp 转变³⁰，通过增加模拟单元的大小来抑制。通过将细胞限制为较小的尺寸可以抑制其他不需要的转化³¹。对于扩散原子在高能鞍点处经历的本质上局部不稳定性，此类措施不会有效。尽管基于有限温度路径的方法（例如有限温度弦方法）³²以及基于平均力的积分^33,34虽然已经开发出包括对激活自由能的全部振动贡献，但它们在从头算框架中的实际应用并不简单。

在这里，我们提出了一种有效且准确的从头计算方法，克服了过渡态的动力学不稳定问题。我们证明，通过引入稳定方案（在机器学习辅助热力学积分 + 直接上采样框架中实现），可以有效计算空位迁移吉布斯能量的完整温度依赖性，包括与密度相关的所有热激发泛函理论（DFT）的准确性。与空位形成吉布斯能量一起，同样可以通过直接上采样技术计算，即使对于高熔点系统，也可以获得精确的从头算自扩散率。

过渡态热力学积分

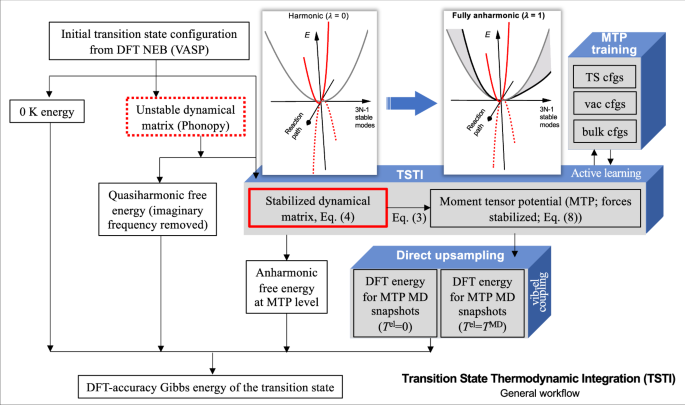
图 1提供了所介绍的一般工作流程过渡态热力学积分（TSTI）方法。关键部分用灰蓝色框突出显示。核心在于从稳定的动态矩阵到高度优化的机器学习潜力的实际 TSTI 计算，特别是矩张量潜力 (MTP)³⁵。TSTI 计算之后直接上采样以实现 DFT 精度。

所提出的过渡态热力学积分 (TSTI) 方法的示意图（NEB = 微移弹性带；TS = 过渡态；cfgs = 配置（从 MD 采样）；时间埃尔=电子温度）。^{MTP 在大型 DFT 数据集（2591 个结构）上进行训练，包括从高温 MD 采样的块体、空位和过渡态配置。}能量的均方根误差 (RMSE) 仅为 1.9 meV/atom，力的均方根误差 (RMSE) 仅为 0.15 eV/à。

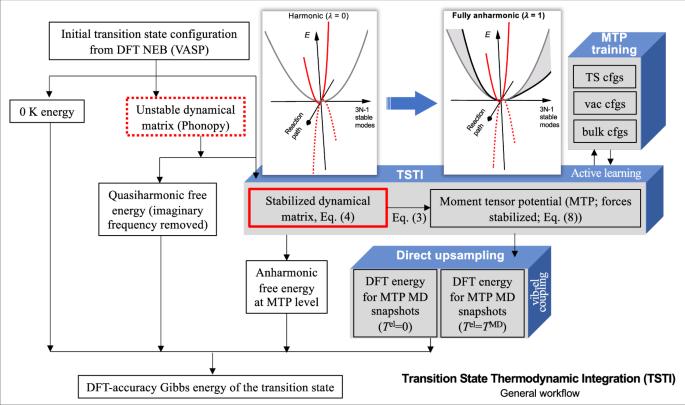
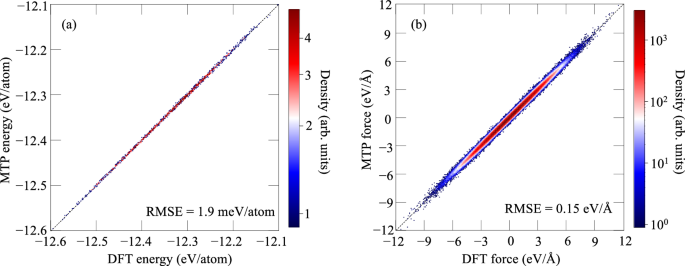
因此，MTP 预测的 MD 能量（总共 2591 个能量）和力（总共近 100 万个力）与 DFT 数据显示出很强的相关性，参见图。 2。MTP 的良好性能确保了对所考虑的体积、空位和过渡态配置的振动相空间的准确描述，并提高了直接上采样收敛性。有关 MTP 的更多详细信息请参阅“方法”部分。

能量的相关图（一个）和力（乙）的 MTP 与 DFT 以及相应的均方根误差 (RMSE)。非简谐自由能表示为

$${F}^{{{\rm{ah}}}}=\Delta {F}_{{{\rm{MTP}}}}^{{{\rm{qh}}}\到{{

其中第一项\(\Delta {F}_{{{\rm{MTP}}}}^{{{\rm{qh}}}\至{{\rm{完整}}}}\)由TSTI计算得到MTP和第二项\(\Delta {F}_{{{\rm{DFT}}}}^{{{\rm{up}}}}\)从自由能微扰理论，即直接上采样，到DFT。具体来说，

表示沿耦合参数的热力学积分我” Ø[0, 1]，用热力学平均值°。。。�_我”准谐波能量之间的差异乙^qh和稳定的全振动 MTP 能量\({E}_{{{\rm{s}}}}^{{{\rm{完整}}}}\)（下面讨论）针对原子坐标的不同配置计算{右_我}。对于每个固定的的值我”，MD 模拟中的原子运动是由准谐波力和 MTP 力的线性组合所产生的力驱动的。

这里提出的方法的一个关键要素是稳定的动力矩阵\(\underline{\underline{{{{\boldsymbol{{\mathcal{D}}}}}}_{{{\rm{s}}}}}}\)根据原始的不稳定动力学矩阵计算

在哪里

代表两个3氮� � 3氮对角矩阵，存储 3氮Ø 1 个稳定的声子频率Ï_我和单身稳定的分别为声子频率。通过取反应坐标频率的绝对值来实现稳定\({\omega}_{{{\rm{imag}}}}^{2}\)乘以可调参数α。我们设定α为 30，该值确保不稳定模式的最终稳定频率，\(\sqrt{\alpha | {\omega }_{{{\rm{imag}}}}^{2}| }\)，高于过渡态频谱的最高稳定频率。有关稳定参数的更多详细信息和测试α中提供了 补充信息。进一步在方程中。（4),\(\下划线{\下划线{{{\bf{w}}}}}\)是原始不稳定动力矩阵的特征向量矩阵。

我们方案的第二个关键因素是热力学积分过程中 MTP 力的稳定性。这是通过将沿不稳定模式的力替换为稳定的简谐力由下式给出\(\underline{\underline{{{{\boldsymbol{{\mathcal{D}}}}}}_{{{\rm{s}}}}}}\)。具体来说，对于给定的我”，原子间力的计算公式为

与力量\({{{{\mathcal{F}}}}}_{{{\rm{s}}}}^{{{\rm{qh}}}}\)对应于\(\underline{\underline{{{{\boldsymbol{{\mathcal{D}}}}}}_{{{\rm{s}}}}}}\)并与稳定的MTP部队\({{{{\mathcal{F}}}}}_{{{\rm{s}}}}^{{{\rm{完整}}}}\)计算由

在哪里\({{{{\mathcal{F}}}}}^{{{\rm{MTP}}}}\)是原始不稳定的 MTP 力，

与鞍点位置\(\{{{{\bf{R}}}}_{I}^{{{\rm{sp}}}}\}\)和归一化特征向量\({\hat{{{\bf{w}}}}}_{{{\rm{imag}}}}\)的不稳定声子模式。一致地，相应的MTP势能进入方程。（3) 计算为

在哪里乙^MTP是原始不稳定的MTP势能。

TSTI 工作流程依赖于并显着推进了已建立的平衡态高精度从头吉布斯能量计算框架³⁶。特别是，如图 2 中的两个示意图所示。 1，不稳定模式（红色虚线）驱动鞍点构型达到平衡，并不直接贡献过渡态的振动自由能。在任意 我”，不稳定性被对应于的稳定能量分布所取代\(\alpha | {\omega }_{{{\rm{imag}}}}^{2}|\)（红色实线）。由于沿热力学积分路径的稳定能量分布保持不变，因此反应坐标对方程式中的自由能差没有明确的贡献。（2）。（这与采样 (3氮�1) 稳定模式，尽管处于谐波状态。）通过与稳定模式的耦合实现稳定的间接影响很小，并且可以通过α参数（参见 补充信息）。TSTI 的稳定性对于将振动限制在鞍点附近至关重要，例如能够从所有其他区域采样非谐性（灰色阴影区域），3氮�1 种稳定模式（灰色或黑色曲线）。

通过 TSTI，可以在 MTP 的精度级别捕获过渡态的非谐性。基于分子动力学快照的上采样，具有完整的自由能公式\(\Delta {F}_{{{\rm{DFT}}}}^{{{\rm{up}}}}\)确保DFT的准确性。利用有限温度 DFT 在第二个上采样步骤中计算电子激发及其与原子振动的耦合^36,37。因此，可以在 DFT 精度水平上计算过渡态的全套自由能贡献。

空位形成和迁移的温度依赖性吉布斯能

我们使用 TSTI 来计算空位迁移的吉布斯能量G米格（_时间) 对于 BCC W。参考过渡状态配置，\(\{{{{\bf{R}}}}_{I}^{{{\rm{sp}}}}\}\)，是从攀爬图像微移弹性带获得的38方法在零开尔文条件下进行。^{在高温下，甚至接近熔点，MD 迁移轨迹表明，对于像 BCC 这样的对称晶体结构，迁移途径保持不变（参见补充图 1）。} 6以及相关的讨论）。对于复杂的分子系统³⁹，由于对称性限制较少，迁移路径可能会在高温下发生改变，这需要进行特殊分析，这超出了本文的范围。我们使用热力学积分+直接上采样的“标准”方案³⁶计算空位形成的吉布斯能量G形式（_时间）。以前，温度依赖性G形式_{BCC W 是通过拟合单个数据点得出的}40^{，我们现在研究密集温度网格的显式温度依赖性。}自扩散系数读数

其中 h 是普朗克常数。零压力下的晶格常数一个（₀时间）是从参考文献中报告的相对热膨胀（DFT 分子动力学）获得的。41^{并用 0 K 处的晶格常数重新调整，即 3.1723 ×，在此处计算（参见} 补充信息了解更多详情）。BCC 晶格上空位扩散的相关因子，f密件抄送，取值为0.7272₄₂。^{对于 DFT 计算，我们采用投影增强波 (PAW) 方法}43^{Perdew-Burke-Ernzerhof (PBE) 参数化中的广义梯度近似 (GGA)}44^{在 VASP 中实现}45^,46。方法部分给出了更多详细信息。

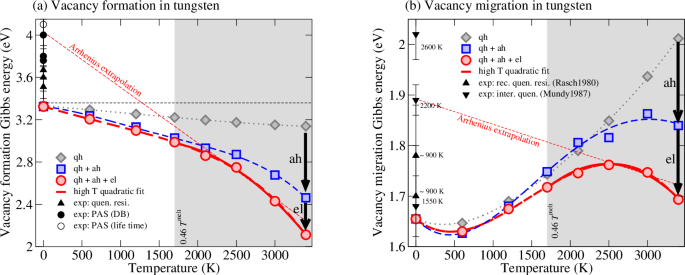
图 3表示 BCC W 的空位形成和迁移的温度依赖性吉布斯能量。红色圆圈和线对应于包含所有热贡献的最终吉布斯能量。对于两者G形式（_时间） 和G米格（_时间），强烈而清晰非线性观察到温度依赖性，特别是在测量扩散的温度范围内（时间>0.46时间熔化，灰色阴影区域）。^{计算出的高温数据通过二次拟合（红色实线）很好地再现了，正如之前对形成吉布斯能量所观察到的那样}23。^{对于空位形成，能量随温度的降低特别强烈，与 0 K 值相比，在 3400 K 时达到降低 1.21 eV（降低 36%）。}图 3：非谐性和电子对钨中空位形成和迁移的影响。一个

乙与实验相比，所提出的 TSTI 方法的迁移吉布斯能量（带有误差条的黑色符号显示实验不确定性）。实验技术：一个淬火电阻率74^{,75,76, 正电子湮灭能谱 (PAS) 多普勒展宽 (DB)77},^{78,79和一生的时间78};^乙淬火电阻率的恢复75和间断淬火²⁰。^{连接计算数据点（填充符号）的点划线是四阶多项式拟合。}红色虚线显示 2600 K 至 3000 K 温度范围内吉布斯能量的线性阿伦尼乌斯外推法。

实验数据（黑色符号）反映了利用高温测量的推断线性阿伦尼乌斯·安萨茨，即G_{表格/米格}= = H_{表格/米格}～ 时间S_{表格/米格}，具有与温度无关的焓（H_{表格/米格}）和熵（S_{表格/米格}）的形成/迁移。尽管根据当前和之前的结果，这种线性拟合 ansatz 显然是不合适的^23,24，我们仍然利用它来拟合我们的精确数据，以便在理论和实验之间进行公正的比较。对于形成和迁移，考虑到高温测量中的显着分散和不确定性，2600 K 和 3000 K 之间的全吉布斯能量的线性阿伦尼乌斯拟合显示出与实验的合理一致。

通常应用的准调和近似（灰色菱形）与具有全振动特征的吉布斯能量（蓝色方块）之间的比较揭示了空位形成和迁移中的强非和谐性。由于明显的不和谐性，吉布斯能量显着降低，如标记为“啊”的箭头所突出显示；最大限度。空位形成 20%，迁移 10%。对于全振动吉布斯能量观察到的强非线性温度依赖性在准调和近似中不存在。请注意，迁移吉布斯能是通过过渡态吉布斯能与空位超晶胞的差值获得的。因此，在图 1 中观察到的非谐波贡献。 3b 意味着与块体相比，过渡态甚至比已经强非简谐振动的空位超晶胞更非简谐振动。这凸显出迄今为止成熟且普遍应用的准谐波近似不足以描述空位介导的扩散中的振动贡献。

电子激发的强烈影响

传统上，电子激发被认为在最先进的扩散研究中影响较小²⁹。因此在实践中，电子自由能的显式计算经常被省略^29,47,48或者，在考虑时，依赖于理想的静态晶格近似⁴⁹。

目前的计算框架使我们能够明确地解释电子激发以及与热振动的耦合效应。如图所示 3，包括振动耦合在内的电子激发对吉布斯能量提供了相当大的贡献（标有“el”的黑色箭头）。空位形成相应降低 0.35 eV，迁移吉布斯能相应降低 0.15 eV。

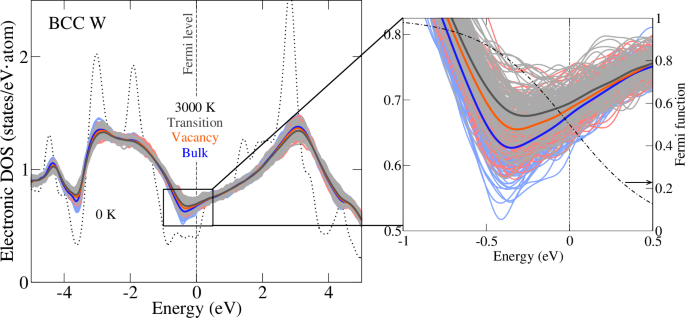
电子影响可以通过对电子态密度 (eDOS) 的分析来理解。图 4显示从分子动力学快照中提取的 3000 K 时的电子态密度。由热振动引起的平滑效应（即，接近费米能级时峰的减少和谷的增加）随着块体到空位到过渡态的顺序而变得更强，正如从平均 eDOS 中观察到的那样（实线（分别为蓝色、红色、黑色）每条均超过 120 张 MD 快照（较浅的背景，具有相似的色调）。尽管单个快照的 eDOS 存在相当大的差异，但平均值的标准误差比不同类型结构（块体、空位和过渡态）之间的差异小大约一个数量级，特别是在山谷和山峰（参见补充图。 4），表明 eDOS 具有良好的收敛性。在高温（电子）下，费米函数（右图所示的点划线）将电子从费米能级以下重新填充到费米能级以上的较高能态。由此产生的空穴和受激电子是电子熵对自由能贡献的根源。一个大的费米能级的 eDOS 促进了许多此类激发，因此意味着很大程度上是负面的电子自由能，详见参考文献。⁵⁰。如图右图放大的山谷区域周围观察到的那样。 4，eDOS 接近费米能级的程度随着块体到空位到过渡态的顺序而增加。因此，空位形成和迁移吉布斯能预计会有更负的自由能贡献，如图所示。 3。

显示了 3000 K 时体结构（蓝色）、空位结构（红色）和过渡态结构（黑色）的平均电子密度。从中获得平均 DOS 的 120 个 MD 快照的相应 DOS 在背景中以相应颜色的较浅版本绘制。右图显示了靠近费米能级的山谷的放大视图。点划线曲线表示 3000 K 时的费米函数。

迁移原子及其邻域的集体运动

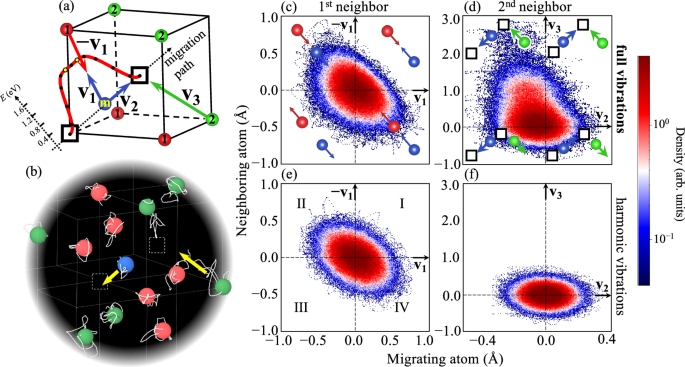
对于空位形成过程，非谐性的物理起源在当地的 Grüneisen 理论中得到了很好的理解²³。这里开发的 TSTI 方法还允许我们访问空位迁移过渡态的完整振动空间。为了了解强非谐性的基本物理原理，我们收集了 3 × 10 的长期分子动力学轨迹⁵步骤（1.5 纳秒）并检查迁移原子相对于其第一和第二邻居的相对运动。几何关系如图所示 5一个。如图所示 5c-f，我们绘制 1 的位移投影^英石(2^ND) 相邻原子到v₁（v₂）相对迁移原子在 上的投影 v₁（v₃）。向量v1_{和 –} v1_{沿着连接迁移原子和 1 的线彼此相对}英石^{邻居原子。}向量v2_和v3_{指向空位中心（【111】方向）。}图 5：迁移原子及其邻近原子的集体运动。一个

英石邻居；^{绿色原子：2}ND^{邻居）处于过渡状态。}红色能量剖面显示计算出的 NEB 最小能量路径，标记有中间图像（黑点）和鞍点（黄点）。乙300 MD 步骤的短时间范围内的实时 MD 轨迹（与每个原子相关的白线）（黄色箭头突出显示集体运动的方向）。c—f迁移原子与其第一（1英石^{列）和第二个（2}ND^{列）邻居考虑全部非和谐相互作用（1}英石^{行）和仅准谐波相互作用（2}ND^排）。轨迹在乙和分布函数c—f对应于 3400 K 和相应晶格常数 3.24 × 时的 MTP 分子动力学。由图可见 

5、全振动（（c）和（d））和谐波近似（（e）和（f））描述了相对运动分布的不同场景。对于与第一个邻居的相互作用，我们观察到由于泡利排斥而导致谐波对称性的破坏，正如之前在体非谐性中发现的那样⁵¹。两个原子朝向彼此的运动在能量上是不利的（在（c）中象限 I 中的分布受到抑制），而彼此远离的运动是有利的（在象限 III 中的分布增加）。完全非简谐势的这一独特特征不能用任何谐波势来描述，因为无论两个原子彼此靠近或远离，后者总是会强制执行相同的能量分布。

对于第二个邻居与迁移原子的相互作用（图1） 5d)，我们同样观察到强烈的不和谐性。分布函数非常偏向正方向v3_向量。这意味着第二个邻居朝向空位的运动在能量上是优选的。实际上，第二个邻居被吸引到了空置的地点。空位附近的原子的这种优先向内振动被报道为空位形成²³。由于鞍点处存在迁移原子，有趣的是，迄今为止尚未报道，2 的这种非和谐向内运动ND^{相邻原子与迁移原子的运动相关：当迁移原子远离空位（朝向另一个空位）时，它特别有利，如图 1 象限 I 和 II 中的非对称分布所示。}一个 5d 并在图 1 所示的实时 MD 轨迹中用黄色箭头突出显示。 5b.这些非谐波特征在谐波分布中完全不存在。请注意，一组原子的这种协调运动可能有利于浅层潜在景观，因为预计会在熔体中扩散⁵²、非晶材料⁵³，甚至用于晶界扩散⁵⁴。

钨的非阿累尼乌斯自扩散

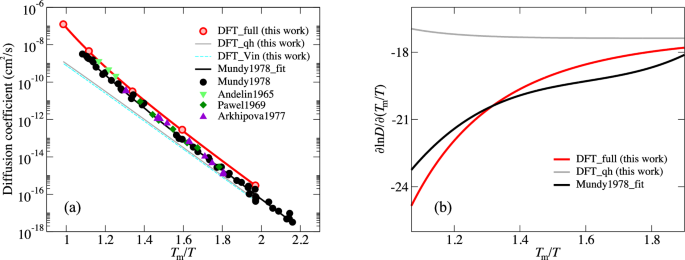
计算的自扩散的阿伦尼乌斯图如图所示。 6a 作为反同源温度的函数，并与最可靠的实验进行比较^12,55,56,57。我们使用DFT-PBE预测熔点为3349 K⁵⁸目前的 DFT 结果和 CRC 手册中的实验熔点 3687 K⁵⁹为实验数据。逆同源温标上的阿伦尼乌斯图补偿了 BCC W 的 DFT (GGA-PBE) 预测熔点和实验熔点之间的显着差异（超过 300 K），如参考文献中所述。⁴⁰。绝对温标上的相应图提供在 补充信息。

一个与 Mundy 等人的实验数据相比，使用所提出的从头算机器学习 TSTI 方法计算的 BCC 钨中的自扩散率阿伦尼乌斯图，在同源温标上考虑了所有有限温度激励（红色圆圈和线）。¹²，安德林等人。⁵⁵，帕维尔等人。⁵⁶和阿尔希波娃等人。⁵⁷。乙阿累尼乌斯图的温度相关斜率比较一个。图 2 揭示了扩散系数的强烈非线性温度依赖性。 

6b.完整的 DFT 结果与实验非常吻合。相反，从（准）调和近似（hTST；包括简化的 Vineyard 公式）导出的扩散率会产生不正确的线性行为。由于目前的 DFT 准调和结果充分考虑了热膨胀效应，因此先前提出用来解释非阿伦尼乌斯行为的晶格膨胀⁶⁰，在高温非阿拉尼乌斯扩散中扮演的角色可忽略不计。我们得出的结论是，钨的非Arrhenius自扩散源自单次单vac的形成和迁移。由于计算基于单个单相化机制，因此完整DFT结果与实验的一致曲率表明，替代性DI-VACANCANCY机制在钨的非Arrhenius扩散中起较小的作用。对Di-VACANCANCH假设进行的详细分析，同样导致了这种机制的排除。 补充信息。我们将计算出的扩散系数的剩余差异归因于实验（图 6A和补充图。 5）到所采用的交换功能和实验不确定性。

TSTI的一般适用性

作为TSTI的关键成分，即动态基质和MTP力的稳定性是独立于系统在其构造中，TSTI方法可以应用于任何晶体结构的金属和合金中的扩散。尽管我们主要关注这项工作，主要是在钨的自扩散上，但TSTI在更复杂的系统（例如五组分高凝集合金（HEAS））中的应用正在途中。之前的研究^61,62已经证明，即使对于这种复杂的多组分系统，MTP在描述振动相位空间方面都是有效且准确的。只有2 3 MeV/Atom的可实现的根平方错误是直接提升成功的基础前提。

为了证明TSTI对具有不同晶体结构以外的其他晶体结构的一般适用性，我们显示了初步的结果 补充信息对于新的六角形封闭式包装（HCP）HEAS，Al₁₅铪₂₅钪₁₀钛₂₅锆₂₅，具有有希望的机械性能⁶³以及在实验和理论中引人入胜的缺陷和扩散特性^64,65,66,67。已经开发了具有2.5 MeV/Atom的RMSE的精确MTP。最终行为良好\（{\ langle {} _ {\ lambda} \）曲线（补充图 9a）和在过渡状态下迁移原子（ZR）的稳定MD轨迹（补充图。 9b）证实TSTI方法的广泛适用性和鲁棒性能。对HEAS中DFT精度扩散的完整模拟研究需要增加计算工作，这是由于额外的化学复杂性。必须进行构型和振动程度中的统计抽样，并且必须进行融合以获得合理的扩散。这样的调查超出了本研究的范围，并且是一个单独项目的重点。

利用定制的机器学习潜力，我们开发了一个有效的依从框架，过渡状态热力学整合（TSTI）方法，以准确计算过渡态的吉布斯能量。到目前为止，固有的动力不稳定性限制了热力学整合的使用。

我们已经应用了提出的框架来预测BCC W的温度依赖性空位迁移和形成Gibbs能量，从而揭示了强烈的Anharmonic原子振动。所得的迁移和形成Gibbs能量表现出明显的非线性温度依赖性。通过对长期分子动力学轨迹的分析，我们将强烈的非谐度与第一个和第二个邻居原子的非对称相对运动相关，相对于过渡状态的迁移原子。预测的依赖温度的自扩散系数清楚地显示了非Arrhenius曲率，并且与在同源温度尺度上的实验数据非常吻合。相比之下，通常应用的准摩尼克近似无法解释观察到的非阿里尼乌斯行为。

开发的框架为探测以前的准确性（包括在整个温度范围内的过渡状态）探测扩散行为的新途径。它使我们能够理解观察到的扩散异常，并解决长期且高度争议的问题。亚稳态和不稳定相的扩散性能具有密度功能理论精度可以计算，这对于（calphad-type）移动性数据库的一致和可靠的开发至关重要，并且没有实验性数据（例如BCC AL或BCC Al或BCC）NI用于评估与基于NI的超合金相关的B2 NIAL阶段的迁移率）。特别是，对于动态不稳定的阶段，由于不稳定性，将TSTI与直接UPS采样相结合的当前计算框架，含空置结构的放松以及轻度弹性带方法变得不可行如果可以在升高温度下在分子动力学中动态稳定它们。一旦获得了已知自由能的适当参考电位，就可以使用TSTI从参考电位到全部振动电位（在本工作中的矩张量（MTP））来获得Anharmonic自由能贡献，然后直接提高采样以实现全密度功能理论的精度。例如，可能的参考是有效的谐波电位或稳定终点的爱因斯坦固体⁶⁸以及从过渡状态的稳定参考元素插值的迁移路径⁶⁰。

随着扩散数据在开发高级材料中的越来越重要，非常需要准确的扩散理论预测。由于引入的方法是一般的，因此可以将其扩展到空位介导的扩散到其他扩散机制的过渡状态吉布斯能量。我们已经表明，它可以应用于复杂的合金系统，例如高渗透合金，其中吉布斯能量从配置自由度扩散也表明了非arrhenius行为⁶⁷。在五组分HCP HCP高渗透合金系统中，在过渡状态下迁移原子的稳定分子动力学轨迹支持TSTI的适用性。引入和经过验证的TSTI方法可以直接在标准的热力学融合代码中实施，因此可以建议在其他应用中进行社区使用和多功能测试，尤其是在扩散控制过程的研究中。作为一个最终目标，可以期望全面的物理信息准确的扩散数据库。

从头开始的自由能量方法用于缺陷

空缺形成和纯属迁移的温度依赖性吉布斯能量表示为

和

在哪里G_大部分,G_真空， 和G_TS是完美散装，空缺和过渡状态超级电池的吉布斯能量，以及氮是完美散装超级电池中的原子数。在给定温度（零压）的平衡体积下，吉布斯能量和赫尔姆霍尔茨能量重合。为了说明各种相关温度依赖性热激发，Helmholtz能量被绝热地分解为²⁶

在哪里乙_0K表示0 K总能量，F^qh和F^啊非相互作用的声子（Quasiharmonicity）的贡献和明确的声子互动（非谐音）。更远，F埃尔指的是电子自由能，并考虑了所考虑的热振动的影响。^{所有自由能贡献对应于平衡体积}V情商（_时间）在温度下时间根据热膨胀。Quasiharmonic自由能F

qh通过应用Bose-Einstein统计数据来填充声子能级，即，即 ^{$$ {f}^{{{{\ rm {qH}}}}}} = {\ sum} _ {i}^{3n} {3n} \ left \ left \ {\ frac {\ hslash {\ hslash {\ hslash {\ omega}}

}+{{{\ rm {k}}}}} _ {{{{\ rm {b}}}}} t \ ln \ left [1- \ exp \ left（ - \ frac {\ frac {\ hslash {\ hslash {

随着普朗克常数减少和声子频率 -_我。有限置换超级电池方法⁶⁹用于提取声音频率，如音频实现⁷⁰。

对于过渡态，等式中语音模式的集成。（15）如常规的谐波过渡态理论（HTST）所述，排除沿反应路径的单个虚构模式²⁷。

明确的无谐自由能F ^啊

热力学积分

明确的无力自由能F^啊，即，可以通过应用热力学整合（用于散装和空置配置）或提议的，可以提取全部振动自由能与准毛电自由能之间的差异过渡状态热力学整合（TSTI；对于过渡态）沿着Quasiharmonic电位之间的预定义的热力学途径，乙^qh，以及全部振动电势，例如，力矩张量电势（MTP）乙^MTP在这项工作中。实际上，热力学路径通常是通过线性插值来建立的，即

在哪里我”是一个耦合参数，值在0到1之间。我”，MD模拟中的原子运动是由任何一个描述的力驱动的乙^qh（我”= 0）或乙^MTP（我”= 1）或两者的线性混合乙_我”（0 < 我”<1）。然后，非谐的自由能读取

在哪里。îF^向上完全DFT准确性可以从直接UPS采样获得⁶²。

直接提升采样

MTP和DFT之间的自由能差可以使用自由能扰动表达以扰动方式计算，如

哪里k_乙是玻尔兹曼常数，乙^DFT和乙^MTP是从MTP轨迹获得的分子动力学快照的DFT和MTP能量。

电子自由能，包括热振动耦合效应

由于与DFT相比具有准确的MTP力（图 2b），也可以应用自由能扰动理论来捕获使用MTP产生的MD快照的DFT之间的自由能差。可以通过将DFT计算中的电子温度设置为相应的分子动力学温度来考虑电子自由能，包括耦合效应³⁶， IE。，

力矩张量电势

潜在形式

为了提高TSTI计算，我们采用了力矩张量电势（MTP）³⁵。MTP利用力矩张量描述符来表征局部原子环境n我（参见补充图 ₂）：$$ m _ {\ mu，\ nu}（n_i）= \ sum \ limits_j f _ {\ mu}（| r_ {ij {ij} |，z_i，z_j）\ underbrace {{{\ boldsymbol {\ boldsymbol {r}}}}}}} _J} \ otimes ... \ otimes {{\ boldSymbol {r}}} _ {ij}} _ {\ nu \ \ {{\ nu \ {{\ mathrm {times}}}}}}，$$

f¼_{封装有关相对原子距离的信息（}£r我j£）和化学类型（_{z我，一个} zj），而角部分_r我j_。。。_r 我j代表惯性的时刻。 径向功能表示为_{$$ {f} _ {\ mu}（| {{{{\ boldsymbol {r}}}}}} _ {ij} |，{z} _ {i}，{z}，{z} _ {j} _ {j}）= {\ sum}_ {k} {c} _ {\ mu，{z} _ {i}，{z} _ {j}}}^{k} {k} {t} {t} _ {k}}}} _ {ij} |

在哪里\（{c} _ {\ mu，{z} _ {i}，{z} _ {j}}}}^{k} {k} \）是适合的径向系数吗？时间_k（£r_我j£）是秩序的Chebyshev多项式k， 和右_切是截止半径（补充图中的红色箭头 2）。在这里，我们使用的截止半径为5.2 - 覆盖了BCC W的1NN，2NN和3NN邻居壳，用于从0 K到3400 K的所有平衡晶格常数，这足以描述本地环境。对于角部分，为了确定电势的基础，必须设置所谓的最大矩水平，\（{{{\ rm {lev}}}}} _ {\ max} \），在参考文献中定义。⁷¹使用的表示法氮g卡氮是价值\（{{{\ rm {lev}}}}} _ {\ max} \）。通常，矩的最大水平越高，MTP模型所具有的基函数数量和拟合参数越大。在这项工作中，高级24G MTP模型（\（{{{\ rm {lev}}}}} _ {\ max} \）= 24）选择了一个单位钨系统的912个拟合参数，以确保描述振动空间的准确性。势能表示为所有当地环境的贡献之和，即乙^MTP=_我V（n_我）=_我±¾_±乙_±（n_我）， 在哪里乙_±表示从张力张量的收缩衍生出的基础功能，并¾_±表示线性拟合参数。

培训数据集和积极学习

用于培训的DFT数据集从NVTMD快照在3600 K和四个不同的晶格常数（3.206ã，3.227，3.227，3.248 - 和3.268到），以确保MTP可以探索和学习足够大的振动空间。

根据参考文献中详细介绍的主动学习计划的迭代方法。⁷¹被用来自动选择要在训练集中添加的新配置。基于D-极端标准，推断级γ可以使用所谓的Maxvol算法为每个新生成的MD快照计算⁷¹。与训练集中的新结构相比，推断级是对新结构的新颖性的量度。从数学的角度来看，如果γ大于统一⁷¹。推断级越高，级别是MTP的外推。在培训过程中，我们使用了选择阈值γ_选择= 1.1，即，通过DFT计算出大于1.1的新构型的能量和力，并添加到训练集中。

主动学习方案始于初始的MTP，该MTP经过200个散装MD结构而训练。在上一步中获得的MTP进行了新的MD运行，从中选择了新的散装结构，空位结构和过渡状态结构并将其添加到训练集中。然后，通过更新的培训集对MTP进行了重新训练。当MD运行期间的新结构在统计学上微不足道时，积极的学习程序就停止了。最终的训练数据库包含806个散装结构，872个空置结构和913个过渡状态结构（总共2591个）。

计算细节

DFT计算

从DFT计算中获得了选择用于训练机器学习势以及上采样快照的能量的配置的总能量和力。GGA-PBE交换相关函数用于所有DFT计算。先前的AB INTIO研究²³与其他功能相比，在依赖温度依赖性空缺形成的吉布斯能量表现出了PBE的出色性能。PBE函数还应用于Ref Ref中的耐火性BCC元素。⁴⁰，并且在同源温度尺度上表明了对熔点的热力学特性的很好的预测。在参考文献中。⁴⁰还计算出空置形成的吉布斯能量，一次在0 K处，然后在一个高温点，表明温度依赖性很强。在最近的另一项研究中⁵⁸，BCC W的熔点是用PBE功能计算的，这可以与同源温度尺度上的实验数据进行比较。因此，PBE功能非常适合我们的本研究，我们的模拟与BCC W的形成和迁移吉布斯能量的全温度依赖性很好地补充了可用的文献。

5d⁴6s²使用了来自VASP电位数据库的价轨道。平面波切割设置为250 eV。使用了基于常规BCC单位细胞的4âââ€4膨胀的超级电池（散装结构的128个原子，空位和过渡状态的127个原子）。一个î - 以中间的和monkhorst-pack⁷²k - 除了单独的准式计算外，所有3âââââ€3的点均使用，其中将9 -9的网格用于收敛。自洽电子环的收敛标准指定为10⁵EV（10⁶EV用于准时计算）。

弹性弹性带计算

过渡状态结构\（\（\ {{{{\ bf {r}}}}}} _ {i}^{{{\ rm {sp}}}}}}} \} \）在给定的体积中是从基于DFT的攀岩图像裸弹性带（NEB）获得的³⁸在VASP中实施的计算，具有11个中间图像。图像之间的弹簧常数设置为5 ev/â…²。当所有力小于0.05 eV/ã时，使用准牛顿算法的NEB离子松弛被停止。所有中间图像的总能量以及两个端点一起使用切向力以准确定位鞍点的输入，将基于力的立方样条插值拟合，如VTST-Scripts所实现⁷³。

热力学积分

在每个温度和体积下利用高度优化的机器学习潜力（时间,V）点，可以使用八个从准时电位到完全振动矩张势的热力学整合（Ti）有效地进行我”值，即0、0.2、0.4、0.6、0.8、0.9、0.95和1，然后是切线拟合。运行所有TI MD模拟，直到达到产生的自由能的标准误差低于0.05 eV/电池。Langevin恒温器的摩擦参数为0.01 fs¹和5 fs的时间步骤。

直接提升采样

对于直接提高采样过程，根据体积和温度，由DFT计算的MTP MD快照数量为360至720。这些数字比散装的一般上取样过程大的数量级以上（20 〜30个快照，精度为1 MeV/Atom）。最终的收敛使我们能够达到低于0.2 MeV/原子的精度。每个原子的这种非常高的精度转化为约20 MeV/缺陷的精度。

作者和单位

1. Institute for Materials Science, University of Stuttgart, D-70569, Stuttgart, Germany

   Xi Zhang & Blazej Grabowski

2. Institute of Materials Physics, University of Münster, 48149, Münster, Germany

   Sergiy V. Divinski

贡献

X.Z.designed and conducted the simulations, S.D.checked the comparison with the experiment, X.Z.and B.G.analyzed the results and wrote the manuscript.所有作者都审阅了手稿。

通讯作者

通讯至张曦。

利益竞争

作者声明没有竞争利益。

同行评审信息

自然通讯thanks the anonymous reviewer(s) for their contribution to the peer review of this work.同行评审文件可用。

开放获取This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.本文中的图像或其他第三方材料包含在文章的创意共享许可证中，除非在材料的信用额度中另有说明。如果文章的创意共享许可中未包含材料，并且您的预期用途不得由法定法规允许或超过允许的用途，则需要直接从版权所有者那里获得许可。要查看此许可证的副本，请访问http://creativecommons.org/licenses/by/4.0/。转载和许可

关于本文