使用巴基斯坦信德省的人工神经网络预测心血管疾病死亡率

心血管疾病（CVD）是一个广泛的术语，涵盖各种心脏和血管疾病。据世界卫生组织 (WHO) 称，它是全球主要死亡原因，每年估计有 1790 万人因此死亡。最常见的 CVD 类型包括冠状动脉疾病、中风、心力衰竭和外周动脉疾病。随着时间的推移，多种因素可能会导致这些病症的发生，包括高血压、高胆固醇、吸烟、糖尿病、肥胖、缺乏运动和心脏病家族史。https://www.who.int）。在信德省，心血管疾病是一个严重的公共卫生问题。年龄、性别、肥胖、高血压、高血糖、高血脂是心血管疾病的主要危险因素。尽管如此，我们对海得拉巴城市和农村地区人口的发生频率和风险因素知之甚少。1]。CVD 的负担的特点是其广泛流行，因为它仍然是全球死亡的主要原因。这包括生命损失和受影响的人员伤亡以及管理和治疗这些疾病的经济负担。此外，早期诊断和治疗对于控制心血管疾病和降低严重并发症的风险至关重要。除了不健康的生活方式选择外，心脏病的其他危险因素包括吸烟、饮酒、高胆固醇、肥胖、高血压和糖尿病。2]。根据世界卫生组织的说法，心血管疾病是一组心脏和血管疾病。2019 年，CVD 导致全球死亡人数估计为 1,790 万人。其中，占全球死亡人数的 32%。根据世界卫生组织关于巴基斯坦心脏病发病率的最新数据，2020年巴基斯坦有240720人死于冠心病，占总死亡人数的16.49%。死亡的强度和比例不断增加，这对巴基斯坦和东南亚的公共卫生构成危险（https://www.who.int/data/gho/data/countries）[3,4]。

CVD 病例建模是一项多学科工作，它利用了各种方法，从流行病学和统计学到尖端的机器学习和人工智能技术。这些模型有助于揭示导致 CVD 的复杂因素网络，包括遗传学、生活方式选择、环境因素和医疗保健干预措施。在这个数据驱动的医疗保健时代，CVD 建模方法处于预测、预防和管理这种普遍且改变生活的疾病的最前沿。它们为疾病趋势、风险因素和干预措施的有效性提供了宝贵的见解。5,6]。文献中已应用多种模型来模拟和预测 CVD 引起的死亡率。采用三种不同的统计模型来预测心脏病，特别是利用支持向量机（SVM）、决策树（DT）和逻辑回归模型（LR）[7]。调查显示，通过应用“C 规则”并采用各种组合，可以提高预测准确性[8]。引入了时间序列模型，提出了一种用于 CHD 预测的新方法，称为组合强化多任务渐进时间序列模型。9]。研究结果表明，深度强化学习（DRL）预训练和多任务处理在 CHD 预测中表现出优越的性能。在另一项研究中，利用五种机器学习模型来预测每日因心血管疾病 (CVD) 入院的情况[10]。在对关键绩效指标进行比较后，很明显，随机森林 (RF) 模型在预测每日 CVD 入院人数方面优于同行。为了进一步增强心脏病的预测，应用了混合时间序列建模方法，结合了支持向量机模型（SVM）和随机森林（RF）[11]。这种混合模型将预测效率显着提高了 88.7%。

此外，ARIMA 模型被用来预测 CVD 患者的死亡率，其在这方面的效率得到了适当的关注。12]。研究人员采用 Lee-Carter 和贝叶斯年龄阶段队列 (BAPC) 模型进行更广泛的死亡率趋势预测，将英格兰的预测延长至 2030 年。13]。在疾病分类和预测的背景下，应用了各种机器学习模型，特别是罗马尼亚的国际疾病分类（ICT）[14]，研究结果强调了模型在此预测任务中的重要性。作者[15] 基于线性和非线性时间序列模型进行了比较分析，使用 6064 个样本量来预测 ICU 住院情况。数据被精心划分为训练集和测试集，最终揭示了高斯朴素贝叶斯和逻辑回归混合模型（GB-+-LR）在预测心脏病患者的总生存期方面表现出优越的性能。研究了基于机器学习和传统逻辑回归预测 CVD 的比较评估[16]。结果表明，机器学习模型的预测比经典方法更准确。作者[17 号] 还在流行病学研究中使用时间序列回归来调查短期关联。据研究，高血压被认为是发生 CVD 的重要危险因素之一。18]。研究 [19]旨在探讨心肌梗死（MI）危险因素之间的关系，并为此应用二元逻辑回归。研究发现，性别、家族史和其他相关变量对于心肌梗死具有统计学意义。风险因素调查[20] 发现在巴基斯坦，多种危险因素在罹患 CVD 方面具有统计学意义。

此外，作者[21] 在 NICVD 上进行了一项关于 CVD 知识的横断面研究。逻辑回归[22] 用于预测慢性病并与机器学习模型进行比较。有关这些研究的更多详细信息，鼓励感兴趣的读者参考相应的引文[23,24]。

ARIMA 和Seasonal-ARIMA 是统计和计量经济学中使用的时间序列预测模型，用于分析和预测时间相关数据的模式。ARIMA 之所以重要，是因为它为时间序列数据建模和预测提供了灵活的框架，使其成为一个有价值的工具。同时，SARIMA 可以对表现出短期波动和长期季节性模式的时间序列数据进行更准确的建模和预测。以 ARIMA 和 SARIMA 为代表的时间序列模型在分析 CVD 发病率数据和进行短期预测方面具有广泛的用途。ARIMA 模型是最著名的时间序列预测模型，已被许多研究人员用来预测具有特征性季节性爆发的传染病。25,26]。

阿尔莫索瓦等人，[27]表明机器学习模型在预测通货膨胀变量方面比现有经典模型具有优越性。然而，研究[28,29]表明 ANNAR 模型在建模和预测 COVID-19 患者死亡方面优于经典方法。同样，文章[30] 提出了基于 ANNAR 的流感事件集成模型。研究发现，基于 NNAR 的模型的准确度误差最低。

中国山东省的一项研究利用 SARIMA 模型恰当地捕捉中风发病率数据的季节性和趋势模式，展示了该模型有效表征此类时间动态的能力。31]。鉴于 ARIMA 模型的缺点，人们越来越关注使用 ANN 模型进行流行病学时间序列预测[32] 因为这些模型解释了数据中的非线性。机器学习模型，包括人工神经网络 (ANN) 和支持向量机 (SVM)，已成为 CVD 预测的重要工具。与传统的时间序列模型相比，在中国上海实施的基于 N 的方法证明了中风发病率具有更高的预测准确性。33]。

本研究旨在通过比较传统的线性和非线性机器学习模型，使用各种随机时间序列模型来建模和预测 CVD 的年死亡率。本文结构如下：首先，我们回顾了 CVD 预测的相关文献综述和先前的工作。此外，我们提供了与数据描述和方法相关的详细信息，然后概述了结果及其解释。最后，我们对未来的研究方向提出政策建议。

本研究的数据集是从巴基斯坦信德省纳瓦布沙赫地区的民用医院收集的。它包括 1999 年至 2021 年间发生的 CVD 相关死亡的实际病例。这个广泛的集合提供了可靠的时间序列数据集，涵盖了二十多年来 CVD 死亡率的趋势和模式，其中包含年度数据。该数据集的广泛时间范围使得对心血管疾病相关死亡率随多种因素的变化进行彻底检查成为可能，这些因素包括医疗基础设施的变化、公共卫生运动、生活方式的调整和该地区的社会经济进步。通过利用这一丰富的数据集，学者们可以对心血管疾病的流行病学有深入的了解，查明可能的危险因素，并制定针对性的治疗措施，以减轻信德省心血管疾病的患病率。该数据集没有任何缺失值，并用于实际观察。此外，该数据集还获得了医院管理部门的伦理批准。

统计分析

这些数据是从 1999 年至 2021 年信德省 Nawabshah 巴基斯坦民事医院收集的，重点关注受 CVD 影响的人数。为了理解这些随时间变化的数据，采用了一种称为“时间序列分析”的特定方法。分析过程涉及几个阶段。最初，将对数据进行描述性分析，以确定模式和基本特征。这为后续阶段奠定了基础。此后，将通过创建时间序列图来可视化数据，从而能够观察多年来 CVD 死亡的趋势和变化。这些视觉表示有助于识别季节性和异常等模式。将应用各种时间序列模型来做出有意义的预测和预报，每种模型都有其独特的方法。这些模型包括简单的“朴素”模型、更复杂的“简单指数平滑 (SES)”方法、“Holt 线性指数平滑”和高度先进的 ANNAR 模型。”这些模型允许探索数据、分析模式。下面给出了数据处理的流程图。

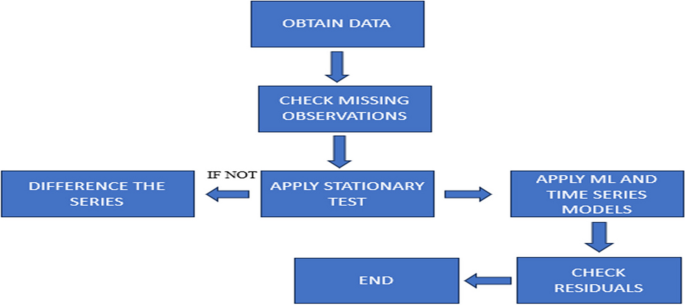
数据说明

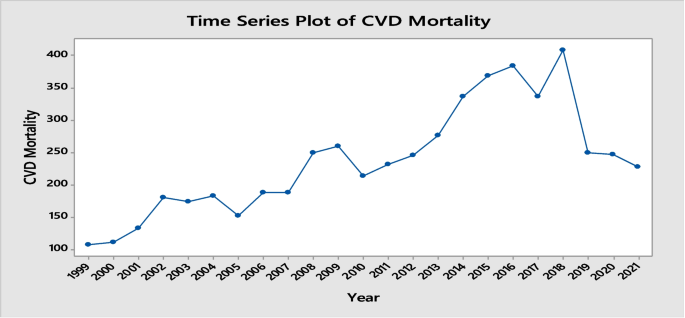
使用一段时间内收集的数据点的图形表示构建时间序列图，然后用于分析和可视化数据随时间的变化。图 1显示心血管疾病死亡的年度时间序列的直观显示。检查图 1 中的时间序列图。 1表明有增加和减少的趋势。

每年CVD死亡病例时间序列

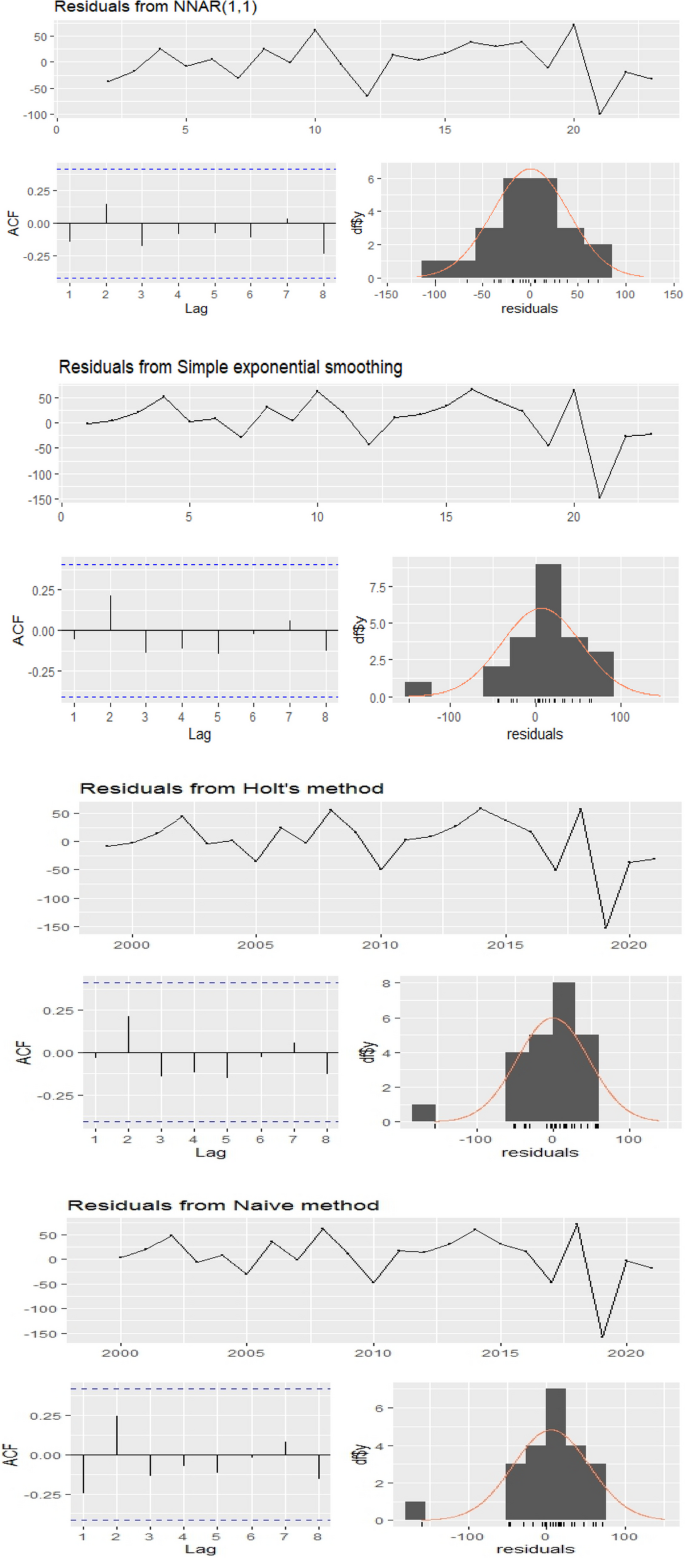
应用这些模型的主要重点是捕获该系列的数据生成过程。经典时间序列和机器学习模型都侧重于短期预测，然后通过指标测试进行比较。数据分为 80% 的训练（1999 年至 2016 年）和 20%（2017 年至 2021 年）的测试进行验证。汇总统计数据如表所示 1据观察，1999年信德省CVD死亡病例最多为107例，由于多种因素，这一数字持续上升，直到2018年死亡人数上升至408例。平均死亡人数为 236 人，中位数为 231 人。图 3说明了残差诊断图，它在时间序列分析中发挥着至关重要的作用，因为它们有助于评估时间序列模型的充分性。时间序列模型中的残差表示观测值与模型生成的预测值之间的差异。这些图用于直观地评估残差是否符合某些假设：正态分布、同方差性（恒定方差）和独立性（缺乏自相关）。残差直方图用于验证残差的正态分布。此外，R 函数 checkresiduals() 用于执行这些诊断检查，生成时间图、ACF 图、残差直方图和正态曲线。

在时间序列分析和人工智能领域，在使用小样本集时必须更加谨慎，以确保稳健性并防止过度拟合。下面提到的方法强调了它们的用途和稳健性。

朴素的方法

在时间序列分析中，朴素方法是最简单的预测方法，其中预测时间序列中的下一个值等于当前值。它可以用以下等式表示：

在哪里\(\宽帽 y(t+1)\)表示下一个时间段的预测值，并且\(y(t)\)表示当前时间段的实际值。朴素方法假设时间序列是平稳的，并且数据中没有趋势或季节性模式。它是评估更先进的预测模型性能的有用基准。Naïve 方法对数据做出最少的假设，并且由于其简单性而不太可能过度拟合 [34,35]。

Holt-winter 指数平滑法

Holt-Winters 预测也称为三重指数平滑，是一种流行的时间序列预测方法，它使用指数平滑来捕获数据中的趋势和季节性。该方法可以有效处理小样本量，但需要仔细调整参数以避免过度拟合[36]。该方法涉及使用三个平滑方程（一个用于水平、一个用于趋势、一个用于季节性）来生成预测。

方程为：

在哪里：\({Y}_{t}\)= 某时刻的实际值\(t\),\({L}_{t}\)= 时间 t 时的电平，\({T}_{t}\)=当时的趋势\(t, {S}_{t}\)= 时间的季节性分量\(t\),\（米\）= 一年中的季节数\（\阿尔法\）,\(\测试版\)， 和\(\伽玛\)是介于 0 和 1 之间的平滑参数，它们控制应用于每个组件的平滑量。在预测方程中，\({F}_{t}\)表示时期 t 的预测，k 是滞后参数或时移，即提前多少个时期进行预测[37]。

通过估计平滑参数并应用这些方程，可以生成未来时间段的 Holt-Winters 预测。

人工神经网络自回归 (ANNAR) 模型

神经网络模型是一种受人脑结构和功能启发的机器学习模型。它们旨在识别数据模式并根据该数据做出预测或决策。神经网络由互连的节点层组成，称为人工神经元，其灵感来自于人脑神经元的结构。每个神经元接收来自其他神经元的输入，处理该输入，并将结果传递给下一层中的其他神经元。

传统的时间序列模型，例如指数平滑或 ARIMA，假设数据具有线性连接。尽管如此，现实世界中的许多时间序列都显示出复杂的非线性模式。ANNAR 模型由于其非线性激活函数而擅长捕获这些复杂的相互作用[38]。ANNAR 模型的适应性非常强，并且具有多种函数近似值。凭借足够的数据和处理能力，他们可以凭借其通用近似能力对任何底层过程进行建模。ANNAR 模型可以学习和识别数据中的模式，而无需明确指定模型形式 [39]。

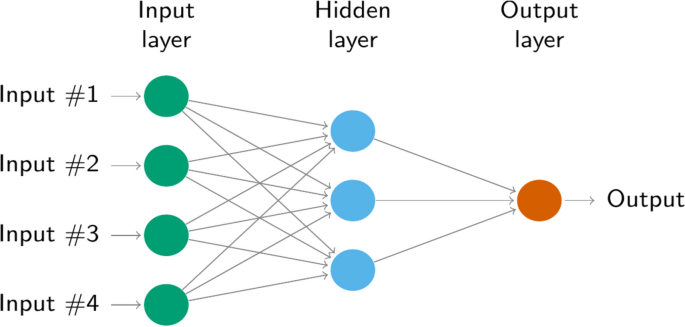
神经网络模型已用于多种应用，例如图像和语音识别、自然语言处理和游戏等。ANNAR 模型已用于预测疾病爆发、患者入院和其他健康指标。它们在处理复杂、多因素数据方面的有效性使它们适合这些应用程序[40,41]。它们是解决复杂问题的强大工具，并在许多任务上取得了最先进的性能[42,43]。这种网络方法允许对任何线性和非线性现象进行建模。神经网络自回归模型是一种基于分层组织的简单神经元结构的模型。这些神经网络进一步分为两类。第一类由最简单的神经网络组成，第二类是复杂的神经网络。简单的神经网络不涉及隐藏层，而复杂的网络则使用多个隐藏层。在这些神经网络中，使用不同的方法来拟合数据。拟合数据最常用的过程是前馈方法。前馈方法的图形如图所示。 2。前馈网络的结构由三部分组成，即用于处理观测值的输入层、用于对这些观测值进行加权的隐藏层以及作为结果网关的输出层。隐藏层负责根据合适的权重年龄链接到数学函数的处理。神经网络自回归的数学方程可以写为：

具有四个输入的 ANNAR 模型，一个隐藏层，具有三个隐藏神经元

在等式中 1变量\({Y}_{i}\)代表使用 sigmoid 函数的隐藏层算法。sigmoid 函数在方程中给出。 7。这里\({W}_{i,j}\)表示与 Y 向量中第 j 个元素的向量 W 中第 i 个元素相关的权重或系数

前馈方法的图形如图所示。 2。

简单指数平滑法

简单指数平滑 (SES) 是一种用于预测时间序列数据的技术。该方法通常适用于任何时间序列的预测。当时间序列数据没有季节性或趋势时，假定该方法最适合。该方法假设连续时间序列观测值的加权过程，因为它随着时间的推移以指数递减的形式分配权重。简单指数平滑的数学公式可以写为[44]。

化简后的方程 8结果

这里的

\({\text{s}}_{\text{t}}=\)当前观察值的平滑统计量或加权平均值\({x}_{t}\)

\({\text{x}}_{\text{t}}\)= 当前时间段。

检测指标

时间序列分析中最重要的任务是评估和选择合适的模型。这是因为研究人员假设所选模型比其他模型更有效。应用合适的预测模型存在标准，其中一些标准如下[45]。

在哪里\({e}_{t}\)代表每年死亡病例的误差项，\({Y}_{t}\)代表在某个时间点观察到的时间序列\(t\)。根据这些标准，我们选择产生最少数字的模型。

该研究从考虑建模样本的数量开始。经确定，大于 50 的样本量对于有效捕获时间序列数据的统计特性是最佳的。当样本量较小时，ARIMA 模型的参数可能会变得更加不准确，从而导致预测不可靠。在这种情况下，简单指数平滑、朴素模型和 Holt-Winter 模型等替代方法可能更合适。46,47]。简单指数平滑对于预测时间序列数据特别有用，尤其是当样本量较小时。这种方法涉及计算过去观测值的加权平均值，随着观测值变老，权重逐渐呈指数下降。为了验证模型，数据被分为 80% 的训练集和 20% 的测试集。

从表中可以看出 2，在训练 80% 的数据时，ANNAR 模型显示所有 KPI 的最低值。由于观测值很少，而且其余 20% 的数量也很少，因此我们将把其余技术应用于完整的数据集。当样本量较小时可以应用神经网络。在机器学习中，神经网络可以应用于不同大小的数据集，范围从几个数据点到数百万个数据点。数据集的大小并不决定神经网络的适用性，而是决定你试图解决的问题的复杂性和神经网络的架构[48,49]。

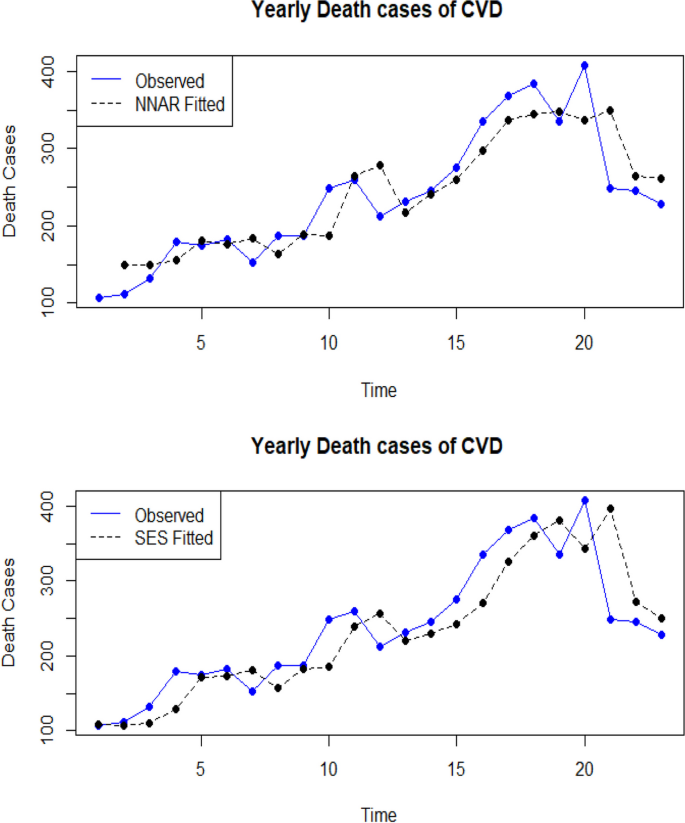
表中的结果 3结果表明，神经网络自回归模型（ANNAR）在完整数据集的测试中优于所有候选模型。死亡案例的均方根误差为 38.86，平均绝对误差为 13.08，这表明 ANNAR 相对于所有其他选定模型具有主导地位。Naïve 模型显示 KPI 的最大值为 MSE ≤= 2304、RMSE ≤= 48、MAE ≤= 33.86 和 MAPE ≤= 13.86，其次是SES 方法显示 MSE 2124.29，RMSE≤=≤46.09，MAE≤=≤33.85，MAPE≤=≤13.22。ANNAR 显示了所有应用的候选模型中 KPI 的最低值，并被证明是信德省 CVD 死亡病例建模和预测的性能更好的方法。此外，我们转换了表 2转化为视觉形式，以便使用基于探索性统计的残差分析更好地理解。死亡系列的残差图进一步显示了 CVD 死亡病例的拟合值与观测值。

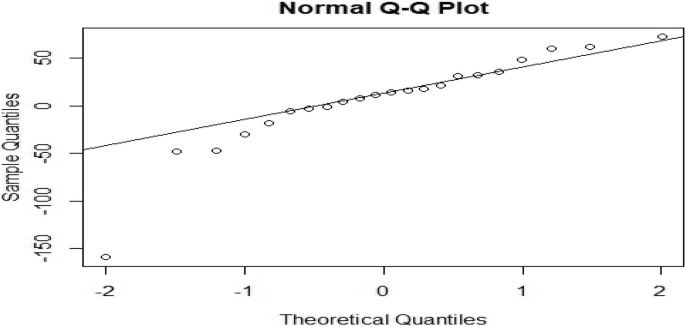
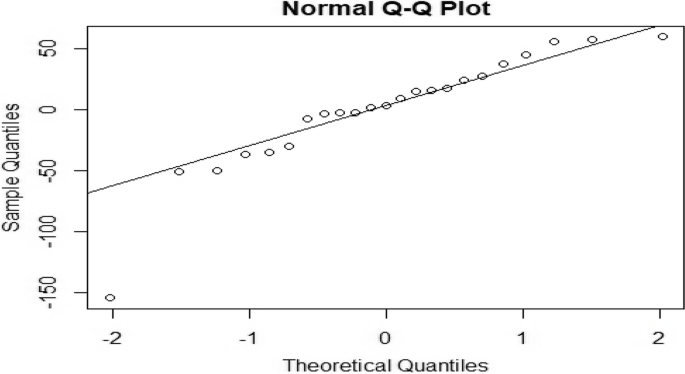
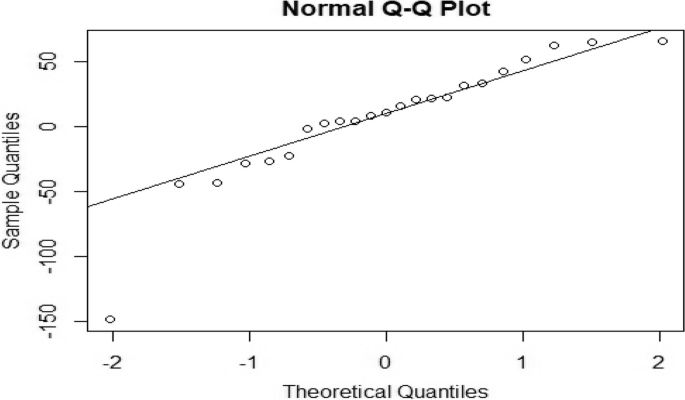
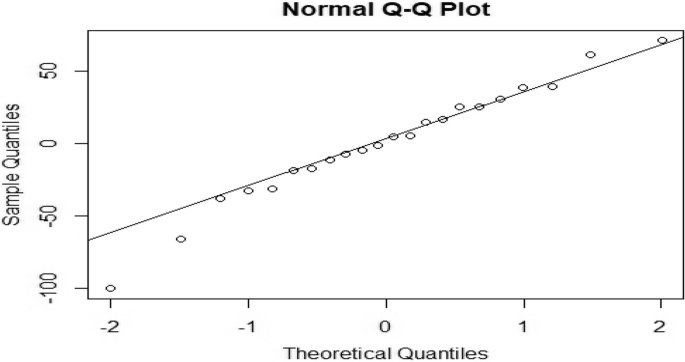
还进行了 Ljung-Box 检验，其中零假设假设残差项之间不存在自相关，表明缺乏模型拟合。残差的诊断检查得出的结论是，所选的 ANNAR 模型表现出令人满意的拟合，残差之间不存在任何自相关性 [47]。图 3呈现诊断结果，包括 ACF 图和残差与正态曲线重叠的图，证明残差的正态性。在正态分布情况下，直方图应显示钟形分布，类似于密度图。值得注意的是，与其他候选模型相比，使用 ANNAR 方法拟合的直方图与残差数据吻合得很好 [50]。此外，ANNAR 模型生成的残差的滞后值落在可接受的概率范围内。为了进一步说明观测值和拟合观测值之间的接近程度，我们绘制了一个图来描述该系列的观测值与拟合值。图 4显示通过神经网络自回归方法与观察到的偏差较小，这表明该模型最适合该系列。然后使用表中给出的预测值来进行下一个五年的预测 4（95% 置信区间）。此外，QQ 范数图在附录中给出。

ANNAR、SES、Holt 和 Naïve CVD 死亡病例的残留诊断

使用 ANNAR 和 SES 观察到的 CVD 与拟合图

近年来，一种称为人工神经网络自回归（ANNAR）的模型已经变得相当强大[51,52]。它擅长理解数据中复杂的、非直接的联系。ANNAR 在各种情况下都有成功的记录，例如预测疾病爆发和评估药物的有效性，这使其受到研究人员的欢迎。53,54,55]。在这项研究中，这项工作使用传统的方法来分析时间序列数据，并使用更现代的机器学习技术来处理小样本。关于长期心血管疾病病例的预测，ANNAR 模型优于其他技术[56,57,58]。此外，该技术可以扩展到趋势分析和其他基于非线性方法的机器学习模型。ANNAR 模型性能的提高可能是由于其强大的训练和优化策略以及准确捕获和预测数据中看到的时间依赖性和复杂的非线性交互的能力所致。59,60,61]。对于各种时间序列预测任务，其多功能性、适应性和复杂的特征处理使其非常适合[62,63,64]。

鉴于结果，建议采取预防措施来减轻信德省CVD的负担，包括促进健康的饮食，增加体育锻炼和减少烟草使用。筛查和早期检测计划还可以帮助诊断和管理CVD，降低并发症的风险和改善结果。信德省的个人需要通过做出健康的生活方式选择并在需要时寻求医疗服务来积极地在管理心脏健康方面。

研究的意义

本研究的重点是通过常规和非线性时间序列模型安纳尔（Annar）模拟巴基斯坦信德省的CVD死亡病例。结果表明，与常规方法相比，这项研究中提出的Annar模型表现出色。这项研究本质上是独一无二的，因为在信德省巴基斯坦省的CVD死亡案件中没有进行此类研究。这项研究可以帮助确定需要更多关注和资源的高风险地区和人群。这些信息可用于优先考虑针对这些人群的预防和治疗策略的资源分配。对CVD死亡案件进行建模可以帮助估计该地区疾病的经济影响以及不同干预措施的成本效益。

根据上述建议，可以在政府层面以及省级采取以下政策措施。

1. 1.

   鼓励健康的生活方式选择：预防CVD的最佳方法之一是采用健康的生活方式，其中包括定期运动，健康的饮食习惯，戒烟和减少酒精消耗。政府可以发起公众的意识运动，以促进健康的生活。

2. 2.

   提供预防保健的机会：早期检测和治疗CVD可以显着降低死亡率。因此，至关重要的是提供预防保健，例如定期检查，血压和胆固醇筛查以及其他诊断测试。

3. 3.

   提高医疗服务的质量：需要改善巴基斯坦的医疗机构，应提高护理质量。政府可以投资医疗基础设施，为医院配备现代技术，并培训医护人员提供更好的护理。

4. 4.

   对不健康产品的税收增加：不健康产品的税（例如烟草和含糖饮料）可以减少其消费并促进更健康的选择。

5. 5.

   提供可负担得起的健康食品的机会：政府可以鼓励健康食品的生产和消费，例如水果，蔬菜和全谷物，并使它们对普通人群更加负担得起。

这些政策可以大大减少巴基斯坦的CVD死亡人数。但是，实施这些政策需要政府，医疗保健提供者和公众之间的持续努力和合作。

心血管疾病是人类死亡的主要原因之一。这项工作旨在预测信德省一名巴基斯坦城纳瓦布沙的年度CVD患者。根据调查结果，信德省急需集中的公共卫生计划，以增加公共对CVD风险因素的了解，例如烟草使用，身体不活跃和不健康的饮食。为了获得最大的效果，可以将教育活动定制为针对特定群体。在建模疾病中，没有一种方法比其他所有方法都更好。方法的选择取决于要解决的问题的特定要求以及数据的可用性。过去通常使用了指数模型，例如简单的指数增长模型，用于建模疾病的传播。这些模型实施相对简单，但是在捕获复杂的疾病动态方面存在局限性。诸如Annar之类的神经网络模型由于能够捕获数据中复杂的非线性关系的能力，因此近年来已获得流行。安纳尔已应用于一系列疾病建模问题，包括预测疾病暴发和药物疗效。这项工作应用了不同的时间序列方法，一种基于经典时间序列方法，第二种方法基于机器学习技术。结果发现，安纳尔在长期预测期内表现优于表现。

未来的研究可以集中于比较Annar和传统时间序列方法之外的更广泛的建模方法。确定Nawabshah预测CVD死亡率的最佳策略，可能涉及使用其他机器学习模型，例如随机森林，支持向量机（SVM）和集合方法。

化学气相沉积：

心血管疾病

安纳尔：

人工神经网络自动回归

社会经济地位：

指数平滑

阿里玛：

自动回归综合移动平均

支持向量机：

支持向量机

RMSE：

根平方偏差错误

梅：

平均绝对误差

Mape：

平均绝对百分比误差

作者和单位

1. 巴基斯坦信德省海得拉巴70060的Govt学位学院Tangojam

   Moiz Qureshi

2. IBN-E-SINA医科大学Mirpurkhas，信德省，巴基斯坦

   Khushboo Ishaq

3. 巴哈瓦尔布尔伊斯兰伊斯兰大学计算学院统计系

   穆罕默德·丹尼亚尔（Muhammad Daniyal）

4. 巴基斯坦伊斯兰堡45320 Quaid-i-Azam大学统计系

   Moiz Qureshi＆hasnain iftikhar

5. 国王沙特大学工商管理学院财政部Box 71115，利雅得，11587，沙特阿拉伯

   Mohd Ziaur Rehman

6. Al-Barkaat管理研究所，Aligarh 202122，A。P. J. Abdul Kalam技术大学，勒克瑙226010，印度

   HasnainIftikharâ＆s。A。Atif Salar

贡献

所有作者（Moiz Qureshi，Khushboo Ishaq，Muhammad Daniyal，Hasnain Iftikhar，Mohd Ziaur Rehman和S. A. Atif Salar）阅读并批准了最终手稿。他们也同样为这项研究做出了贡献，批准了其主张，并同意为作者。

通讯作者

通讯至Hasnain Iftikhar。

道德批准并同意参与

这项研究已获得信德省地区办事处伦理审查委员会的批准，并获得了32E/4/2021号批准。

同意发表

作者没有声明本文的利益冲突。

利益竞争

作者声明没有竞争利益。

出版商的注释

施普林格·自然对于已出版的地图和机构隶属关系中的管辖权主张保持中立。

图5

,

图6HOLTS方法的QQ NORM图

,

图7SES方法的QQ NORM图

和

图8QQ Norm Plot的Annar方法

权利和权限

开放获取

链接到知识共享许可证，并指出是否进行了更改。本文中的图像或其他第三方材料包含在文章的知识共享许可中，除非材料的出处中另有说明。如果文章的知识共享许可中未包含材料，并且您的预期用途不受法律法规允许或超出了允许的用途，则您需要直接获得版权所有者的许可。要查看此许可证的副本，请访问http://creativecommons.org/licenses/by/4.0/。转载和许可

关于本文