粗粒网络通过统计物理和机器学习流动

复杂网络代表了几种天然和人工复合系统的结构¹，该表现出无处不在的特性，例如异质连通性²，有效的信息传输³，中尺度⁴和分层^{5，，，，6}组织。此外，考虑多重性和相互依赖性，可以使用其他信息来丰富这些模型^{7，，，，8，，，，9，，，，10，，，，11}，高阶行为和机制^{12，，，，13，，，，14，，，，15，，，，16}。网络建模和分析的丰富性为跨基因调控范围^{17，，，，18}和蛋白质相互作用¹⁹分子生物学，大脑网络的网络^{20，，，，21}在神经科学中，交通网络²²在城市规划中，到社交网络^{23，，，，24}在社会科学中。

此外，网络科学已被用来研究网络内的信息流，从大脑区域之间传播的电信号和在社交系统之间传播的病原体到航空网络中的航班以及在社交媒体上共享的信息。为了实现这一目标，通常利用了一个动态过程，该过程控制组件之间的短期流量^{25，，，，26，，，，27，，，，28，，，，29，，，，30，，，，31，，，，32，，，，33，，，，34，，，，35，，，，36，，，，37，，，，38，，，，39}。然而，由于计算复杂性和角色和功能的组成部分的冗余，许多现实世界系统的巨大性构成了挑战，因此对复杂系统的运作有了清晰的了解。因此，有趣的可能性是通过将保留流量的冗余特征或角色的分组和粗粒节点进行分组和粗粒节点来搜索网络的适当压缩。

网络重归其化方法的重点是在保留其核心属性的同时压缩网络的大小。已经提出了几种开创性方法来粗粒成分。Song等。⁴⁰将框覆盖方法的概念带入了网络重新归一化领域⁴¹，随后的作品主要集中于提高其效率^{42，，，，43，，，，44}。通常，这些方法将网络视为旋转系统⁴⁵并研究普遍课程⁴⁶和分形特性⁴⁷。作为另一个例子，在未加权图上的几何重归其化⁴⁸和加权图⁴⁹将网络结构嵌入二维双曲空间中，根据节点的角度相似性将节点分组，并将它们合并到宏网络中：在该空间中，它们可以揭示现实世界网络的多尺度组织。本着同样的精神，通过网络动力学引起的有效几何形状已被用来揭示尺度和分形特性⁵⁰。例如，光谱粗晶片⁵¹专注于网络顶部的动态，并尝试在结构压缩过程中保留网络的大规模随机行走行为。最近，一种基于拉普拉斯重归于的方法⁵²基于网络顶部的扩散动力学提出，对应于网络结构中自由场理论的重新归一化。该方法通过保留慢速扩散模式，将RG的边界推向了结构异质性。但是，这些重新规定方法均未旨在在所有网络类型的所有传播量表上同时保留信息动力学的宏观特征。

类似于拉普拉斯（Laplacian）重新归一化组，我们利用网络密度矩阵³³描述系统中的信息动态⁵³。从密度矩阵中，我们得出了典型的宏观指标，例如网络熵和自由能，它们分别量化了扩散途径的多样性^{53，，，，54，，，，55}以及信号在系统中传播的速度^{55，，，，56}。我们表明，此类措施可以从网络分区功能得出z _-，如平衡热力学。从这个理论的基础上，我们推断出一种粗粒，可以保留在传播量表上的分区函数的形状 -，保留信息流的宏观指标。因此，我们旨在达到与完整分区功能概况最小偏差的粗粒。

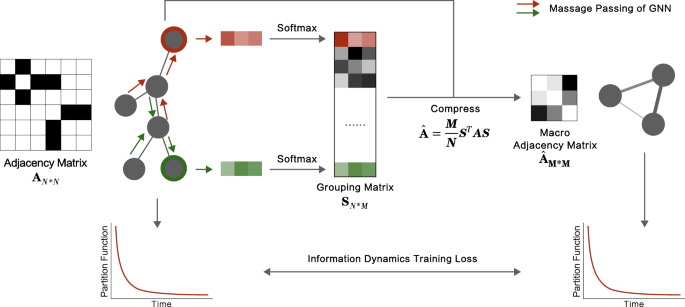
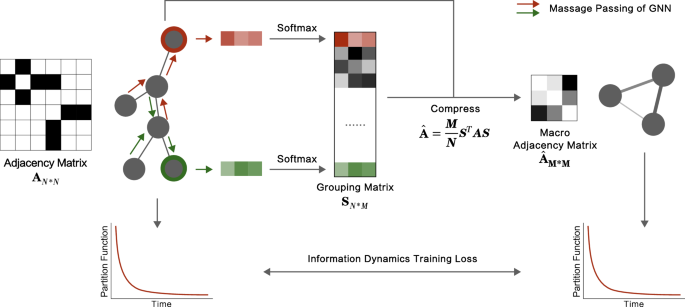
我们绕过为通用复杂网络找到分析封闭解决方案的挑战。避免简化实践兴趣的假设和案例，我们利用基于图表的机器学习的最新进展来开发网络流动压缩模型（NFC模型）的框架，如图所示。 1。从技术上讲，我们使用图形神经网络^{57，，，，58}处理和汇总节点的本地特征，例如连接数（度），并达到它们的高级表示。在表示空间中，它标识了在信息流中扮演冗余角色的节点组的组，这些节点不会大大改变流动，并粗糙晶粒以达到合适的压缩，从而最大程度地减少了分区函数偏差。虽然大多数粗颗粒方法通过将节点与相似的局部结构分组来定义和识别超节点，但它们的相似性概念通常是预定义的^{48，，，，49}。相比之下，我们的方法利用机器学习模型自动学习可用于压缩网络的重要相似性特征，同时保留宏观流动属性。例如，在BA网络中，轮毂节点被合在一起，而叶节结合在一起。在现实世界中的科学家合作网络中，即使与彼此之间的合作没有（连接）合作，他们的合作数量最多的科学家也被划分为一个小组。实验结果在随后的部分中结果表明，即使在合成和经验系统中，我们的方法也可以保留信息流。在后续部分中对模型的可解释性的分析表明，该策略是合理的：它保留了在信息扩散过程中局部结构的功能，同时减少了冗余结构的数量。

GNN的消息通话机制收集邻居的信息，为每个节点创建一个向量表示。SoftMax方法标准化了导致节点组的向量。我们在这里使用的节点功能包括学位 -_d，学位\（{{{{{\ Mathcal {x}}}}}}}}^{2} \）---即给予\ \（{{{{\ Mathcal {x}}}}}}}} _ {i}^{2} = {（e [d] - {\ sigma} _ {d}）}\）其中d是相邻节点的程度---，聚类系数和核心数。在这种情况下，为简单性考虑了3组，在组矩阵中表示s。两者都使用s和原始的邻接矩阵一个，我们进行的压缩操作表示为：\（\ hat {{{{{\ bf {a}}}}}}}} = \ frac {m} {n} {n} {{{{{\ bf {s}}}}}}}}}}}}}}}}^{}}}}} {{{{\ bf {s}}}}} \）\）。在此操作中，\（\ hat {{{{{\ bf {a}}}}}}} \）代表宏网络的邻接矩阵，而m和n分别象征宏和微网络中的节点数量。宏网络的归一化分区函数与原始网络的偏差用作监督GNN的损耗函数。

我们的工作实现了最终与网络重新归一化组方法不同的目的。实际上，这些方法旨在发现系统的缩放行为。例如，重新归一化组方法在压缩网络（例如无标度网络的程度分布）时会保留特定的拓扑特性。但是，在其他情况下，例如，在具有一个或多个特征拓扑尺度的网络中，这些方法有望在压缩时捕获包括流量在内的网络属性的变化。相比之下，无论拓扑的特定特征如何，我们的方法都试图找到一种保留流量特性的粗粒。因此，当比较不同的网络家族时，预计它在保留流程方面将胜过其他人。我们通过图中证明的一系列数值实验确认了这一期望。 2。

适用于两个代表性随机块模型（SBM）网络的压缩过程的视觉表示（混合参数¼分别为0.029和0.127）和Barabasi-Albert（BA）网络（每个节点的链接数量m1和2）。第二行可视化被压缩到35个节点的宏网络的结构。第三行显示在不同大小的压缩之前和之后分区函数中的平均绝对误差。我们在5到200之间的对数空间中均匀地选择了10种不同的尺寸。最后一行在将网络压缩为35个节点时，显示了不同方法的分区函数曲线的平均绝对误差。

最后，我们在大量的现实网络上训练图形神经网络，从而使对以前从未见过的数据集有所概括。我们表明，这导致了来自各个领域的网络之间的快速和高效的压缩。

信息流的宏观指标

让g成为n节点和£e£连接分别。连接通常由邻接矩阵编码一个， 在哪里一个_我j如果节点是= 1我和j已连接，并且一个我_{j=â0否则。}对于加权网络，值一个_我j可以是非二进制的。组件之间的信息交换是通过连接发生的。

我们专注于扩散是代理信息流的最简单，最通用的过程之一⁵⁹由图形拉普拉斯矩阵支配l= d -  一个， 在哪里d是对角线矩阵，有d我我= _{k我是节点的连通性我}。因此，我们编写扩散方程及其解决方案：_{$$ {\ partial} _ {\ tau} {\ psi} _ {\ tau} = - {{{{\ bf {l}}}}}}} {\ psi} _ {\ psi} _ {\ tau}}{\ tau} = {e}^{ - \ tau {{{\ bf {l}}}}}}}}}} {\ psi} _ {0}，$$（1）在哪里

是一个浓度向量，描述了在节点上的数量分布和e _-l提供时间进化运营商，并^{\（{\ left。从节点给出流j}到我后 -时间步骤。网络密度矩阵可以定义为$$ {{{{\ boldsymbol {\ rho}}}}}}}} _ {\ tau} = \ frac {{e}_ {\ tau}}，$$（2）在哪里

\ \（{z} _ {\ tau} = {{{{\ rm {tr}}}}}}} \，（{e}^{ - \ tau {{{\ bf {\ bf {l}}}}}}}}}}}}）\）\）\）\）\）\）\）\）\）

）描述一个指导系统中信息流的运算符（Laplacian矩阵的特征向量的外生产）的叠加53，，，，60，应用范围从健康和疾病状态的分类不等39^{，，，，61和鲁棒性分析}62，，，，^{63减少多层网络的维度56}和重新归一化组^{52。更重要的是，网络von Neumann熵由}\ \（{{{{{\ Mathcal {s}}}}}}}} _ {\ tau} = - {{{{\ rm {tr}}}}}} \，（{{{{{{{^{_ {\ tau} \ log {{{{\ boldsymbol {\ rho}}}}}}}} _ {\ tau}）\）\）}已经研究了该系统对扰动的多样性的衡量标准⁵³，，，，

54，以及网络自由能，\（{f} _ {\ tau} = - \ log {z} _ {\ tau}/\ tau \）^{，以衡量节点之间的信号传输的速度55，，，，56}。由于网络密度矩阵是Gibbsian（等式（2^{））和网络内部自由能可以定义为\（{\ tau}）\）}，我们可以根据网络和内部能量编写网络，并以

z -及其衍生物：$$ {f} _ {\ tau} = - \！\ log {z} _ {\ tau}/\ tau $$（3）$$ {u} _ {\ tau} = - \！{\ partial} _ {\ tau} \ log {z} _ {\ tau} $$_（4）$$ {s} _ {\ tau} = \ tau（{u} _ {\ tau} - {f} _ {\ tau}），$$

n\（{n}^{{\ prime}} \）\）_{，导致新的拉普拉斯人}\（（（{l}^{{\ prime}}）\）\）和新的分区功能 \（（（{z}^{{\ prime}}）\）\）。在这里，我们旨在达到以下的压缩：$$ z = \ gamma {z}^{{\ prime}}，$$（6）不管

实际上，如果两个网络具有不同的尺寸，则乘数的唯一有效值是\（\ gamma = n/{n}^{{\ prime}}} \）。

支持这一说法的一个简单论点是在 -= 0可以证明z= n和\（{z}^{{\ prime}} = {n}^{{\ prime}}} \），无论网络拓扑如何。因此，唯一未被反对示例拒绝的解决方案 -=â0，给出分区函数的最大值，为\（\ gamma = n/{n}^{{\ prime}}} \）。如果\（\ gamma = n/{n}^{{\ prime}}} \）和n和\（{n}^{{\ prime}} \）\）作为原始系统和还原系统的尺寸，这些转换可以解释为尺寸调整。

我们表明，这种压缩同时保留了尺寸调整后的其他重要功能，例如熵和自由能。例如，系统的熵具有最大\（s = \ log n \）在 -= 0，可以将其转换为压缩熵，并通过因子的减法而变为\（\ log \ gamma \）作为尺寸调整\（s \ to s- \ log \ gamma \）。同样，自由能\（f = - \ log z/\ tau \），所需的调整尺寸读取\（ - \ log z/\ tau \ to - \ log z/\ tau+\ log \ gamma/\ tau \）。

我们之前讨论的分区函数转换（z -  Î³z，因此\（{z}^{{\ prime}} = z/\ gamma \）），自动保证这两个转换：

同样，由于粗粒系统的von Neumann熵由

内部能量的转化可以作为：

在下一节中，我们使用机器学习来查找通过近似来复制原始熵和自由能曲线的压缩。\（{z}^{{\ prime}} = z/\ gamma \），对于所有值的所有网络类型 -。

机器学习模型

图形神经网络是一类模型，适用于将节点特征作为结构信息的图形上的机器学习任务^{64，，，，65}。基于通过可学习功能汇总和更新节点信息的基本思想，图形神经网络产生了许多变体，例如图形卷积网络⁶⁶，图形注意网络⁶⁷，图形同构网络⁶⁸和图形变压器⁶⁹。它们已被广泛应用于节点分类等问题⁷⁰，结构推断⁷¹，生成任务⁷²和组合优化任务⁷³在图表上。

我们使用图神经网络解决网络压缩问题的方法如图所示。 1。在这里，我们采用图形同构网络来汇总节点特征并决定节点的分组。同一组中的节点被压缩到超节点中。同样，它们的连接总和成为超级节点的加权自循环。当然，小组间连接塑造了不同超节点之间的加权链接。为了评估粗粒的有效性，我们比较了归一化分区函数的平均绝对误差（MAE），\（\ frac {z} {n} \）， 在哪里n是原始网络中的节点数量或压缩的节点数量。因此，MAE是我们用来训练图神经网络的损失函数。请注意，通过优化，模型可以使用梯度下降连续调整从节点局部结构特征到节点分组的映射。此调整可确保所得的宏观网络具有类似于原始网络的分区函数。

在这里，我们提到了我们模型的许多合适属性。首先，由于原始网络中的每个边缘都成为宏观网络中加权边缘的一部分，因此可以保证网络的连接性。如果连接了原始网络，则宏观网络也将连接。其次，宏观网络中的节点数量可以灵活地配置为可以调节以满足不同任务的超参数。最后，正如我们在下一部分中显示的那样，我们模型的时间复杂性是o（（n+ e）， 在哪里n和e分别是原始网络中的节点和边缘的数量。这是与其他经常执行的模型相比的相当优势o（（n³） - 包括盒子覆盖，拉普拉斯RG或o（（n²）例如，几何RG。因此，我们能够压缩非常大的网络。请看 补充材料有关时间复杂性的更详细分析（补充说明 7）和通过100,000个节点进行网络压缩的实验（补充图。 3）。

我们的方法与拉普拉斯重归其化组（LRG）的不同

由于两种方法都使用网络密度矩阵，因此有必要讨论其差异。LRG是最早基于网络扩散动力学作为重新归一化过程的核心而引入Kadanoff的分解的人之一。它已经成功地将RG的边界推向了结构异质性，这是在复杂系统中广泛观察到的特征。为此，LRG专注于特定的相位过渡范围的特定热量，以定义其信息核心^{52，，，，60}并使用它们进行重新归一化。

至关重要的是，LRG和我们的方法之间的差异不仅限于机器学习实现。相反，基本差异在于RG问题的理论概念化。我们基于以下事实，即该分区函数包含流量的宏观描述符的完整信息，包括网络熵和自由能，如前几节所示。因此，通过尝试在所有传播量表上复制完整的分区函数配置文件（所有值 -）我们复制宏观特征，例如扩散途径的多样性和到达网络遥远部分的流速。

值得一提的是，LRG可用于在任何特定规模上重新归一致（ -）。但是，它们丢弃了扩散过程的快速模式（对应于大于的特征值\（\ frac {1} {\ tau} \））。相反，我们的方法通过维护分区函数的全部行为，同时保留所有尺度的特征值的完整分布

最后，除了讨论的理论论点外，我们还使用各种数值证据证明我们的适用性领域比LRG大得多。如前所述，LRG专为Barabasi-Albert（BA）和无尺度树（Barabasi-Albert）等异质网络而设计。但是，现实世界网络的拓扑不限于BA模型可以生成的拓扑。网络科学的二十年已经揭示了现实世界的网络还表现出重要特征，例如隔离，同时集成和秩序，而混乱，即模块，主题等。这就是为什么压缩方法最终必须超出当前局限性和当前限制和特定于模型的假设。

在以下各节中，我们比较了NFC模型和其他广泛使用的方法（包括LRG）在合成和经验网络上的性能。请参阅补充说明 3有关信息流的保存的不同数据集，与LRG进行了更详细的比较（补充图。 5）和熵（补充图。 7），保留特征值分布（补充图。 6），以及超节点组成的差异（补充图。 8）和宏观网络结构（补充图。 9）â比较清楚地显示了我们的方法和LRG之间的巨大差异，无论是在性能和​​它们将节点组合在一起的方式上。

合成网络压缩

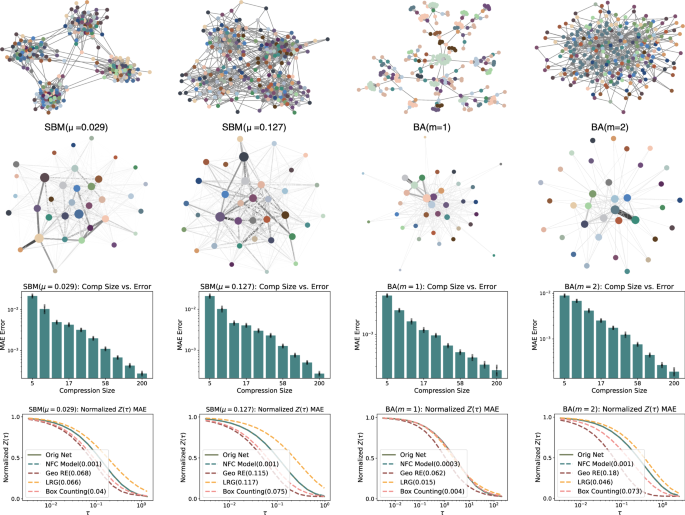
在这里，我们使用模型来压缩四个合成网络：两个随机块模型（SBM），带有混合参数（¼）0.029和0.127，以及两个带有参数的BarabãsiAlbert（BA）m= 1，2，全部带有256个节点（见图 2）。正如预期的那样，对于非常大的压缩，我们发现分区功能之间的偏差有所增加，即成本。

但是，有趣的是，压缩误差与网络大小表现出大致无规模的关系，这意味着没有压缩大小是特殊的。我们在图中的第二行子图中使用35个节点可视化压缩网络。 2，在压缩网络中的节点和原始网络中的相应节点分配了相同的颜色。

我们表明，我们的方法的表现优于其他方法，包括盒覆盖，几何重归于和拉普拉斯的重生。同样，我们的结果表明，SBM的中尺度结构和BA中的集线器的存在在结果压缩网络的拓扑中起重要作用。原始SBM网络中属于同一社区的节点通常会组合在一起，以在宏网络中形成超级节点。更令人惊讶的是，在BA网络中，具有相似连接数量的节点通常是粗粒的。

这一发现表明，无论是否直接连接，具有相似局部结构的节点都需要在目标恢复信息流时组合在一起。在这里，模型自动学习了具有相似局部结构的节点的粗粒，并且没有预先确定的先验。

经验网络压缩

我们分析了两个代表性的经验网络，以测试我们方法的能力。网络包括美国机场公开航班和Netzschleuder，以及2006年使用的科学家共同创作网络⁷⁴。

在美国机场网络中，节点和边缘代表了它们之间的机场和飞行路线，即，如果它们之间至少有一次航班，则二进制和无方向的边缘连接两个机场。同样，在共同作者网络中，节点是个别研究人员，如果两个科学家共同撰写了至少一篇论文，则存在优势。（有关数据集的更多详细信息，请参见表 1）。

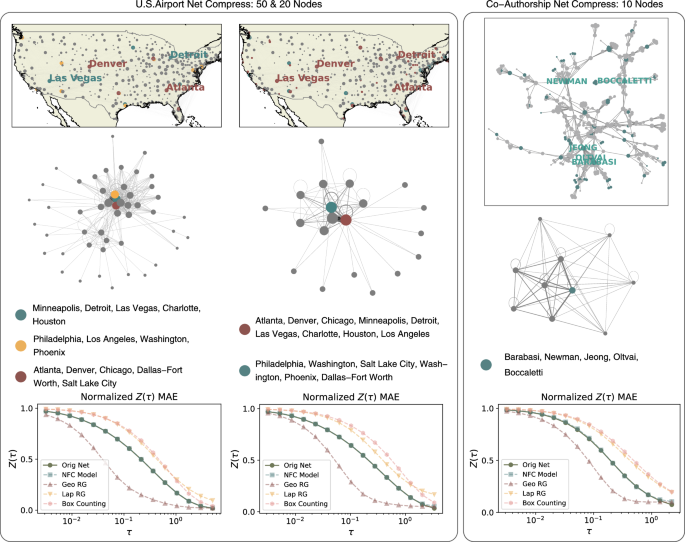
首先，我们将美国机场网络最多减少50和20个超节点压缩尺寸（见图 3）。我们强调了连通性最高的15个机场，位于亚特兰大，丹佛，芝加哥，达拉斯 - 沃思，明尼阿波利斯，底特律，拉斯维加斯，夏洛特，夏洛特，休斯敦，费城，洛杉矶，洛杉矶，华盛顿，盐湖城和菲尼克斯的城市。有趣的是，这15个机场组合在一起，仅形成了几个超节点，这是由于它们相似的本地结构，即在这种情况下，在这两种压迫中。此外，在50个节点的宏观网络中，亚特兰大和丹佛等城市被压缩成一个超节点，底特律和拉斯维加斯等城市形成了另一个超级节点。而在具有20个超节点的压缩中，包括亚特兰大，丹佛，底特律和拉斯维加斯在内的城市加入了一个超级节点。

美国机场网络和科学家的共同创作网络（2006）以及不同宏节点配置下的相应压缩结果。我们进一步说明了与节点学位确定的与前15个机场和前5个科学家相关的宏节点，其中一些顶点在原始网络中标记。显然，这些最具象征性的节点主要集中在有限数量的宏节点中，这支持了以下假设：具有相似局部结构的淋巴结呈现出相似的组。随着宏机场网络的收缩，这些节点融合成较少的宏节点，这表明宏网络的表达性降低需要该模型忽略这些节点之间的区别。随后的三个子图描绘了从我们的方法中，在压缩结果中，归一化分区函数的平均绝对误差（MAE）针对其他竞争方法得出。值得注意的是，由于某些比较方法（例如盒覆盖）无法精确控制压缩后网络的大小，因此我们允许它们压缩大于目标大小的网络并将其与我们的方法进行比较。

网络科学家系统的压缩证实了先前的结果（见图。 3）。例如，该数据集的五个最高学位研究人员，包括Barabasi，Jeong，Newman，Oltvai和Boccaletti，形成一个超级节点，当宏观网络的大小为10时，请注意它们不是一个与紧密连接的组。原始网络。实际上，纽曼，巴拉巴西和博卡莱蒂甚至在这个网络中都没有连接。这进一步表明，网络中具有相似的本地结构是压缩的关键因素。

最后，我们比较了通过不同的压缩方法实现的分区函数偏差，并表明我们的方法明显优于他人（见图 3），在两个经验系统的情况下。有关所有机场分组的更多详细信息，请参阅补充表格 1。

总体而言，确认合成网络分析，我们的方法通过相似的本地结构的粗粒节点生成了宏网络，与原始网络中的信息流非常相似。

压缩过程的解释性

在与合成网络和现实世界网络的实验中，我们发现我们的机器学习模型将节点与相似的本地结构合并以保持信息流。在这里，我们试图提供有关其确切工作方式的解释。

首先，与局部结构相似的聚类节点共同保留了原始网络中该局部结构的功能，同时降低结构冗余。通过分析几种典型拓扑特征，可以直观地理解这一点。

高聚类系数节点

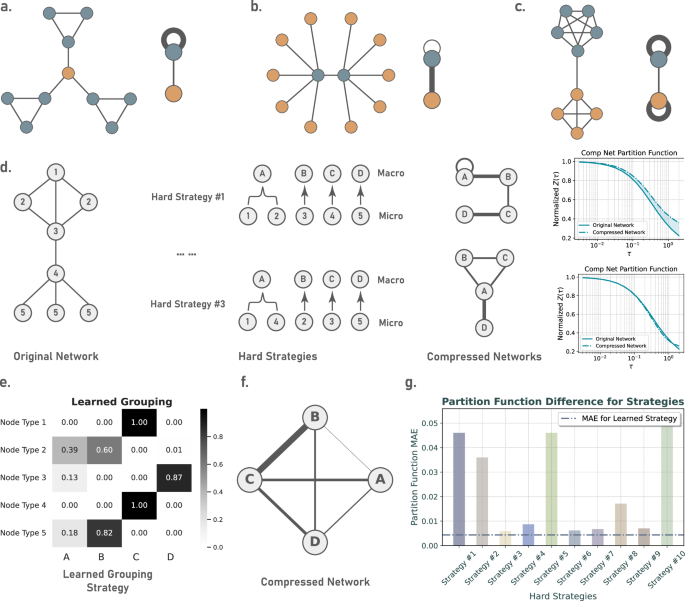
具有较高聚类系数的节点通常具有相互联系的邻居，在网络中信息传播过程中局部捕获信息。将节点与高聚类系数分组在一起，它们的众多互连将成为超级节点上的高重量自我循环，同样在本地捕获信息中发挥了作用，如图所示。 4，子图一个。

具有高聚类系数的节点的压缩的说明。高簇节点及其相应的宏节点都倾向于在本地捕获信息。bDemonstration of the compression of hub nodes. Both the hub nodes and their corresponding macro-nodes act as bridges for global information diffusion.cCompression of community structures: Nodes within the same community are compressed into a supernode, which, similar to the original community structure, tends to trap information locally. dWe show the macroscopic network after compression using different hard(discrete) grouping strategies for a toy network with 8 nodes and 5 types of different local structures, and the changes in the corresponding partition function.eThe soft(continuous) grouping strategy learned by our model.在 （f) we present the macroscopic network structure given by the grouping strategy from (e）。gComparison of the normalized partition function error before and after compression under different grouping strategies.集线器

Hub nodes act as bridges for global information diffusion within the network. By clustering hub nodes together, the edges between hub nodes and other nodes transform into connections between supernodes in the compressed network, still ensuring the smooth passage of global information. Suppose we group a hub node and its neighbors into one; then, their interconnections become self-loop of that supernode that trap the information locally, acting as a barrier to global information transmission, as shown in Fig. 

4, subplotb。Strong communities

Networks with distinct community structures experience slow global information diffusion (due to few inter-community edges). Grouping nodes of the same community together transforms the numerous intra-community edges into self-loops on the supernodes, trapping information locally. Meanwhile, the few inter-community edges become low-weight edges between supernodes, similarly serving to slow down the speed of global information diffusion as shown in Fig. 

4, subplotc。Through these three typical examples, we find that structural redundancy has been reduced while the corresponding functions are preserved.Therefore, this approach naturally benefits the preservation of information flow when compressing networks.

Then, based on the principle that “nodes with similar local structures are grouped together," the graph neural network still needs to optimize the specific grouping strategy. This is mainly because, on one hand, the number of groups is often far less than the number of types of nodes with different local structures (imagine a network with 3 different types of nodes, whereas we need to compress it into a macro network with 2 nodes). On the other hand, our model produces continuous grouping results, for example, a certain type of node might enter group A with an 80% ratio and group B with a 20% ratio. Each different ratio represents a new grouping strategy, and we need to find the most effective one from infinitely many continuous grouping strategies, which is an optimization problem, hence requiring the aid of a machine learning model. Subplotsd − fof Fig. 4show discrete grouping strategies and the learned continuous grouping strategy for compressing a network with 5 types of nodes into a macroscopic network with 4 supernodes.From Fig. 4

, we can see that different discrete grouping strategies produce different macroscopic network structures (subplotd), our learned continuous grouping strategy (subplote), the macroscopic network structure (subplotf), and the partition function difference corresponding to different grouping strategies (subplotg）。It is evident from the figure that the error in preserving information flow with our learned continuous grouping strategy is lower than that of all discrete grouping strategies.In summary, this is how our model works: based on the fundamental useful idea that “nodes with similar local structures enter the same group," our model uses the gradient descent algorithm to select one of the infinitely many solutions (continuous grouping strategies) that results in a lower error of the partition function.Compressing networks from different domains

To further explore the applicable fields of our model, we conducted further analysis on various real networks and attempt to understand the differences in compression outcomes across different domains. In our upcoming experiments, we have selected 25 networks from 8 different fields: biological networks, economic networks, brain networks, collaboration networks, email networks, power networks, road networks, and social networks. Their node number ranges from 242 to 5908, and the number of edges ranges from 906 to 41,706. See Supplementary Table 

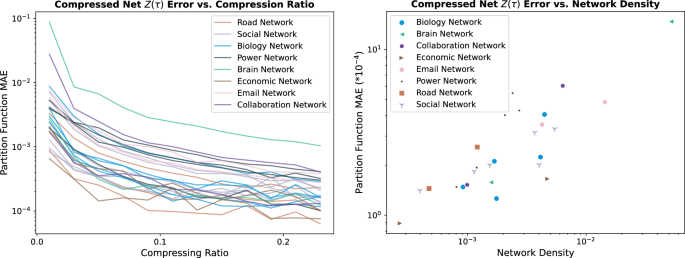
2for more information of these networks.We compressed all networks at various scales, with compression ratios ranging from 1% and 2% up to 25% of the original network size. We aimed to explore how the effectiveness of compression varies with the compression ratio across networks from different domains. The results are shown in the left subplot of Fig. 

5。First, we observed that in most of the cases, the error of the normalized partition function (measured by Mean Absolute Error) is less than 10−2^{, indicating that our model performs well across networks from different domains. Moreover, regarding the differences between networks from various domains, we found that the density of the network has a major impact on compression efficiency. As shown in the right subplot of Fig.Â} 5, we plotted the density against the error in the partition function before and after compression for all networks, and observed a positive correlation(correlation coefficient of 0.856): a network with lower density tends to be more easily compressed. It is plausible that this happens because an increase in the number of connections makes the pathways for information transmission more complex, thereby increasing the difficulty of compression.Fig. 5: Compressing empirical networks from different domains.

One compression model for many real-world networks

In previous sections, a separate GNN was trained to learn a compression scheme tailored to a specific network. Despite the satisfactory compression results, learning a new neural network for each dataset can be computationally costly. Therefore, we generalize the previous model and train it on a large set of empirical networks. We show that this generalization can compress new networks, the ones it hasn’t been trained on, without any significant learning cost.

First, we gather a dataset with 2, 193 real-world networks spanning various domains, from brains and biological to social and more, with the number of nodes ranging from 100 to 2, 495, from Network Repository (NR)

75^{(for more information about the dataset, training, and testing process, please see Supplementary NoteÂ} 6）。We randomly select the networks with size smaller than 1000 as the training set and keep the remaining networks as the test set.We apply one model to numerous networks, compress them to macro-networks, and calculate the loss in terms of partition function deviation.The results demonstrate highly effective learning that can successfully compress the test set, generating macro-networks that preserve the flow of information.

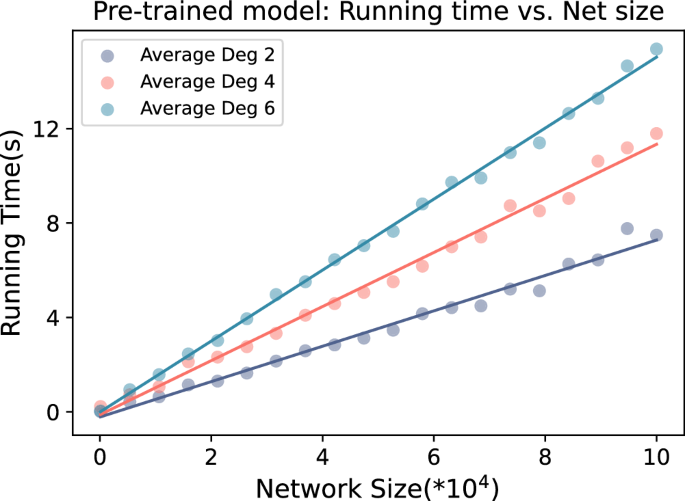
This pre-trained model directly possesses the capability to compress networks from different domains and sizes, and it reduces the computational complexity by orders of magnitude, outperforming existing methods. More technically, the time complexity of our model iso（（n + e）， 在哪里nis the system’s size andethe number of connections – which overall drops too（（n) for sparse networks – while the time complexity of other compression models often reacheso（（n³) (box-covering, laplacian RG) oro（（n²)(geometric RG). To better quantify the model’s time complexity, we validated it on a dataset with a much wider range of sizes. The results are shown in Fig. 6。

In this figure, we show the time required for a pre-trained model to run on W-S networks with different numbers of nodes and connections. The X-axis represents the number of nodes, and the Y-axis shows the time needed to compress the network.

In network compression methods, a method that can accurately preserve the full properties of the network information flow across different structural properties is still missing. Traditional methods rely on sets of rules that identify groups of nodes in a network and coarse-grain them to build compressed representations. Instead, we take a data-driven approach and extract the best coarse-graining rules by machine learning and adjusting model parameters through training. In contrast with most network compression methods that try to maximize the structural similarity between the macro-network and the original network, our model tends to preserve the flow of information in the network and, therefore, is naturally sensitive to both structure and dynamics.

To proxy the flow of information, we couple diffusion dynamics with networks and construct network density matrices— i.e., mathematical generalizations of probability distributions that enable information-theoretic descriptions of interconnected non-equilibrium systems. Density matrices provide macroscopic descriptors of information dynamics, including the diversity of pathways and the tendency of structure to block the flow. Here, we show that similar to equilibrium statistical physics, the network counterpart of the partition function contains all information about other macroscopic descriptors. Therefore, to preserve the flow of information through the compression, we train the model using a loss function that encodes the partition function deviation of the compressed system from the original networks.

We use the model to compress various synthetic networks of different classes and demonstrate its effective performance, even for large compressions. Then, we analyze empirical networks, including the US airports and researchers’ collaborations, confirming the results obtained from the analysis of synthetic networks.

Our work shows that one way to preserve the information flow is to merge the nodes with similar local structures. With this approach, we can reduce redundant structures while preserving the function of these structures in the original network. Note that this result is an emergent feature of our approach and not an imposed one. One significant feature of our method is that it is not constrained to localized group structures: units that are merged together through the compression process are not necessarily neighbors and can even belong to different communities.

We train the neural networks on thousands of empirical networks and show the effectiveness of generalization and excellent performance on new data. This results in a significant reduction in time complexity. While the time complexity of other compression models often reacheso（（n³) (box-covering, laplacian RG) oro（（n²)(geometric RG), our approach reduces it too（（n + e）， 在哪里nis the number of nodes anderepresents the number of edges, enabling our approach to compress networks of sizes that are unmanageable by other approaches. Therefore, our work demonstrates the feasibility of compressing large-scale networks.

Despite these advantages, our model still has limitations. While it can flexibly handle network structures from different domains, the statistical characteristics of networks also affect the model’s performance. Our experiments on more real network data have shown that denser networks are harder to preserve the partition function after compression. Furthermore, although we have proven that the model can preserve information flow, we cannot guarantee the preservation of all structural features. Experiments have shown that we can maintain the scale-free nature of the degree distribution after compressing BA networks, but we still cannot ensure the preservation of other important structural properties (see Supplementary Fig. 11for related experiments).

Our work combines recent advances in the statistical physics of complex networks and machine learning to tackle one of the most formidable problems at the heart of complexity science: compression. Our findings highlight that to compress empirical networks it is required that nodes of similar local structures unify at different scales, behaving like vessels for the flow of information. Our fast and physically grounded compression method not only showcases the potential for application in a wide variety of disciplines where the flow within interconnected systems is essential, from urban transportation to connectomics, but also sheds light on the multiscale nature of information exchange between network’s components.

Training methodology

Our model is trained in a supervised learning manner, with our ultimate supervision objective being to ensure as much similarity as possible between the partition function curves of the macro and original networks. The partition function, a function of time, ultimately converges. In principle, we cannot directly compare and calculate losses between two functions. Therefore, we uniformly select ten points from the logarithmic interval of time before the partition function converges, composing a vector as the representation of the partition function. The aim is to minimize the Mean Absolute Error (MAE) between these two vectors.

In most scenarios, we also utilize another cross-entropy loss function to expedite the optimization process. Specifically, we randomly select two rows (indicating the grouping status of two nodes) from the grouping matrix and compute their cross-entropy, aiming to maximize this value as an alternative optimization objective. This loss function encourages the model to partition distinct nodes into separate supernodes, thereby accelerating the optimization process. The final loss function is determined by a weighted sum of this cross-entropy optimization objective and the similarity of the normalized partition functions, with different weights assigned to each.

模型参数

In this section, we delineate the hyperparameters used during model training, enabling interested readers to reproduce our experimental results. Generally speaking, our model does not exhibit particular sensitivity towards hyperparameters.

• Hyperparameter Settings for Network-Specific Compression Model

  • Epochs: we train the model for 15000 epochs until it converge;

  • Activation function: ReLU Function

  • Each layer learns an additive bias

  • Hidden neurons in GIN layer: 128

  • Num of layers in GIN: 1

  • Learning Rate: fixed to 0.001

  • Weight for loss functions: 0.99 for partition function loss and 0.01 for cross-entropy loss

• Hyperparameter Settings for Compression Model for multiple networks

  • Epochs: we train the model for 3000 epochs until it converge;

  • Activation function: ReLU Function

  • Each layer learns an additive bias

  • Hidden neurons in GIN layer: 128

  • Num of layers in GIN: 1

  • Learning Rate: fixed to 0.001

  • Weight for loss functions: 0.99 for partition function loss and 0.01 for cross-entropy loss

Two target functions

Our model’s overall goal is to compress network size while ensuring the normalized partition function remains unchanged, with different normalization methods leading to different specific target functions. Assuming the original network hasnnodes with a partition functionz, and the compressed network has\({N}^{{\prime} }\)nodes with a partition function\({Z}^{{\prime} }\), the two target functions are\(\frac{Z}{N}=\frac{{Z}^{{\prime} }}{{N}^{{\prime} }}\)和\(\frac{Z-1}{N-1}=\frac{{Z}^{{\prime} }-1}{{N}^{{\prime} }-1}\)。Under all other equal conditions, the former target allows us to derive a relationship for the change in entropy as\({S}^{{\prime} }=S-log(N/{N}^{{\prime} })\)， 在哪里\({S}^{{\prime} }\)denotes the entropy of the compressed graph, meaning the shape of the entropy curve remains unchanged after compression (see Supplementary Fig. 7for numerical results). The latter ensures that the normalized results of the partition function range from 0 to 1, better preserving the original network’s eigenvalue distribution (see Supplementary Fig. 12for experimental results). Unless otherwise specified, all results presented in the paper and补充材料are obtained under the first target function. We have also conducted experiments using the second target function; please refer to the Supplementary Fig. 13for results on synthetic network compression results by the second target function. By setting different target functions, we have enriched the methods of network compression from different perspectives.

报告摘要

Further information on research design is available in the Nature Portfolio Reporting Summary链接到本文。

作者注意

1. These authors contributed equally: Zhang Zhang, Arsham Ghavasieh.

作者和隶属关系

1. School of Systems Science, Beijing Normal University, Beijing, China

   Zhang Zhang & Jiang Zhang

2. Swarma Research, Beijing, China

   Zhang Zhang & Jiang Zhang

3. Department of Physics & Astronomy ‘Galileo Galilei’, University of Padua, Padua, Italy

   Zhang Zhang & Manlio De Domenico

4. Center for Complex Networks and Systems Research, Luddy School of Informatics, Computing, and Engineering, Indiana University, Bloomington, IN, USA

   Arsham Ghavasieh

5. Padua Center for Network Medicine, University of Padua, Padua, Italy

   Manlio de Domenico

6. Istituto Nazionale di Fisica Nucleare, Sez., Padova, Italy

   Manlio de Domenico

贡献

M.D.D conceived and directed the project, Z.Z and J.Z designed the model, M.D.D and A.G conducted the theoretical analysis.Z.Z conducted the experiments.M.D.D, Z.Z and A.G wrote the paper.所有作者都讨论了结果并评论了手稿。

相应的作者

对应Zhang Zhang或者Manlio de Domenico。

竞争利益

作者没有宣称没有竞争利益。

同行评审信息

自然通讯thanks Angeles Serrano, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.提供同行评审文件。

开放访问本文已根据创意共享归因非商业 - 非涉及商业4.0国际许可证获得许可，该许可允许以任何媒介或格式的任何非商业用途，共享，分发和复制，只要您对原始作者提供适当的信誉and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material.您没有根据本许可证的许可来共享本文或部分内容的改编材料。The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.要查看此许可证的副本，请访问http://creativecommons.org/licenses/by-nc-nd/4.0/。重印和权限

关于这篇文章