机器学习间原子潜能中炼金术自由度的插值和差异

原子模拟是材料动态行为的计算建模的基石。实现预测性和有效的仿真需要在描述原子间相互作用的质量和成本之间取得平衡，以实现收敛的热力学平均值。密度功能理论（DFT）计算通常被视为材料模拟准确性的金标准。从头算分子动力学（AIMD）模拟¹使用这些高质量的DFT力来传播动力学，但它们的高计算成本限制了可扩展性。机器学习间的潜力（MLIP）^{2，，，，3}，经过电子结构计算结果训练，提供了MD中DFT能量和力的低成本替代品。从Beller parrinello网络的开创性作品开始⁴和差距⁵，已提议各种MLIP体系结构在准确性和速度之间的权衡中提供选择，例如Schnet⁶，潘恩⁷，nequip⁸，Allegro⁹，狼牙棒^{10，，，，11}和cace¹²。最近，通用MLIP，例如M3GNET¹³，Chgnet¹⁴和MACE-MP-0¹⁵，已经出现了，在周期表及其组合中提供了大部分元素的原子建模能力。所有这些模型均经过DFT能量和从大规模材料数据库中提取的梯度（例如材料项目）培训¹⁶。基准结果^{17，，，，18}证明它们提供了原子相互作用和声子分散的高保真建模，从而在下游原子模拟应用程序的背景下充当可靠的基础模型。

虽然原子间电位主要旨在在具有固定元素身份的原子位置上运作，但考虑其炼金术自由度的吸引力，其中可以连续改变元素身份。在电子结构方法的领域中，冯·利林菲尔德（Von Lilienfeld）及其同事率先开创了分子大典型合奏集合DFT，并在炼金术转化方面进行了进步的研究线，这可以改变和优化化学成分^{19，，，，20，，，，21，，，，22，，，，23}。从MLIP的角度来看，Ceriotti及其同事基于原子中心的密度框架引入了炼金术压缩方案，并将方法应用于模型高渗透合金^{24，，，，25，，，，26}。他们证明，将物理元素的表示在伪元素的低维子空间上，可以有效地建模构图复杂的系统和插值，以在训练过程中未遇到的元素。此外，Chen等。²⁷证明可以通过使用低维元素嵌入的线性插值来将预训练的材料性能预测变量应用于无序晶体。虽然元素的连续表示对应于基于图的MLIP中的原子嵌入，但大多数通用MLIP通常使用更高维的原子嵌入来确保模型足够表达。由于模型仅受过离散原子身份训练，因此在识别有意义的元素嵌入的亚体以插值元素或项目梯度是挑战²⁸。另一方面，用于建模组成的嵌入的简单线性插值可能会导致非物理输出。

炼金术变化在自由能模拟中尤其重要^{29，，，，30}。自由能模拟被广泛用于表征固相的有限温度稳定性^{31，，，，32}，并且已经开发了自动协议³³。但是，虽然炼金术自由能计算被广泛用于研究蛋白质小分子相互作用³⁴，它们在材料系统中的应用是有限的。这很大程度上是由于针对具有三个或更多元素的系统的参数性原子势的挑战。值得注意的是，Jinnouchi等。³⁵引入了热力学整合（TI）方法，以计算H中液体Si和LIF的化学电位₂o通过炼金术开关平稳地打开或关闭基于内核MLIP的原子之间的相互作用。

随着通用MLIP的出现，拟合包含多种类型元素的系统的挑战已得到缓解，它们为平衡几何形状周围的动力学提供了合理的准确性。因此，及时考虑使用通用MLIP来促进沿炼金术途径的自由能模拟。在这项工作中，基于原型MLIP的典型结构，我们访问了MLIPS固有的迄今为止隐藏的炼金术自由度。我们没有通过引入炼金术原子来增强输入图结构，而不是改变单个原子的连续嵌入，每种都与其各自的组成重量相关联。通过随后对消息传递方案和能量读数的修改，我们的方案在不同材料的组成状态之间提供了平滑的插值。而且，鉴于相对于炼金术重量的端到端的可不同性我”，它有助于计算能量的炼金术梯度h/我”然后计算炼金术转化的自由能。此外，我们探讨了具有混合成分的炼金术中间状态的应用，以创建对实心解决方案的计算有效描述。

炼金术图和消息传递

原型MLIP结构

我们的目的是将修改MLIP的不可行部分引入修改，以便我们可以在材料的炼金术组成的情况下对模型进行建模。首先，我们首先引入基于图的MLIP的典型结构。原子系统表示为图\（{{{{\ Mathcal {g}}}}} =（{{{{\ Mathcal {V}}}}}}}}，{{{{\ Mathcal {e}}}}}}}}}}}}）\）用原子作为节点\（i \ in {{{\ Mathcal {v}}}}} \）\）以及在定义的截止距离内的原子对作为边缘\（（i，j）\ in {{{\ Mathcal {e}}}}} \）\）^{36，，，，37}。每个元素z_我嵌入到连续的矢量中z_我，然后用来初始化节点功能\（{{{{\ boldsymbol {h}}}}}}} _ {i}^{（0）} \）。边缘功能e我_{j是从相对位移得出的}r我j_{。然后，输入通过带有消息的机制通过图神经网络的层}38^{，，，，39，，，，40。在层中}t，一条消息\（（{{{{\ boldsymbol {m}}}}}}} _ {i}^{（t）} \）是通过在相邻节点上汇总消息贡献来构建的\（{{{\ Mathcal {n}}}}}（i）\）作为$$ {{{{\ boldsymbol {m}}}}}}} _ {i}^{（t）} = {\ sum} _ {j \ in

从隐藏的节点功能和消息函数中计算出每个贡献的位置m_t。然后，这些消息用于更新节点功能：

在哪里你_t是一个更新功能。最后，读取功能r转换最终节点功能\（（{{{{\ boldsymbol {h}}}}}}} _ {i}^{（t）} \）进入节点能量，在整个节点列表中求和，以估算势能

这是MLIP的最小原型，最先进的模型使用各种其他机制来增强表达性，以改善训练数据的拟合度。尽管这项工作中引入的炼金化修饰是基于此原型的，但可以很容易地将其与其他机制集成在一起，这在“方法中进一步详细介绍”。

炼金术修饰

现在，我们将修改介绍给输入图和MLIP模型的体系结构，以允许与原子部分占用的构图混合结构进行建模。主要思想是用炼金术零件增强原始图，为要建模的每个构图状态创建额外的原子或节点，并修改消息传递方案，以使其与基线MLIP保持一致。首先，我们定义炼金术重量\ \（{{{{\ boldsymbol {\ lambda}}}}}}} = {\ {{{\ lambda} _ {\ alpha}}} _ {\ alpha}} _ {\ alpha = 1}为每个组成状态分配权重。例如，如果我们以20％，30％和50％的重量对LICL，NACL和KCL的混合结构进行建模，则权重为我”[0.2，0.3，0.5]。

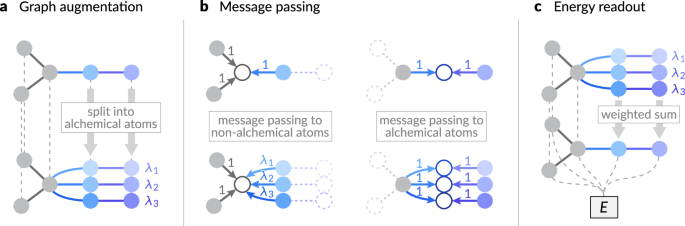
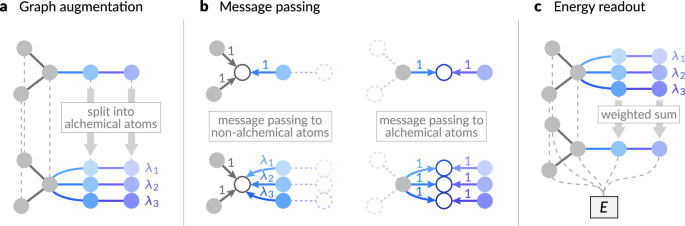
现在，我们定义了炼金术图\（\ tilde {{{{{\ Mathcal {g}}}}}}} =（\ tilde {{{{{{\ Mathcal {v}}}}}}}}}，\ tilde {作为原始图的扩展\（{{{{\ Mathcal {g}}}}} =（{{{{\ Mathcal {V}}}}}}}}，{{{{\ Mathcal {e}}}}}}}}}}}}）\）。对于上一个示例，我们假设我们具有代表NaCl晶体结构的原始图。该构建独立于炼金术原子的原始元素身份，只有原子位置将继承。炼金图中的每个节点都通过一对索引（原子索引）识别我和炼金指数±并由\（（i，\ alpha）\ in \ tilde {{{{{\ Mathcal {v}}}}}}}} \）\）。所有非化学原子（例如Cl）（例如Cl），对于所有组成状态，该元素都相同，均分配±= 0，相应的重量我”₀=1。炼金原子根据其组成态分为多个节点（图 1一个）。例如，na原子我在原始图中，分为三个节点（我，1），（我，2）和（（我，3），带有元素（z（（我，1）_{，一个 z（（}我，2）_{，一个 z（（}我，3）_{）=（li，na，k）。因此，将用各自的元素嵌入来初始化炼金术原子的节点特征。然后，我们分配了炼金术重量}我”±_到节点（我，一个 ±）。所有其他特征，例如原子的位置，都从原始图，例如，例如，r（（_{我，一个 ±）=} r我_。图1：机器学习间原子电位的炼金术修饰方案。

炼金术图增强：相关的原子原子分为具有不同元素身份的炼金术原子，与炼金术重量相关我”我。_b炼金术消息传递：在消息汇总步骤中（等式（等式）（（6）），根据等式中的不对称加权方案，对相邻原子的每个消息贡献进行加权。（（5）。只有根据源原子的炼金重量加权从炼金术到非化学原子的权重，以确保与原始图中的消息填充方案保持一致。c炼金术能读数：炼金术原子的能量贡献根据其各自的炼金术权重加权，以产生结构的总能量预测（称为e）。当任何两个端点节点都是非化学（带重量索引0）或两个节点处于相同的炼金术状态（具有相同的重量索引），即，即，即相同的炼金术，即相同，即，两个端点节点是非化学的（即具有相同的重量索引），即

$ \ begin {array} {rc} \ tilde {{{{{\ Mathcal {e}}}}}}}} = \ lest \ lest \ {（（i，\ alpha），（\; j，\ beta），（\; \ beta））\ right。

这与炼金术自由能文献中广泛使用的双重拓扑范式一致^{41，，，，42，，，，43}，其中不同炼金术状态中的原子在几何上并存，但不会直接相互作用。为了建模炼金图中原子之间的缩放相互作用，我们引入边缘权重以扩展消息贡献。Aldeghi和Coley⁴⁴提出了一个类似的想法，它们通过加权（随机）边缘在单体中的连锁原子之间对聚合物的不同拓扑组件进行建模。在这里，我们使用给定的不对称加权方案

即，仅炼金原子到非化学原子的信息贡献是由源原子的炼金重量加权的。此选择基于图中所示的观察结果。 1b。由于我们将原始MLIP扩展为炼金术组成而不修改可学习的功能，因此我们应确保传递的消息与所有边缘权重的原始图是一致的。根据炼金学原子的扩展和边缘连接方案的扩展，只有从炼金术原子传递到非alchemical Atom的信息，将其划分为多个alchem selode Alch and clote node and close node node。因此，在这种情况下，我们利用炼金术节点的权重作为边缘权重，并根据等式修改消息聚合方案。（（1）作为消息贡献的加权总和：$$ {{{{\ boldsymbol {m}}}}}}} _ {（i，\ alpha）}^{（t）} = {\ sum} _ {（j，j，\ beta）\

最后，能量预测的读数（等式（等式）（（3））被修改为炼金术节点贡献的加权集合（图 1c）：

请注意相同m_t和r如等式中的功能。（（1） 和 （3）使用，即没有修改可训练的权重。这种修改方案确保了原始MLIP方案的两个基本一致性。首先，当所有炼金术元素都是相同的时（z_{（（我，一个 ±）}= z_我）对于每个原始原子和炼金术重量最多1（\（{\ sum} _ {\ alpha = 1}^{k} {\ lambda} _ {\ alpha} = 1 \）），预测的势能与原始图相同。其次，当只有一种炼金术权重1（我”_±= 1），而其他则为零，预测的势能也与原始图中的元素组成相同z_±。在限制案例中，这两种一致性确保了组成状态之间的正确插值，尽管这里的论点基于原型MLIP，但在适应其他体系结构时，仍然存在一致性，如在“体系结构特定修改”和“补充信息。我们还探讨了替代性插值方法，包括嵌入插值，并比较它们在MLIP能量输出中的能力 补充信息。

固定溶液的表示

晶格参数

首先，我们研究了我们对组成态的混合物是否可以用于对固体溶液进行建模并优化其相对于组成的特性。尽管可以通过实心溶液的设计选择来调整许多晶体性能⁴⁵，在这里，我们将使用晶格参数来探测建模能力。从经验上讲，通过Vegard的定律所述，可以通过线性插值的固体溶液的晶格参数近似于固体溶液的晶格参数。^{46，，，，47}。然而，有些系统与这种理想的线性行为表现出明显的正面或负偏差，我们评估所提出的方法是否能够预测这种趋势。

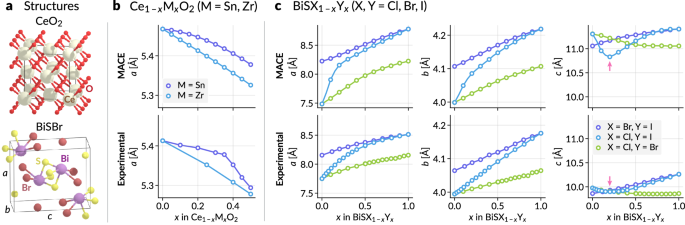
首先，Cutic CE的细胞参数_1xm_xo₂实心溶液表现出线性行为x当m = zr时，但显示为M = SN的扭结48^。我们从首席执行官开始建立了这种坚实的解决方案₂结构（图 2a），将CE原子分为两个炼金术状态，CE具有重量1 x和ZR或SN重量x，并通过放松单位单元格来优化零温度的单元格参数。适用于通用MACE-MP-0模型的炼金术方案¹⁵给出了M = ZR的正确线性行为，并成功识别了M = SN的阳性偏差（图。 2b）尽管它无法预测纠结。此外，我们还对正常BISX进行建模_1xy_x（x，y = cl，br，i）实心解决方案一个（肯定）和c（局部最小值负）表现出与线性的偏差49^。我们从Bisbr结构开始（图 2a）并将BR原子分为X和Y的两个炼金术原子。细胞参数通过各自的炼金重量进行了优化。例如，BISCL_1x我_x结构将具有炼金原子CL和I我”=（1 x，一个 x）。具有MACE模型的炼金术方案正确地识别了一个和c，分别为x = cl和y = i（图 2c）。特别是参数c比实验值大得多（由于原始MLIP的固有误差，本身可能是由于用于创建训练数据的PBE功能的不良性质而产生的），该局部最小值的组成（x准确预测了0.2）。尽管炼金术权重与实心溶液的化学计量学之间没有直接的对应关系，但这些结果表明，与Vegard定律的幼稚估计相比，此处开发的表示形式具有更大的预测精度。重要的是要注意，当前的方法假定了无限疾病，因此忽略了离子排序的效果。此外，由于所有炼金术原子都在父原子的位置合作，因此未考虑取代基原子的分数坐标之间的潜在差异。

起始结构，首席执行官2_{和Bisbr，用于实心解决方案。}b晶格参数一个力量1_xmxo₂（M = ZR，SN）作为组成重量的函数_x。c晶格参数一个，，，，b， 和c对于Bisx1xy_{x（x，y = cl，br，i）作为x}。_{上图是炼金术修改的MACE-MP-0培养基的结果}15，下面板是来自48^和49^{为了 （}b^{） 和 （}c）， 分别。最低面板中的箭头表示最小值c。源数据作为源数据文件提供。组成优化

大多数MLIP被设计为端到端可区分，以获得原子力和压力，作为相对于位置的势能的梯度

r我和应变张量_μ， IE。，f我=_e/r我和 _-= v1^e/μ在哪里v是系统的音量。梯度计算是通过自动分化产生的向后通过进行有效执行的50。^{凭借我们对组成状态的额外连续表示，炼金术重量}我”，我们还可以计算相对于组成的能量梯度e/我”。由于势能定义为恒定，因此物理上有意义的优化目标通常由能量差或能量梯度相对于某些系统变量给出。

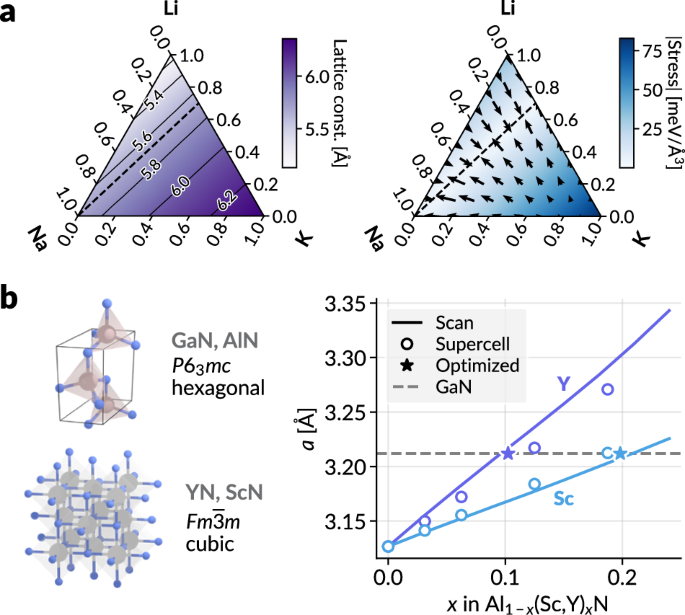
首先，我们考虑一个简单的模型：三个碱金属氯化物，licl，NaCl和KCl的固体解决方案。我们固定每个原子的分数坐标，并将立方晶格常数视为Li，Na和K的炼金术（或组成）重量的函数。为了找到与目标晶格常数相匹配的组合物，我们可以枚举一个组成和放宽固定成分的组合物，以使探针组合物的组合物与构图相比（比起构图）比起构图（比起。 3A，左）。但是，我们可以考虑将应力最小化，以最大程度地减少到优化的结构和组成。由于我们的方案是端到端的，我们可以计算绝对静水压力的梯度\（| {{{\ rm {tr}}}}} \，{{{\ boldsymbol {\ sigma}}}}}}} | /3 \）关于晶格常数固定到目标值的组成（图 3A，对）。然后，可以通过在组成空间上执行梯度下降，为设计问题提供不同的方法来找到最佳组成。这更有效，因为仅需要基于单个梯度的组成优化。在这种情况下，由于Na的大小在LI和K之间，因此在组成空间上存在多个最佳组成。

LICL，NACL和KCL实心解决方案的晶格参数优化。左图显示了优化的晶格参数作为颜色梯度，通过放松每个组成重量的细胞几何形状获得。右面板显示静水应力，其颜色强度代表应力幅度和指示梯度方向的箭头，这是通过将细胞尺寸固定到NaCl的尺寸来计算得出的。由于能量输出相对于炼金重量是可端到端的，因此可以优化组合物，以匹配目标细胞尺寸（最小化应力），通过遵循这些梯度。具有与NaCl（左）匹配的细胞参数的组合物以及通过在两个图中对齐的虚线指示的应力（右）获得的组合物。b实心解决方案的晶格匹配条件的优化1_xscxn和al_1xy_xn和gan。最稳定的多晶型结构显示在左侧。_{右侧的图显示了单元格的尺寸}一个通过优化每个成分重量（SCAN）获得一个GAN的值（优化）。所有结果均使用炼金术修改的MACE-MP-0培养基模型获得15。^{源数据作为源数据文件提供。}现在，我们将其应用于一个更现实的示例，我们想在其中找到实心解决方案的晶格匹配组合

1x_scxn和al_1xy_xn和gan。晶格匹配的组合物将促进这种固体溶液在GAN底物上的外延生长₅₁。^{目的是确定组成}x对于每个实体溶液，以便单元格参数一个晶格的匹配与GAN结构的值相匹配。尽管甘和阿尔恩具有六角形晶格（太空群p6₃mc），纯YN和SCN具有一个立方晶格（空间群\（fm \ + edline {3} m \）），这意味着一个人不能简单地在组成化合物的细胞参数之间插值来推断固体溶液的参数。在这里，我们修复了单元格参数一个对于六边形晶格，我们优化了相关的应力成分相对于细胞参数c以及al/sc或al/y/y组成（请参阅固体溶液的表示），因为掺杂的Aln会导致不同的c/一个比率。结果在图中 3b表明优化的成分是x0.1（y）和x0.2（sc），并且与正向扫描结果非常吻合，在扫描时，在扫描时测量了放松的细胞参数x值。此外，我们创建了一个4ââââââαAln的4 – 4超级细胞，然后随机切换一些Al原子到SC或Y原子以匹配目标组成并测量单位细胞参数。这些结果与炼金术单位细胞组成的扫描结果非常匹配，这表明当前工作中的方法也可以视为具有组成障碍的超级细胞的计算有效的紧凑表示。

混乱能量学

通过检查的数据集，可以进一步验证用于建模无序解决方案的炼金术MLIP的高计算效率和准确性\ \（{{{{{\ rm {a}}}}}}}} _ {2} {{{{{{\ rm {\ rm {\ rm {b}}}}}}}}}}^{{\ prime}}}}} {{{{\ rm {o}}}}}} _ {6} \）在我们最近的高通量研究中，多组分钙棍^{52，，，，53}。值得注意的是，\ \（{{{{{\ rm {a}}}}}}}} _ {2} {{{{{{\ rm {\ rm {\ rm {b}}}}}}}}}}^{{\ prime}}}}} {{{{\ rm {o}}}}}} _ {6} \）钙钛矿采用阳离子有序或阳离子限制的结构取决于各种阳离子有序构型的形成能量与阳离子序列的固体溶液的差异⁵²。对于有序结构，所有可能的对称不相等的阳离子排列的形成能量可以用作物理信息的描述，以预测实验阳离子障碍的热力学趋势⁵³。While DFT is computationally prohibitive for evaluating formation energetics of various enumerated cation-ordered atomic arrangements, we have shown that symmetry-aware equivariant graph neural networks, including equivariant MLIPs, provide efficient and accurate surrogates for assessing ordering-dependent thermodynamic stability in multicomponent perovskite oxides⁵²。

在这里，我们扩展了先前的分析，直接检查了完全阳离子序的形成能量\ \（{{{{{\ rm {a}}}}}}}} _ {2} {{{{{{\ rm {\ rm {\ rm {b}}}}}}}}}}^{{\ prime}}}}} {{{{\ rm {o}}}}}} _ {6} \）局部B位点占用率为0.5bâ²和0.5 b的固体解决方案â。传统上，特殊的quasirandom结构（SQS）^{54，，，，55}它优化了超级细胞中的元素位置以模仿随机合金的簇向量，已广泛用于研究无序的固溶性。尽管SQS方法为建模无序结构提供了系统的方法，但它需要大型超级电池以避免跨周期性边界的相关性，并依赖于诸如蒙特卡洛模拟的优化例程⁵⁶，限制了其对高通量研究的可行性。鉴于通过部分元素占用量代表疾病的炼金术修饰的MLIP的效率，我们使用基线MLIP进行了疾病模型的基线MLIP，将钙钛矿固体溶液与SQS细胞的炼金术单位细胞建模进行比较。

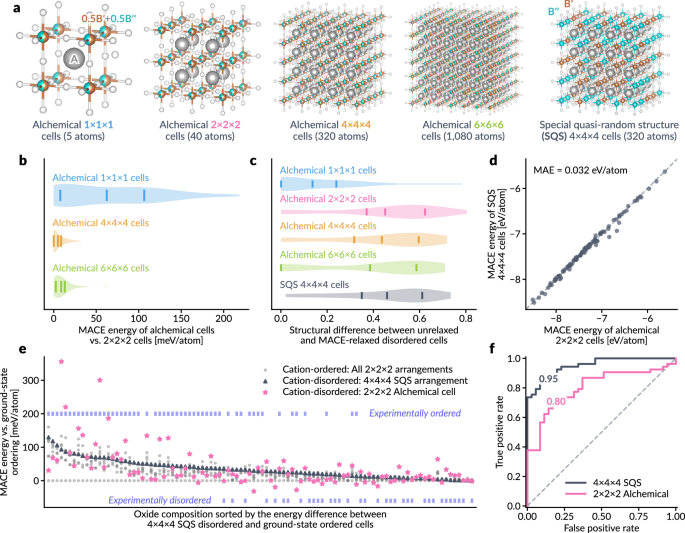
从基本订购的perovskite abo开始₃结构，我们将B原子分成两个炼金术物种，Bâ²和Bâ，每个分配的炼金重量为0.5。然后我们生成n -n -n（（n= 1，2，4，6）炼金术超级细胞和4ââ€4â€4平方英尺（图。 4a），使用炼金术修改的MACE-MP-0和基线MACE-MP-0模型优化每个单元。对于炼金术超级电池，在2â€2ã2超级电池处的每个原子pleateaus松弛的细胞能量，而与较大的超级电池相比，单位细胞（1ââ€1）的能量显着更高（图） 4b）。未延误和松弛无序细胞之间的结构差异，如图所示 4C，使用局部结构指纹的余弦距离进行定量^{53，，，，57}，揭示炼金术单位细胞仅略微放松，而较大的炼金术超级细胞和SQS细胞在相应的未省略和MLIP-RELAX的结构之间显示出更加显着的差异。如前所述^{52，，，，53}, crystallographic sites undergo substantial distortion during relaxation, such as octahedral tilting and Jahn–Teller distortions⁵⁸, which are typically beyond the periodicity of a perovskite unit cell and thus can hardly be captured by modeling a single unit cell.Given that the 2 × 2 × 2 supercell yields results similar to those of larger alchemical supercells, we proceed with further analysis using the 40-atom 2 × 2 × 2 alchemical supercell.

一个Crystal structure schematics for fully cation-disordered\({{{{\rm{A}}}}}_{2}{{{{\rm{B}}}}}^{{\prime} }{{{{\rm{B}}}}}^{{\prime}{\prime} }{{{{\rm{O}}}}}_{6}\)perovskite oxide solid solutions, illustrating different alchemical supercell sizes and number of atoms, and representative 320-atom 4 × 4 × 4 special quasirandom structures (SQSs).bMACE-relaxed energy differences between cation-disordered 2 × 2 × 2 alchemical cells and smaller or larger supercells, evaluated across 100\({{{{\rm{A}}}}}_{2}{{{{\rm{B}}}}}^{{\prime} }{{{{\rm{B}}}}}^{{\prime}{\prime} }{{{{\rm{O}}}}}_{6}\)compositions from⁵²。cDifference between the unrelaxed and MACE-relaxed structures for various alchemical cell sizes, including 4 × 4 × 4 SQSs, quantified by cosine distance between local structure fingerprints.Vertical bars represent the first quartile, mean, and third quartile, respectively.dComparison of MACE-relaxed energies for 2 × 2 × 2 alchemical cells versus 4 × 4 × 4 SQSs, with a mean absolute error (MAE) of 0.032 eV/atom.eMACE-relaxed energy differences among 2 × 2 × 2 alchemical cells, 4 × 4 × 4 SQSs, and all cation-ordered configurations with four B′ and four B″cations on eight B sites in the 2 × 2 × 2 supercell.Compositions are sorted by energy differences between 4 × 4 × 4 SQS and lowest-energy ordered arrangements.Experimentally characterized ordered and disordered compositions⁵³are marked in the upper and lower regions, respectively.fReceiver operating characteristic (ROC) curves for experimental order/disorder classification based on relative energy values of 4 × 4 × 4 SQS or 2 × 2 × 2 alchemical cells in (e) with respect to the lowest-energy cation-ordered arrangements, with area under the curve (AUC) values shown.All results are derived using the alchemically modified MACE-MP-0 medium model¹⁵。Source data are provided as a Source Data file.

As shown in Fig. 4d, the optimized single-point energies from the alchemical 2 × 2 × 2 supercell align well with those from the 4 × 4 × 4 SQS supercell, with a mean absolute error (MAE) of 0.032 eV/atom.Since the preference for cation-ordered and cation-disordered configurations depends on the relative formation energetics of each, we further compare energy values with all symmetrically inequivalent cation-ordered configurations in the 2 × 2 × 2 supercell, obtained by enumerating four B′ and four B″cations occupying eight B sites⁵³。The results in Fig. 4e show the relative energies of all considered structures, aligned with the ground-state (lowest-energy) cation-ordered structure energy as the reference.As previously discussed in refs.^{52，，，，53}, we observe that experimentally observed ordered compositions exhibit significant difference between the ground-state ordered configuration energy and other configurations, whereas experimentally cation-disordered compositions show similar energies among different configurations.The relative energy of the disordered SQS supercell provides a useful metric for characterizing experimental order/disorder, as seen by the separation of ordered and disordered compositions when sorting the oxide compositions by the SQS energy.Although the 2 × 2 × 2 alchemical supercell energies show more stochasticity, they follow the same trend as the relative energies of the SQS.This is further supported by the receiver operating characteristic (ROC) curves for experimental order/disorder classification based on relative energy values (Fig. 4f), where 4 × 4 × 4 SQS cell energies provide excellent classification with an area under the curve (AUC) of 0.95, while the alchemical 2 × 2 × 2 cell energies achieve reasonably good experimental order/disorder classification with an AUC of 0.80.The likely source of this difference is that for ions of very different sizes, local structural distortions are related to local chemical ordering, but the use of an average structure imposed by the alchemical method fails to produce local distortions that SQS captures well.

Hence, based on these results, we conclude that the alchemical modification of MLIPs offers a scalable approach for disorder modeling, as demonstrated with this multicomponent perovskite oxide dataset.The alchemical 2 × 2 × 2 supercells provide reasonable accuracy for experimental disorder classification, while using only 1/8 of the atoms in the 4 × 4 × 4 SQS supercells.Unlike SQS, these alchemical supercells can be obtained without the need for additional annealing steps for configuration generation.The results were achieved by modifying off-the-shelf pre-trained MLIPs and could be further fine-tuned to improve energy prediction and order-disorder classification.They may also be adapted for other material systems, including compositionally complex alloys and ceramics.

We also note that our approach shares similarities with the Virtual Crystal Approximation (VCA)^{59，，，，60，，，，61}, a traditional approach in modeling solid solutions with partial elemental site occupancy.VCA relies on two assumptions: (1) geometry: the solid solution is represented by an averaged structure where crystallographic sites are randomly occupied by different elements, disregarding local ordering;and (2) interaction: the random occupancy is approximated by compositionally weighted average of atomic pseudopotentials.Our method adopts the first assumption, making it subject to the same geometric limitations, such as the elements should be of similar size, occupy comparable positions, and local disorder effects should be minimal.However, the practical limitations of VCA mainly arise from what could be described as pseudopotential alchemy, where accuracy depends heavily on carefully tuning pseudopotential parameters like radial cutoffs and electronic configurations (core/valence).In contrast, our method sidesteps these challenges: MLIPs replace electronic structure calculations with iterative message-passing between node and edge features.Built-in regularization from training scheme and model architecture help ensure that results remain within a physically reasonable range, reducing the need for extensive manual parameter adjustments.

Free energy calculationsFree energy calculations

Here, we utilize the nonequilibrium switching method, where the Hamiltonian depends on a progression parameter

我”∈ [0, 1] so that it interpolates between the initial Hamiltonianh我 = h_（（我” = 0) and the final Hamiltonianhf = h（（_我” = 1).Assuming the NVT ensemble, the reversible work is given via the TI equation62：$$\Delta F={W}_{{{\rm{i}}}\to ^{{{\rm{f}}}}^{{{\rm{rev}}}}=\int_{0}^{1}{{{\rm{d}}}}\lambda {\left\langle \frac{\partial H}{\partial} \lambda }\right\rangle }_{\lambda }.$$

我”is switched from 0 at timet我to 1 at timet_f。The irreversible work done by switching the Hamiltonian is_{$${W}_{{{\rm{i}}}\to} {{\rm{f}}}}^{{{{\rm{irrev}}}}}=\int_{{t}_{{{{\rm{i}}}}}}^

在哪里\({E}_{{{\rm{i}}}\to {{\rm{f}}}}^{{{\rm{diss}}}\,}\)is the dissipated energy.In a linear-response regime, it can be shown^{63，，，，64}that the dissipated energy for the forward and backward path is the same when averaged over the transition path ensemble, i.e.,

Then, the free energy difference can be computed as

Often, the Hamiltonian is parametrized by the linear interpolation of the two endpoints, i.e.,h（（我”) = (1 − 我”）h我 + _我”hf, to simplify the calculation of the gradient term ∂h_/∂我”in Eqs.（（8） 和 （9): ∂h/∂我” = hf − h_我。However, we note that in our case, the system Hamiltonian can be parametrized by the alchemical weights, and ∂h_/∂我”can be calculated straightforwardly using automatic differentiation50on the MLIP.This method proves to be more efficient than linear interpolation as it obviates the need to repeat calculations for non-changing atoms.^{We compare computational efficiencies and the resultant free energy calculations inÂ} 补充信息。Free energy of vacancy formationAccurate evaluation of the free energy of a point defect is important for characterizing its thermodynamic stability

65

。^{Here, we calculate the Gibbs free energy of vacancy defined as}$${G}_{{{{\rm{v}}}}}={G}_{{{{\rm{defect}}}

在哪里g_缺点和g_完美的are the Gibbs free energies of crystal with and without a point defect, andnis the number of atoms in the perfect crystal.Because the vacancy diffuses at high temperatures, it is common to first evaluate the Gibbs free energies at low temperatures in which the vacancy is fixed at one site⁶⁶and extend the calculation by considering the temperature dependence of Gibbs free energy⁶⁷。Hence, we will focus on determining the Gibbs free energy of vacancy in BCC iron at low temperatures and compare the result with Gibbs free energies determined using the Frenkel–Ladd path⁶⁸, which is commonly used in nonequilibrium calculations^{33，，，，64}。In the Frenkel–Ladd path, the crystal structure is switched from and to a system of independent harmonic oscillators with the same equilibrium positions (the Einstein crystal), for which we can calculate the exact free energy.See Section “Free energy calculations” for more details on the reference calculation.

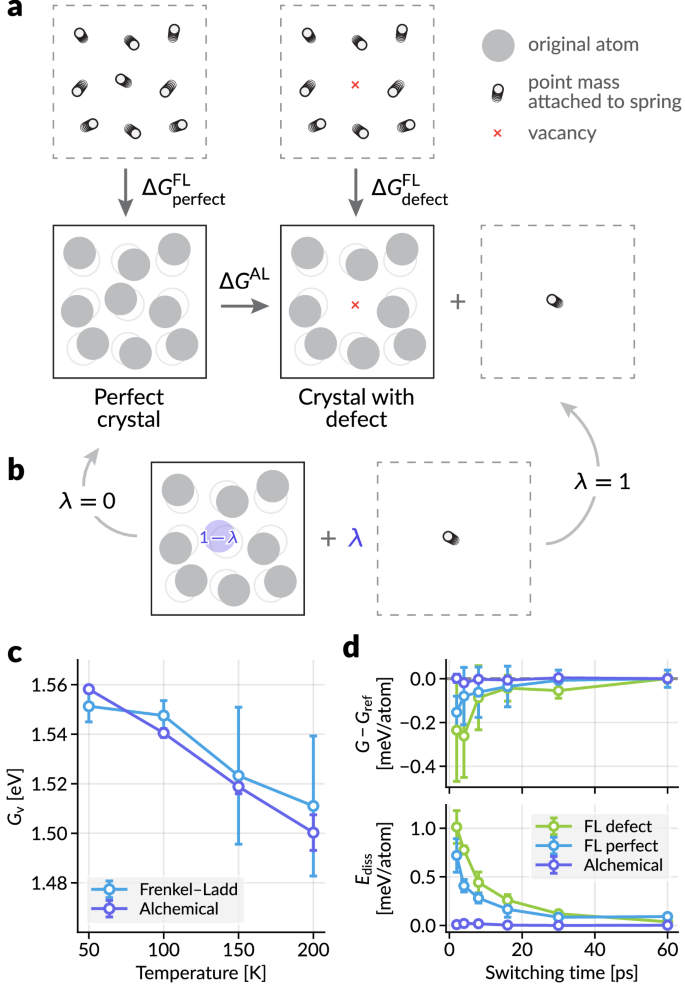
We introduce a new alchemical path for determining the free energy of vacancy, as depicted in Fig. 5一个。While the previous examples of our method were restricted to cases where\({\sum}_{\alpha }{\lambda }_{\alpha }=1\), we can lift this restriction to create or annihilate atoms in a system alchemically.In this case, we assign alchemical weight我”₁ = 1 − 我”to the atom in the vacancy site and switch the weight from 1 to 0 (我”from 0 to 1) over the simulation to make it continuously disappear from the system.At the same time, we add the harmonic oscillator term to the atom position with weight我”, so that through the alchemical conversion from我” = 0 to 1 transforms the perfect crystal into a crystal with defect and a harmonic oscillator (Fig. 5b）。Through nonequilibrium switching simulations, we can obtain the alchemical free energy difference Δg^al（等式（等式23）。We now compare the free energy of vacancy (Eq. (12)) obtained from both Frenkel–Ladd calculations (\({G}_{{{\rm{defect}}}}^{{{\rm{FL}}}}\)和\({G}_{{{\rm{perfect}}}}^{{{\rm{FL}}}}\)) and with alchemical free energy calculations (Δg^al和\({G}_{{{\rm{perfect}}}}^{{{\rm{FL}}}}\)）。

Transformations used to determine the Gibbs free energy of the perfect crystal and the crystal with a defect.The alchemical pathway used here transforms the perfect crystal into the crystal with a defect and a single atom attached to a spring to avoid diffusion.Δg佛罗里达州^{and Δ}gal^{represent the Gibbs free energy changes calculated via the Frenkel–Ladd and alchemical pathways, respectively.}bThe intermediate state parameterized by我”for the alchemical pathway in (一个）。The atom to be removed is assigned an alchemical weight of 1 − 我”, and the energy of the harmonic oscillator is scaled by我”。cThe free energy of vacancy (Eq. (12)) computed by the Frenkel–Ladd path and alchemical path.dStatistical efficiency for the Frenkel–Ladd paths and alchemical path at 100 K against the switching time.Upper panel shows the deviation of Gibbs free energy from the reference value at the longest switching time (60 ps), and the lower panel shows average dissipated energies (Eq. (10）。For panelsc和d, each data point represents the average of four statistically independent simulations, with standard deviations shown as error bars.Source data are provided as a Source Data file.

The results in Fig. 5c show thatg_vcalculated by the proposed alchemical free energy method is comparable to that from the reference Frenkel–Ladd calculations, while offering more consistent results with much smaller standard deviations when using the same switching time steps.We further investigate the statistical efficiency of the switching paths at 100 K by evaluating the convergence of Δg, taking the longest switching time result as its reference, as well as the dissipated energye_指责（等式（等式10)) in Fig. 5d。The alchemical pathway offers much faster convergence, with minimal average energy deviations ( < 0.02 meV/atom) from the reference value, even at a very short switching time of 2 ps (1000 MD steps).

Alchemical free energy calculations

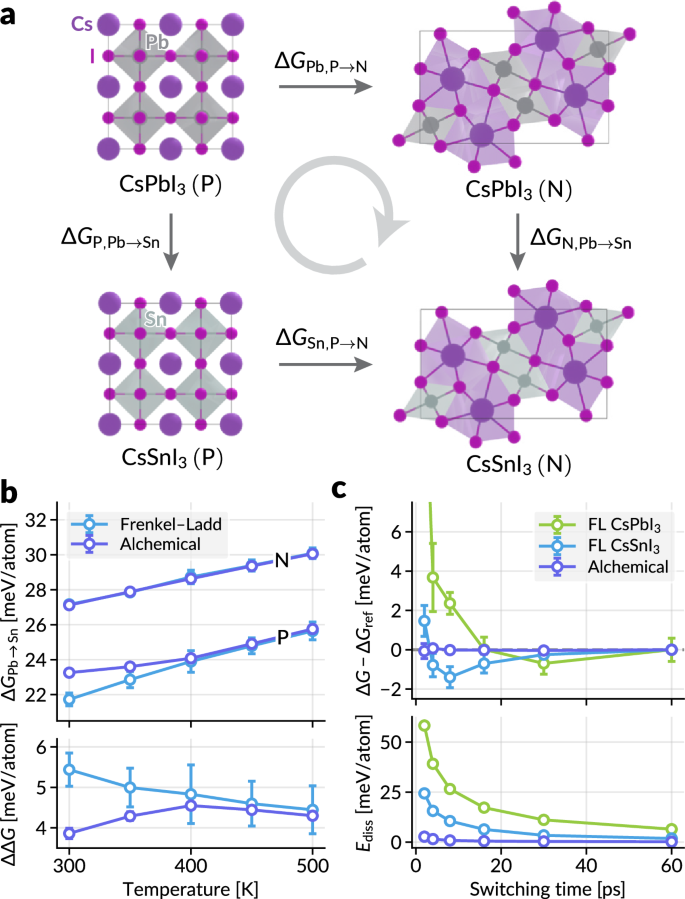
Now, we examine the effectiveness of the proposed alchemical scheme in the calculation of alchemical free energy difference associated with the change in the elemental identities of the atoms.We use halide perovskites CsPbI₃and CsSnI₃as our model system, which have been studied using MLIPs (e.g.,⁶⁹) and classical force fields (e.g.,^{70，，，，71}）。Both CsPbI₃and CsSnI₃exhibit three photoactive perovskite phases,α（立方体，\(Pm\overline{3}m\)），β(tetragonal,p4/mbm）， 和γ(orthorhombic,pnm一个), in decreasing order of temperature window of stability.However, they also possess a photoinactive non-perovskite polymorph,我(orthorhombic,pnm一个), which is the most stable phase at room temperature⁷²。Here, we analyze the difference in the relative stabilities of perovskite (P) and non-perovskite (N) phases as shown in the thermodynamic cycle in Fig. 6一个。The direct computation of the free energy of phase transformation, Δg_{Pb,P→N}and Δg_{Sn,P→N}, may require enhanced sampling simulations with tailored collective variables or nonequilibrium simulations (the Frenkel–Ladd paths) with longer simulation time until convergence.The alchemical path enables the calculation of Δg_{P,Pb→Sn}and Δg_{N,Pb→Sn}。Since the two types of free energy differences are linked by

we can compute the difference in the relative stability of phases upon compositional changes, or we can calculate either of the free energies of phase transformation if another is already known.

The thermodynamic cycle considered in this work, consisting of perovskite (P) and non-perovskite (N) phases of CsPbI3_{and CsSnI3}。_Δgvalues are labeled by phase (P or N) and composition;for instance, Δg_{N,Pb→Sn}indicates the gibbs free energy change for the non-perovskite phase from CsPbI₃to CsSnI₃。bUpper panel: the alchemical free energy of Pb→Sn conversion in both phases, plotted against the simulation temperature.Lower panel: the ΔΔgvalues in Eq.(13) computed from the results in the upper panel.The deviations between the two methods at lower temperatures result from the phase transformation between the perovskite phases.cStatistical efficiency for the Frenkel–Ladd paths and alchemical path of CsPbI3_{to CsSnI3}transformation for P phase, plotted against the switching time._{Upper panel shows the deviation of Gibbs free energy from the reference value at the longest switching time (60 ps), and the lower panel shows average dissipated energies (Eq. (}10）。For panelsb和c, each data point represents the average of four statistically independent simulations, with standard deviations shown as error bars.Source data are provided as a Source Data file.

For the alchemical free energy simulation, starting from the CsPbI₃structure, the Cs and I atoms remain as non-alchemical atoms, and the Pb atoms are divided into alchemical atoms, Pb and Sn, with alchemical weights我”₁ = 1 − 我”和我”₂ = 我”。Then, switching我”from 0 to 1 continuously transforms the CsPbI₃structure into the CsSnI₃结构。Refer to Section “Free energy calculations” for more details on the alchemical free energy calculation settings and result analysis required to obtain the Gibbs free energies.

First, we compare the Gibbs free energy of compositional change from two methods:\(\Delta {G}_{{{\rm{P}}}/{{\rm{N}}},{{\rm{Pb}}}\to {{\rm{Sn}}}}^{{{\rm{AL}}}}\)from the alchemical path and\(\Delta {G}_{{{\rm{P}}}/{{\rm{N}}},{{\rm{Pb}}}\to {{\rm{Sn}}}}^{{{{\rm{FL}}}}}={G}_{{{\rm{P}}}/{{\rm{N}}},{{\rm{Sn}}}}^{{{{\rm{FL}}}}}-{G}_{{{\rm{P}}}/{{\rm{N}}},{{\rm{Pb}}}}^{{{\rm{FL}}}}\)from the Frenkel–Ladd path for each composition.The results in Fig. 6b indicate that the two calculation results coincide well except for the slight deviation in the perovskite phase for temperatures lower than 400 K. The deviation may occur from the phase transformation between perovskite phases of CsPbI₃（IE。，α → β）。The Frenkel–Ladd path is simulated in the fixed cell (NVT) of the respectiveαphase, whereas the alchemical path is simulated in the NPT ensemble, in which phase transformations can occur.Given that theβphase is more stable than theαphase for CsPbI₃at low temperatures,\(\Delta {G}_{{{\rm{Pb}}}\to {{\rm{Sn}}}}^{{{\rm{AL}}}}\)is expected to be larger than\(\Delta {G}_{{{\rm{Pb}}}\to {{\rm{Sn}}}}^{{{\rm{FL}}}}\), as in Fig. 6b。See 补充信息 for further discussion.The calculation of ΔΔg（等式（等式13））还表明，这两个结果在较高的温度下匹配得很好，而炼金术路径则提供了与多个运行的较小标准偏差。

与上一个示例类似，我们分析了吉布斯自由能的收敛性和在400 K下钙钛矿相的炼金术路径的能量耗散，通过更改非平衡模拟的切换时间。Fig. 6c shows that, similar to the previous result, the alchemical path provides much faster convergence than the Frenkel–Ladd path.该结果证实，具有不同组合物的两个相同相结构之间的相空间重叠要比原子结构和爱因斯坦晶体之间的相重得多，这可以实现更有效的自由能模拟。

The alchemical modification of MLIP introduced in this work allows a smooth interpolation between structures with two or more different compositions.Building upon a prototypical construction of MLIP, we modified the input graph, message passing scheme, and readout layers to alchemically weight the different compositional states.Although this modification can be generalized to various classes of MLIPs, it is particularly efficient when integrated with MACE because of its construction of many-body features from two-body messages (see Section “Architecture-specific modifications”).

We first applied the scheme to the modeling of solid solutions.Although there is no theoretical relationship between the stoichiometry and the alchemical weights, the results showed that it could model the nonlinear deviations of cell parameters in some solid solutions.The end-to-end differentiability of the model with respect to the alchemical weights enabled the optimization of composition to match the desired cell parameters.The alchemical modification also provides a scalable, efficient method for characterizing order and disorder, as demonstrated in multicomponent perovskite oxides, achieving accuracy comparable to SQS with fewer number of atoms and no optimization needed for structure generation.Furthermore, the alchemical weights allow smooth creation or annihilation of atoms, or the change in atom types, enabling the calculation of free energy differences between two compositional states.We demonstrated that the free energy of vacancy in BCC iron and the relative phase stabilities of the perovskite and non-perovskite phases of CsPbI₃and CsSnI₃could be calculated much more efficiently than the widely utilized Frenkel–Ladd path.It is worth noting that, unlike the modeling of solid solutions, alchemical free energy calculations conducted here are theoretically exact when reaching convergence.

Overall, the proposed method enables efficient modeling of composition-related properties with sufficient consistency within the underlying MLIP.Beyond the aforementioned lack of theoretical ground on the connection between alchemical weights and stoichiometric coefficients and convergence questions that are universal to thermodynamic integration methods, inaccuracies emerge primarily from the MLIP.In particular, there are two sources of error: (1) the discrepancies between the MLIP and the DFT calculations and (2) the inaccuracy of the underlying DFT calculations.Since most universal MLIPs are trained on the energies and derivatives from the relaxation trajectory, the relative error around the energy minima would be small.This implies that the former error would also be small when performing free energy calculations for systems with a sufficient number of similar structures in the materials database.Fine-tuning the MLIP using the DFT data from relevant compositional space would alleviate the former error.One can also utilize free energy perturbation methods⁷³从更准确的哈密顿量计算自由能，以减少两种类型的错误。我们还注意到可区分的模拟^{74，，，，75}可以用来微调MLIP，以匹配由松弛轨迹引起的单元参数或从MD模拟到其所需值的自由能差，以减轻两个错误源。

While we devised the alchemical scheme with fixed elemental identities and我”representing the occupancies of different alchemical atoms to align with our goal of leveraging pre-trained MLIPs, we note that interpolating the elemental identities of atoms, i.e., coupling我”to atomic numbers, is also a promising direction that connects with the quantum alchemy literature.Although pre-trained embeddings may not be ideal for this, they could be fine-tuned by alchemical force matching with ∂e/∂我”derived from quantum alchemy^{22，，，，76，，，，77}, possibly using analytical gradients^{78，，，，79，，，，80}, given that the baseline MLIP is end-to-end differentiable with respect to embeddings.Learning an MLIP-based representation consistent with quantum alchemy might offer a well-regularized approximation of the physical state for the TI calculation.While this alternative scheme could improve the physical relevance of alchemical degrees of freedom, it is incompatible with the current approach and remains a prospect for future work.Beyond the applications demonstrated in this work, we expect that the gradient of the physical observables with respect to the composition or elemental identities would hold particular importance to the generative modeling of molecules and materials systems.We envisage that further works, integrated with the discrete sampling literature^{81，，，，82}，将在此类建模应用中利用MLIP中的自由度。

特定于架构的修改

在狼牙棒上，原子基础\({{{{\boldsymbol{A}}}}}_{i}^{(t)}\)通过将两体特征汇集在等式中的邻居上来构建。（（14）（等式（8）在原始论文中¹⁰）。在等式中传递消息的修改。（（6）通过乘以边缘的权重实现ω_αβ（等式（等式5））到等式中的消息汇总的汇总。（（15）：

原始读数机制是读出层的所有输出的站点能量的总和\({{{{\mathcal{R}}}}}_{t}(\cdot )\)（等式（等式16）。我们在等式中实现炼金术读数。（（7）作为等式中的炼金术点能量的加权总和。（（17）：

Representation of solid solution

We used the MACE-MP-0 medium model¹⁵for the experiments in Section “Representation of solid solution”.Fast Inertial Relaxation Engine (FIRE) algorithm⁸³, as implemented in the Atomic Simulation Environment (ASE) 3.22.1 package⁸⁴, was used to conduct geometry relaxations under fixed composition.

Compositional optimization

For the optimization for lattice-matching composition for solid solutions Al_1−xsc_xN and Al_1−xy_xN with GaN, we used∣σ_xx + σy_y∣as the optimization target to find the matching condition for cell parameter一个。We used gradient descent with learning rates 0.01 and 0.005 forcand alchemical weights我”， 分别。We initializedcwith the value from the optimized GaN structure and我”with [1, 0].The gradient of我”was projected onto the line我”₁ + 我”₂ = 1 by subtracting the mean value at each optimization step.

In general, when alchemical weights我”represent the compositional states, the weights should add up to 1 and the individual weights should be non-negative, i.e., the weights are element of the compositional simplex\({\Delta }^{k-1}=\{{{{\boldsymbol{\lambda }}}}\in {{\mathbb{R}}}^{k}\,| \,{\sum }_{\alpha=1}^{k}{\lambda }_{\alpha }=1,\,{\lambda }_{\alpha }\ge 0\}\)。We can perform gradient-based constrained optimization for the minimization target\({{{\mathcal{L}}}}({{{\boldsymbol{\lambda }}}})\)on the simplex by utilizing the exponentiated gradient descent method^{85，，，，86}with the update rule given as

在哪里我·is the learning rate.

Disordered energetics

We obtained 2 × 2 × 2 cation-ordered arrangements and experimental order/disorder label from the dataset reported in^{52，，，，53}on ordering of multicomponent perovskite oxides\({{{{\rm{A}}}}}_{2}{{{{\rm{B}}}}}^{{\prime} }{{{{\rm{B}}}}}^{{\prime}{\prime} }{{{{\rm{O}}}}}_{6}\)。We used the icet 3.0 package⁸⁷to optimize and generate 4 × 4 × 4 cation-disordered SQSs.Structural differences are identified by pooling localized fingerprints, generated usingOPSiteFingerprintfrom matminer 0.9.3⁸⁸, across all atoms to create crystal-level feature vectors^{53，，，，57}。The difference between two crystal features,x和y, is quantified as the cosine distance:d（（x，一个 y) = 1 − x⊤^y/（（∥x∥∥y∥）∈[0, 2].Free energy calculationsWe used the MACE-MP-0 small model15

for the experiments in Section “Representation of solid solution”.

MD integrations are performed with corresponding implementations in ASE⁸⁴, and a time step of 2 fs was used.^{The characteristic time scales of}Ï„t = 25 fs andÏ„_p = 75 fs were used for all the thermostats and barostats, respectively.Each simulation was initialized with energy minimization (with or without the cell fixed) using the FIRE algorithm₈₃and sampling the momenta from the Maxwell–Boltzmann distribution at the given temperature.^{The center of mass of the system was fixed for all MD simulations.}For all nonequilibrium simulations, we used the progress parameter scheduling of

在哪里τ = t/t_转变 ∈[0, 1] is the normalized switching time progress.Instead of linear我”（（Ï„) = τ, the scheme in Eq.（（19) was used because the slope d我”/dtvanishes at both ends and reduces the energy dissipation⁸⁹。All free energy calculation results were averaged over four statistically independent simulations, and their standard deviations are reported as error bars in Figs. 5和6。

Frenkel–Ladd path

Here, we adapted the procedure arranged in Menon et al.³³。First, the system was equilibrated for 60 ps under the NPT ensemble with the pressure ofp = 1 atm by the Berendsen thermostat and homogeneous Berendsen barostat90^。The average cell volume\(\left\langle V\right\rangle\)was calculated during the last 40 ps of the simulation.The spring constants for the Einstein crystal were estimated from the mean-squared displacement (MSD) of the atoms under the fixed system volume as\({k}_{i}=3{k}_{{{{\rm{B}}}}}T/\langle {(\Delta {{{{\boldsymbol{r}}}}}_{i})}^{2}\rangle\)⁶⁴。The fixed volume system was simulated for 100 ps under the NVT ensemble by the Langevin thermostat withγ = 1/Ï„_t⁹¹, and the MSD values were computed over the last 60 ps of the simulation.The MSD values were averaged and reassigned to the symmetrically equivalent atoms to reduce the variance before determining the spring constants.Finally, a nonequilibrium simulation of the Frenkel–Ladd path with the determined spring constants was conducted under the NVT ensemble using the Langevin thermostat.The system was equilibrated at我” = 0 for 40 ps, switched from我” = 0 to 1 with the schedule in Eq.（（19) for 60 ps, equilibrated again at我” = 1 for 40 ps, and switched back from我” = 1 to 0 for 60 ps.

The Helmholtz free energy for independent harmonic oscillators (Einstein crystal) with angular frequencies\({\omega }_{i}={({k}_{i}/{m}_{i})}^{1/2}\)is given as

Since the center of mass of the system is fixed, the following finite-size correction associated with the Frenkel–Ladd path was applied:

在哪里\({\mu }_{i}={m}_{i}/{\sum }_{i=1}^{N}{m}_{i}\)和n_WSis the number of Wigner–Seitz cells in the system^{92，，，，93}。Finally, the Gibbs free energy was determined as

where Δfwas calculated by Eq.（（11) from the nonequilibrium switching³³。

Free energy of vacancy

We used 5 × 5 × 5 supercell of BCC iron (250 atoms).The iron atom at the center of the supercell was removed to simulate the vacancy.We determined the spring constant from the NVT simulation of the perfect crystal and used the same spring constant for both Frenkel–Ladd paths of the perfect crystal and the crystal with vacancy and for the alchemical pathway of switching the atom into a spring.All NPT simulations were conducted under a pressure of 1 atm.Before the alchemical switching process, the initial system was equilibrated for 20 ps using the Berendsen thermostat and barostat (inhomogeneous) to reduce initial fluctuations in the cell volume.Then, the Nose–Hoover and Parrinello–Rahman dynamics⁹⁴were used to simulate the switching process.相同我”scheduling for the Frenkel–Ladd path was used, with equilibration and switching times of 40 ps and 60 ps, respectively.The alchemical free energy change Δg^alwas determined using Eq.（（11), and satisfy the following relationship:

where the free energy of springf_春天could be computed from Eq.（（20） 和n = 1.

Alchemical free energy calculations

We started from 6 × 6 × 6 supercell ofα-CsPbI₃for perovskite phase and 6 × 3 × 3 supercell of我-CsPbI₃for non-perovskite phase.Both systems contain 1080 atoms.For the alchemical pathway, we used the same simulation procedure as the alchemical pathway for the vacancy, under a pressure of 1 atm.Additionally, we set the masses of atoms as the weighted sum of masses of alchemical atoms, i.e.,\({m}_{i}(\lambda )=(1-\lambda ){m}_{i}^{({{\rm{i}}})}+\lambda {m}_{i}^{({{\rm{f}}})}\), through the switching process.The alchemical free energy change was computed as

where Δgis computed using Eq.（（11）。The second term on the right-hand side accounts for the change in masses over the transformation and originates from kinetic energy contributions³³。

报告摘要

Further information on research design is available in the Nature Portfolio Reporting Summarylinked to this article.

https://github.com/learningmatter-mit/alchemical-mlip95。^参考Marx, D. & Hutter, J.

作者和隶属关系

1. Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA

   Juno Nam, Jiayu Peng & Rafael Gómez-Bombarelli

贡献

J.N.and R.G-B.conceived the project.J.N. designed the methodologies and developed the algorithms.J.N.and J.P. implemented the code and analyzed the results.R.G-B.监督研究。All authors discussed the results and contributed to the final manuscript.

相应的作者

对应Rafael Gómez-Bombarelli。

竞争利益

作者没有宣称没有竞争利益。

同行评审信息

自然通讯thanks the anonymous reviewer(s) for their contribution to the peer review of this work.提供同行评审文件。

开放访问本文允许以任何媒介或格式的使用，共享，适应，分发和复制允许使用，分享，适应，分发和复制的国际许可，只要您适当地归功于原始作者和来源，就可以提供与创意共享许可证的链接，并指出是否进行了更改。The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.To view a copy of this licence, visithttp://creativecommons.org/licenses/4.0/。重印和权限

About this article