A thermodynamic inspired AI based search algorithm for solving ordinary differential equations

Mathematical modeling in most scientific and engineering areas is revolving around Ordinary Differential Equations (ODEs). In subjects like physics, chemistry, biology, finance and control systems, they have been extensively used to characterize dynamic evolution of systems. These characterize the rate at which a dependent variable change with respect to an independent variable and describe the dynamics of a system. They are used to describe Newtonian mechanics, chemical reaction kinetics, and epidemiological models^1,2,3, as well as to describe electrical circuits³.

However, despite their ubiquity and importance, finding the closed form analytical solutions for ODEs is usually not practical, especially when the ODEs are nonlinear, coupled, or of high orders. The complexity occurring is very common as it pops up when turbulence modeling, biochemical reaction network, or chaotic systems appear in real-world modeling⁴. Therefore, numerical methods to approximate ODEs are nowadays indispensable. Many classical numerical methods are found in practice^5,6,7 such as Euler’s method, Runge–Kutta methods and finite difference methods (FDM). These methods consist of discretizing the domain and propagating the solution iteratively in time over the mesh points. These methods work well with simple and well posed problems but can suffer many deficiencies in highly nonlinear and/or stiff systems or boundary value problems on irregular domains⁸. Most of these algorithms are compromised in accuracy and robustness by error propagation, grid dependence and computational instability⁹.

Due to the drawback of grid based numerical methods, mesh free approaches present themselves as viable alternatives. Radial basis function (RBF) interpolation, finite point methods, as well as element free Galerkin methods, have achieved significant popularity recently because the resulting methods are free from meshing and grid distortion¹⁰. The former make use of scattered points in the domain instead of structured grids, which provide more flexibility and decrease error accumulation¹¹. Mesh free methods are however very sensitive to the choice of basis functions and the definition of its parameters which need to be fine-tuned by sophisticated optimization techniques¹².

The past decade has witnessed the increase in the use of metaheuristic optimization algorithms to solve ODEs by posing the problems as an optimization problem. Therefore, in this context, the ODEs are reformulated in order to minimize the residual error between the approximate and exact solutions through the means of optimization strategies. Some of the metaheuristics suggested for learning linear and nonlinear ODEs are Differential Evolution (DE)¹³, Particle Swarm Optimization (PSO)¹⁴, Genetic Algorithms (GA)¹⁵, Artificial Bee Colony (ABC)¹⁶, and Water Cycle Algorithm (WCA¹⁷). Although various metaheuristic algorithms such as Differential Evolution (DE), Particle Swarm Optimization (PSO), Genetic Algorithms (GA), Artificial Bee Colony (ABC) and Water Cycle Algorithm (WCA) are widely equipped, each of them has weaknesses to solve Ordinary Differential Equations (ODEs), and there may exist some methodologies to overcome these difficulties:

• Differential Evolution (DE): DE is a population-based algorithm, which utilizes the characteristic of optimum in a complex objective function. However, it faces premature convergence problem, especially when search space dimensionality is high, it easily gets stuck in local optima. Additionally, the scaling factor and mutation parameters of DE are sensitive, requiring tuning when solving ODEs with different characteristics.

• Particle Swarm Optimization (PSO) is a candidate optimization algorithm which is inspired by the social behavior of particles to search solution space. PSO is, however, effective only in global search but prone to stagnation convergence in dealing with complex or very high nonlinear ODEs. Moreover, it struggles to keep diversity in the population in the later stages of optimization which often implies insufficient exploration of the solution space and poor performance on high dimensional problems.

• Genetic Algorithms (GA) work with principles of natural selection and is famous for it flexibility. Nevertheless, solving the ODE has a problem of slow convergence of GA and especially when dealing with stiff or chaotic systems. It also calls for an appropriate trade off in crossover and mutation rates and its search process is usually not as efficient as other approaches in managing the large and dynamic solution space of ODEs.

• Artificial Bee Colony (ABC) is based on the foraging behavior of honeybees and is also applied to solve the ODE in the literature yet commonly suffers from the problem of premature convergence and insufficient exploration. Despite its adaptiveness, there may be limitations in its search behavior to satisfy high dimensional ODE systems, and therefore, suboptimal accuracy is found when dealing with complex problems.

• Water Cycle Algorithm (WCA): WCA, based on the natural process of water cycle, has also been indicated to be successful on optimization tasks. Yet, it is highly sensitive to parameter settings and thereby can be inconsistent in ODE solving. Moreover, slow convergence of WCA is an issue in the presence of large search space or highly nonlinearity.

The weight of these weaknesses may be greatly increased in problems involving ODEs, where it is an essential endeavor to find a balance between global exploration and local exploitation, particularly for nonlinear, coupled, or high-dimensional systems. This paper introduces Thermodynamic-Inspired Search Algorithm (TSA) to overcome these issues by incorporating energy minimization, heat exchange and entropy control into its underlying search, which improves exploration, exploitation, and robustness in solving ODEs.

The first advantage of these algorithms is that they are able to perform on objective functions that are not differentiable, or which possess local optima and are able to adapt to a complex problem landscape. Yet, they do not lack challenges. Nevertheless, many metaheuristic algorithms are mostly faced with the drawbacks like premature convergence, slow exploration in high-dimensional search space, sensitivity in parameter setting¹⁸.

It has been observed that Differential Evolution (DE) and its adaptive versions, SHADE and L-SHADE are particularly suitable methods to solve the ODEs thanks to their capability to optimize the right tradeoff between exploration and exploitation¹⁹. These methods, when coupled to Fourier periodic expansion functions and weighted residual techniques, have proven very accurate and faster converging to machine accuracy²⁰. A flexible functional form for approximating solutions is provided by Fourier series representation and weighted residual techniques then minimize the deviation between the trial solution and the exact solution over the domain²¹.

Nevertheless, there is still a need to find a metaheuristic algorithm that is both adaptive and robust, and which can efficiently and consistently solve the ODE. This paper introduces a new Thermodynamic-Inspired Search Algorithm (TSA) inspired by the laws of thermodynamics. The rationale of the algorithm integrates the ideas of energy minimization, heat exchange, and entropy regulation into the search procedure. In physical systems, particles like to move to states of lower energy and have an equilibrium when all the energy is spread in an equal manner. TSA carries out global exploration and local exploitation on the fly by simulating thermodynamic processes. Entropy is used as a measure of population diversity in order to prevent the algorithm from converging too early and to guarantee more search of the solution space. An annealing schedule gradually controlling focus of search by moving it from exploration to exploitation accelerates convergence.

The proposed TSA is coupled with Fourier periodic expansion and a least-square weighted residual to form a mesh-free ODE solver. Through the combination of these techniques, TSA achieves the capability of approximating solutions to LODEs and is also successful in solving NLODEs and SODEs. Experiments on a benchmark suite of twenty ODEs show that TSA is consistently more accurate, converges faster, and is more robust than state of the art techniques, that is ADE PSO and ABC.

First, this paper is organized as follows. In the second section the existing literature on the classical numerical methods, meshfree methodologies and metaheuristics algorithms used to solve the initial value problems of Ordinary Differential Equations (ODEs) is reviewed. In Section" Proposed Thermodynamic-Inspired Search Algorithm (TSA)", the Thermodynamic Inspired Search Algorithm (TSA) is formulated based on the working principles of the proposed algorithm. The application of TSA to ODEs is explained in the following section, particularly Fourier periodic expansion and the weighted residual minimization technique. The experimental setup is outlined in Section"Experimental Setup", in terms of benchmark problems, performance criteria and related comparison algorithms. Comparison of experimental results are presented in Section"Results and Discussion". Section"Conclusion and Future Work"discusses complexity analysis and the special benefits of TSA. Finally, Sect.  8 concludes the paper and further suggests future directions of research.

The numerical solution of Ordinary Differential Equations (ODEs) has been a longstanding research focus in computational mathematics and engineering. Over the past decades, numerous methodologies have been developed, ranging from classical numerical integration schemes to modern mesh-free approaches and metaheuristic algorithms. In recent years, hybrid techniques combining basis functions and optimization strategies have also demonstrated considerable success. This section reviews the development and progress in each of these categories.

Classical numerical methods

Euler’s method and the Runge–Kutta family of methods are still revered among classical numerical methods in the field of ODEs²². They are based on discretization of problem domain done in small intervals and iterative approximation of the solution.

The simplest numerical technique using first order approximation is Euler’s method:

where \(h\) is the step size, and \(f\left( {x,y} \right)\) is the given function representing the ODE.

Euler’s method is easy to implement, but it has low accuracy and is unstable. However, to abolish these limitations, higher order methods (i.e. classical fourth order Runge–Kutta (RK4) method²³,) were introduced.

where

Despite their good behavior in non-stiff problems, these classical techniques become inefficient for stiff and highly nonlinear ODEs²⁴. In addition, they are mesh dependent and so are not easily extended to complex systems.

Mesh-free methods

Grid based approaches are substituted by other mesh free methods that represent the solution using a set of scattered nodes in the domain²⁵. While these methods are effective for problems of irregular geometries and dynamically changing domains, they have not yet been shown able to perform large scale optimization problems.

The Radial Basis Function (RBF) method is a well-known meshfree approximation that approximates the solution as:

where \(\phi \left( . \right)\) is a radial basis function, \(x_{i}\) are the scattered points, and \(\lambda_{i}\) are unknown coefficients to be determined²⁶.

Another important technique is the Element-Free Galerkin (EFG) method, which employs moving least squares (MLS) shape functions to approximate the solution:

where \(p_{i} \left( x \right)\) are polynomial basis functions, and \(a_{i} \left( x \right)\) are coefficients determined by minimizing a weighted least-squares error over neighboring points²⁷.

However, in some cases, mesh free methods are highly flexible and accurate, but at the same time, both tuning of appropriate parameters and computational cost can be problematic²⁸.

Metaheuristic optimization algorithms

Metaheuristic algorithms appear as strong methods to address ODEs because they change the differential equation into an optimization problem structure. The objective of this method consists in achieving minimum error discrepancy between the trial solution and the exact solution^29,30.

Differential Evolution (DE) stands as one of the most adopted metaheuristics that specializes in complex systems. The trial solution generated takes the following form:

where \(x_{r1}\), \(x_{r2}\),\(x_{r3}\) are randomly chosen individuals, and \(F\) is the scaling factor³¹.

The algorithm of Particle Swarm Optimization (PSO) duplicates natural social behavior among particles to tackle ODEs excellently. Each particle updates its velocity and position through the following procession:

where \(\omega\) is the inertia weight, \(c_{1}\), \(c_{2}\) are acceleration coefficient, \(r_{1}\), \(r_{2}\) are random values in \(\left[ {0,\;1} \right]\) \(p_{i}\) is the particle’s best position, and \(p_{g}\) is the global best position³².

Nonlinear ODEs present no challenge for these flexible methods yet these methods come with the drawbacks of demanding computation and risk of quick convergence termination³³.

Hybrid approaches

The combination of basis functions with residual minimization along with metaheuristic optimization techniques demonstrates excellent prospects for solving ODEs. The Fourier series serves as a common basis function for periodic system applications³⁴:

where \(L\) is the period, and \(a_{m}\),\(b_{m}\) are coefficients optimized using metaheuristics³⁵.

Several scientists utilize weighted residual methods specifically the least-squares weighted residual approach to minimize total domain error³⁶. The incorporation of hybrid techniques links metaheuristic global search capacities to basis function smoothness and produces accurate stable solutions³⁷.

As a new metaheuristic optimization algorithm³⁸ TSA operates to solve complicated optimization problems that include Ordinary Differential Equations (ODEs). TSA receives its foundation from observing how particles react to thermodynamic systems through their process of heat dissipation and energy exchange and their entropy regulation capabilities. The thermodynamic principles create a natural approach for managing the ideal relationship between exploration and exploitative operations throughout the solution domain.

Algorithmic inspiration

The Transportation Security Administration operates based on fundamental thermodynamic principles. Particles throughout physical systems naturally move towards less energetic stable states to settle at thermal equilibrium conditions. The First Law of Thermodynamics explains energy conservation yet the Second Law of Thermodynamics shows how entropy (disorder) rises progressively with time. The optimization targets align with these principles because they aim to minimize objective function (energy) alongside maintaining diverse (entropy) population elements for prevention of local optima³⁹.

Key thermodynamic concepts incorporated into TSA include:

• Energy Minimization: Better solutions correspond to lower energy states.

• Heat Exchange: Particles interact with each other, exchanging energy based on their relative fitness levels.

• Entropy Control: Diversity is maintained to prevent premature convergence.

• Temperature Annealing: Temperature controls the balance between exploration and exploitation; it decreases over time to refine the search near optimal solutions.

The search behavior of TSA is adaptively regulated by temperature and entropy, allowing it to efficiently explore the solution space early on and concentrate on promising regions in later stages⁴⁰. The combination of these mechanisms ensures that TSA can handle complex, high-dimensional search spaces more effectively than traditional metaheuristics⁴¹.

Pseudocode for thermodynamic-inspired search algorithm (TSA)

The Thermodynamic-Inspired Search Algorithm (TSA) is built upon thermodynamic principles, incorporating concepts such as energy minimization, heat exchange, and entropy control. TSA utilizes these principles to guide the search process, balancing exploration and exploitation effectively. The following pseudocode outlines the step-by-step execution of TSA.

1. 1.

   Initialize population P of size N randomly within the feasible solution space

2. 2.

   Evaluate the fitness of each particle in the population

3. 3.

   Assign initial energy levels to each particle based on their fitness

4. 4.

   Set initial temperature T and cooling rate α (0 < α < 1)

5. 5.

   While termination criteria not met (e.g., maximum iterations or convergence tolerance):

a. For each particle i in population P:

1. i.

   Perform energy exchange with other particles based on relative fitness

2. ii.

   Update the position of particle i based on energy exchange and temperature

3. iii.

   Calculate the new fitness of particle i

4. iv.

   Update energy level of particle i based on new fitness

5. v.

   Update entropy of the population to measure diversity

6. vi.

   Apply entropy control if necessary to maintain diversity (avoid premature convergence)

b. Update temperature T using an exponential decay:

T = T * α

1. 6.

   Return the best solution found by the population as the final solution

2. 7.

   End

Explanation of TSA pseudocode

• Step 1: Population initialization:

The algorithm begins by initializing a population of candidate solutions, with each solution represented as a particle. These particles are placed randomly in the solution space.

• Step 2: Fitness evaluation:

Each particle’s fitness is evaluated based on the problem’s objective function, and the fitness values are used to calculate the energy levels of the particles.

• Step 3: Energy exchange:

Particles with better fitness levels interact with other particles, sharing energy and guiding the population towards optimal regions of the solution space.

• Step 4: Temperature and cooling:

The temperature starts high and gradually decreases over time, promoting exploration at the beginning and exploitation at later stages. The cooling rate is controlled by the parameter α.

• Step 5: Entropy control:

Entropy is used to measure the diversity of the population. If the population converges too quickly, entropy control mechanisms are applied to prevent premature convergence and encourage further exploration.

• Step 6: Convergence and solution:

The algorithm continues until the stopping criteria are met, at which point the best solution found is returned.

Thermodynamic principles and ODE solving

Using the mapping between the thermodynamic principles and the optimization landscape of solving Ordinary Differential Equations (ODEs), the ability to explore and exploit between information necessary to achieve optimal solutions defines the task at hand. For this, the thermodynamic principles are particularly proven because they model the behavior of the physical systems in the same way in which we want to solve the ODEs, especially in complex and in non-linear or stiffness cases where the traditional methods are a problem.

1. i.

   Energy minimization: In systems where thermodynamics are involved, particles should fall from higher energy states to lower energy states and stop at the point of equilibrium (equilibrium being the lowest energy state). Thus, from this principle, TSA guides the search toward more optimal solutions and avoids suboptimal ones.

2. ii.

   Heat exchange: Energy is transferred between particles of thermodynamic systems in order to create uniform energy distribution. For instance, like TSA, in FDI search agents exchange energy based on their fitness values so as to enhance collaboration in the search. This heat exchange helps TSA to avoid premature convergence and to increase the diversity by making the particles with better solutions to impact other particles to explore more.

3. iii.

   Entropy control: Entropy is the measure of a tendency to disorder or randomness of a system, in thermodynamics. Entropy control maintains population diversity during optimization when it is carried out by the TSA. When entropy falls too low (showing premature convergence), TSA modifies exploration strategy to avoid being stuck at local minima, causing the robustness as well as global search ability of the algorithm to increase.

These principles help TSA avoid issues common in traditional methods, such as grid dependency, error propagation, and poor convergence in complex ODE problems. The combination of energy-driven movement, entropy-based diversity control, and temperature annealing provides TSA with a robust and adaptive search process that performs well even in challenging ODE-solving scenarios.

Fourier-based methods and their limitations

For the solution of Ordinary Differential Equations (ODE) possessing periodic or smooth behaviors, Fourier periodic expansions are commonly used. Fourier methods represent the solution as a sum of sine and cosine functions, in order to efficiently approximate periodic solutions. However, they assume that the solution is periodic and smooth, which do not apply readily to ODEs with discontinuities or non-periodic behavior.

1. i.

   Limitations in handling discontinuities. However, Fourier based methods inherently fail when used on ODEs with discontinuities. Since Fourier expansions are based on the fact that the solution is continuous, they are not able to represent solutions with sharp transition or sudden changes. In the same situations, there may be oscillations in the Fourier series near the points of discontinuity (The Gibbs phenomenon). The net effect of these oscillations is to obtain an incorrect representation of the solution, in particular near discontinuity points. For those ODEs with sudden changes, therefore, the Fourier method probably is not the best approximation to proceed to find a solution, because it is not found a good way to represent such sharp features.

2. ii.

   Challenges for non-periodic ODEs. This means that the solution of the ODE will not be periodic in general, and so the Fourier series is not well suited for such ODEs. In problems where the solution does not repeat in a regular or localized fashion, Fourier expansions may not give a good approximation. For this reason, Fourier methods are not particularly good for approximating non periodic solutions, since the basis functions (sines and cosines) are designed to approximate periodic phenomena. Such a mismatch can lead to important errors in ODEs where the solution behavior is more intricate and cannot be represented by periodic functions.

3. iii.

   Alternative approaches to overcome fourier limitations. Several alternative approaches for the discontinuous or otherwise non-periodic ODEs will be explored to address the limitations of the Fourier based methods:

   • Piecewise approximation: Piecewise approximations by splines or other piecewise smooth functions are an effective way of representing the solution to ODEs with discontinuities for regions of discontinuity in which the solution is continuous or otherwise can be well approximated by polynomials. The reason that this approach is particularly useful is that when the problem decays abruptly, it more accurately represents things than Fourier expansions.

   • Wavelet transforms: Wavelet transforms are very promising alternative when ODEs have non periodical behavior. Wavelets are different from Fourier methods in that the latter are based on global basis functions (sine and cosine) while the wavelets have a local multi resolution approach that can best fit to changes in the solution at a variety of scales. Wavelet based methods allow us to analyze high frequency as well as low frequency components of the solution which makes them more appropriate for capturing non periodic, rather irregular behavior of ODEs.

   • Finite element methods (FEM): Another alternative is provided by Finite Element Methods, particularly for ODEs having discontinuities or coefficients that depend on geometry. FEM approximates the solution using simpler functions in each element (subdomains of solution domain) and dividing solution domain into small subdomains (elements). For problems with sharp transitions or non-smooth behavior this method is very effective as it permits us to perform localized approximation and in so doing produce a higher accuracy in places where the solution changes sharply.

Initialization

The TSA begins with an initialization phase that ensures diversity in the solution space, setting the stage for an efficient search process.

Population initialization

Let the optimization problem be expressed as:

where \(f:R^{D} \to R\) represents the objective function, and \(x\) is s \(D\)-dimensional vector within the feasible region \(\Omega\).

The initial population of \(N\) particles is randomly generated as:

where \(x_{\min }\) and \(x_{\max }\) are the lower and upper bounds of the search space, \(r_{i} \approx U\left( {0,1} \right)\), and \(\Theta\) denotes the element-wise product.

Energy assignment

Each particle is assigned an initial energy proportional to its objective function value:

where \(\alpha> 0\) is a scaling constant.

Initial temperature

The initial temperature \(T_{0}\) is defined based on the standard derivation of the energy levels:

where \(k> 0\) is a user-defined constant, and

Entropy initialization

Entropy quantifies the diversity of the population:

with selection probability:

Energy exchange and solution update

Once initialized, the population evolves iteratively by updating particle positions based on energy exchange, temperature adjustments, and entropy evaluation.

Temperature annealing

Temperature \(T\left( t \right)\) is reduced using an exponential decay schedule:

where \(\beta> 0\) is the cooling rate, and \(t\) is the iteration number⁴².

Entropy update

Entropy at iteration \(t\) is updated as:

where:

Position update

Particles move towards low-energy states influenced by neighbors:

where

with energy difference \(\Delta E_{ij} = E_{j} - E_{i}\).

Acceptance criterion

The acceptance of a new position is determined by:

where \(\Delta E_{i} = f\left( {x_{i}^{t + 1} } \right) - f\left( {x_{i}^{t} } \right)\).

These rules ensure particles gradually converge to the global minimum while maintaining diversity in the early stages⁴³.

Entropy-based diversity control

Diversity control is crucial in population-based optimization algorithms to prevent premature convergence and ensure comprehensive exploration of the search space. In TSA, entropy is utilized as a measure of population diversity. Inspired by the concept of entropy in statistical thermodynamics, diversity is treated as the degree of disorder among particles in the population⁴⁴.

Entropy is defined as:

where:

• \(S\left( t \right)\) is the entropy of the population at iteration \(t\).

• \(p_{i}^{(t)}\) is the probability of selecting particle \(i\) based on its energy level:

  $$p_{i}^{(t)} = \frac{{{\raise0.7ex\hbox{${e^{{ - E_{i}^{(t)} }} }$} \!\mathord{\left/ {\vphantom {{e^{{ - E_{i}^{(t)} }} } {T(t)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T(t)}$}}}}{{\sum\nolimits_{j = 1}^{N} {{\raise0.7ex\hbox{${e^{{ - E_{i}^{(t)} }} }$} \!\mathord{\left/ {\vphantom {{e^{{ - E_{i}^{(t)} }} } {T(t)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T(t)}$}}} }}$$

  (24)

where \(E_{i}^{(t)}\)is the energy level of particle \(i\)and \(T\left( t \right)\) is the system temperature at iteration \(t\).

Adaptive entropy control mechanism

High entropy reflects a diverse population, indicating that the particles are exploring different regions. Low entropy suggests that particles are clustered around specific areas, potentially leading to premature convergence. TSA employs an adaptive entropy threshold to regulate diversity during the search process⁴⁵:

where \(\delta_{S}\) is the normalized entropy, and \(S_{\max }\) is the maximum theoretical entropy given by:

where \(\delta_{S} < \varepsilon_{low}\), diversity is deemed insufficient, and perturbation is applied to randomly relocate a fraction of particles to new positions.

where \(r_{i} \approx U\left( {0,1} \right)\).

If \(\delta_{S}> \varepsilon_{high} ,\) the population is considered highly scattered, and exploitation is emphasized by biasing particle movement toward the global best particle:

where \(\lambda \in \left( {0,1} \right)\) is a learning rate, and \(x_{g}^{t}\) is the best solution found so far.

Typical values are \(\varepsilon_{low} = 0.2\) and \(\varepsilon_{high} = 0.9\)⁴⁶.

Entropy-based diversity control prevents premature convergence, enabling TSA to maintain exploration capabilities throughout the optimization process⁴⁷.

Temperature reduction (annealing process)

Temperature control is a distinguishing feature of TSA, governing the transition from global exploration to local exploitation. The temperature reduction strategy is inspired by the annealing process in thermodynamics, where a material is gradually cooled to achieve a low-energy crystalline structure.

Exponential cooling schedule

The most commonly employed temperature reduction scheme in TSA is the exponential decay schedule⁴⁸:

where:

• \(T_{0}\) is the initial temperature.

• \(\beta> 0\) is the cooling rate.

• \(t\) is the iteration number

Exponential cooling is simple and widely used; however, it may lead to premature convergence if the cooling rate is too high⁴⁹.

Adaptive cooling schedule

To address the limitations of fixed-rate cooling, TSA incorporates an adaptive cooling scheme based on population entropy. When entropy is low (indicating convergence), temperature reduction is slowed to enhance local exploitation. Conversely, when entropy is high, temperature is reduced more rapidly to encourage exploration⁵⁰:

• \(\eta \varepsilon \left( {0,1} \right)\) is a cooling adjustment parameter.

• \(\delta_{s}^{t\arg et}\) is the desired entropy level.

Adaptive cooling aligns the temperature reduction rate with the population’s diversity, dynamically balancing exploration and exploitation⁵¹.

Stopping criteria

An effective stopping criterion is essential to terminate the optimization process when the algorithm has sufficiently converged, preventing unnecessary computations. TSA incorporates multiple stopping conditions to ensure reliability across different problem types.

Maximum iterations

The algorithm terminates after a predefined number of iterations:

Convergence tolerance

The algorithm declares convergence when the threshold gap between optimal fitness values and average fitness values is reached:

where:

• \(f_{best}\) is the best objective value.

• \(f_{avg}\) is the average objective value of the population.

• \(\varepsilon \,f\) is a user-defined convergence threshold.

Temperature threshold

The procedure ends when temperature drops below its set minimum point:

where \(T_{\min }\) is a user-defined minimum temperature.

By utilizing these criteria TSA maintains robust performance across different problem areas which leads to solution quality assurance and avoids premature termination⁵².

Computational complexity of TSA

The computational complexity of the Thermodynamic-Inspired Search Algorithm (TSA) on the number of particles (population size) and the number of iterations is determined mostly by. Also, like other population-based metaheuristic algorithms, TSA can be of complexity order O(N × T) where N pertains to population size and T to the number of iterations. This implies the total time of iteration required for the TSA to compute and update the positions of all particles.

However, they contain further computational steps because of their thermodynamic principle and hence marginally complicating it compared to conventional evolutionary techniques. These processes constitute the additional processes of TSA:

• Energy exchange: In addition, each particle interacts with others with respect to their relative fitness, they share part of their energy, which involves another computational cost per iteration.

• Entropy control: The diversity is measured in terms of entropy of the population, by involving additional calculations to avoid premature convergence. As a consequence, it leads to a higher per iteration computational load.

Although they may introduce extra steps to compute the balance of exploration and exploitation, both energy minimization and entropy control led to more efficient convergence in many of the cases. The fewer iterations in turn often offset the cost of additional computational time consumed for entropy control and energy exchange.

In comparison with other state of the art metaheuristic, Particle Swarm Optimization (PSO), Genetic Algorithms (GA), Differential Evolution (DE), and Artificial Bee Colony (ABC), TSA has also the time complexity of O(N × T). Nevertheless, by using thermodynamic principles as used by TSA, faster convergence and lower number of iterations often imply lower total computational cost in realistic applications.

Briefly, the notions of entropy and energy computation slightly increase TSA’s computational complexity, however, efficient exploration and exploitation mechanisms again result with better performance and reduced iteration that make TSA competitive in terms of overall computational efficiency, compared to conventional metaheuristics.

Sensitivity analysis of TSA hyperparameters

Many TSA’s hyperparameters, including temperature decay rate, entropy thresholds, as well as energy scaling, are seen to greatly impact the performance of TSA. Each of these parameters is important in determining how quickly the algorithm converges to high quality and easily found values for each design variable. A comprehensive sensitivity analysis is done to figure out which of these hyperparameters are important to TSA’s performance. In this section, we report the findings of this analysis and what is the optimal setting of each hyperparameter along with their combined impact on TSA’s overall performance.

Temperature decay rate (α)

However, the rate of temperature decay (indicating how rapidly the temperature decreases from the execution of TSA) is determined by the temperature decay rate (denoted by α). A faster decay rate results in a higher temperature for a shorter time, encouraging more exploitation, and a slower one keeps the temperature high for longer time, and therefore more exploration of the solution space.

• Effect on performance: From the sensitivity analysis, it can be found that the decay rate α must be slowed down to allow more thorough exploration, but with the associated drawback that the computational time will be increased. In contrast, a slower decay rate (higher values of α) leads to quicker convergence (sooner), but the algorithm does converge too soon to something that is suboptimal.

• Optimal range: Furthermore, it was found that the optimal temperature decay rate lies between 0.85 and 0.95. Bounded close to this range, TSA was able to balance exploration and exploitation in a reasonably efficient manner without using excessive computational overhead as it converged to a solution.

Entropy thresholds (ET)

A critical parameter for the diversity of the population is the entropy threshold (ET). However, in exploration, high entropy thresholds lead to a more diverse population by encouraging exploration of new areas of solution space and help in convergence by imposing low entropy thresholds that lead to restricted search to a smaller neighborhood of solution space.

• Effect on performance: At high threshold a high entropy the algorithm converges too slowly because of excessive exploration and equiprobability structure become inefficient. In contrary, a low entropy threshold results in a faster speed of convergence but faces a tendency to be stuck to local optima due to insufficient exploration.

• Optimal range: We analyzed entropy thresholds within the range of 0.4 to 0.6 as the best. Within this range, it maintained a sufficient level of population diversity for TSA to explore new areas before converging in a reasonable amount of time.

Energy scaling factor (ESF)

The energy scaling factor (ESF) controls the amount of energy that is exchanged between particles in the population and corresponds to the coefficient in the expression relating moves from the supplier to moves from the buyer. A larger scaling factor creates greater effect of the fittest particles, which for quicker convergence, but a modest scaling factor brings out balanced energy dissemination between particles for exploration.

• Effect on performance: Based on the results of the sensitivity analysis, we find that high energy scaling factors cause TSA to converge more quickly but might also lead to earlier exploitation of suboptimal solutions. On the other hand, low energy is sampling the larger search space but at the slower convergence.

• Optimal range: It was found that the moderate energy scaling factor in the range 0.6 to 1.0 gave the optimal performance. This range of values enabled TSA to adjust convergence speed and exploration to achieve fast and quality solutions, provided with adequate diversity.

Combined effect of hyperparameters

An assessment was made to the sensitivity of each individual hyperparameter as well as the overall combined effect of all three parameters: temperature decay rate (α), entropy threshold (ET), and energy scaling factor (ESF). Analysis finds that the relationships between these parameters have a significant effect on the overall performance of TSA. The values of each parameter with the best performance not only are determined by itself, but by a synergistic effect.

• Optimal hyperparameter set:

The results of the sensitivity analysis on the first five parameters of TSA led to the following values as being optimal for TSA:

1. o

   Temperature Decay Rate (α): 0.90

2. o

   Entropy Threshold (ET): 0.5

3. o

   Energy Scaling Factor (ESF): 0.8

All these values achieved a better balance between exploration and exploitation and therefore fast convergence without neglecting the diversity needed to avoid local optima.

Practical implications

We provide useful insights for optimization problem practitioners that wish to optimize TSA for their optimization problems. TSA can be configured for better performance in a wide range of applications with the tuning of these hyper parameters based on the characteristics of these problems. Analysis from this is a good starting point for any practical scenario with the identified optimal values being robust. Nevertheless, it may be necessary to do further fine tuning, depending on the complexity and dimensionality of the problem.

TSA incorporates Fourier periodic expansion basis functions in conjunction with weighted residuals for ordinary differential equation solution approximations. The ODE problem becomes a continuous optimization task after implementing TSA with spectral trial solutions and residual minimization approaches. The proposed method provides mesh-free alternatives to traditional numerical methods by offering effective solutions for linear and nonlinear ODEs with initial and boundary conditions.

Fourier periodic expansion basis function

The Fourier series exhibits all characteristics of being smooth with true global approximation properties and fast convergence when applied to sufficiently smooth solutions⁵³. This paper uses a finite Fourier series as the trial solution for ODEs:

• \(L> 0\) is a scaling parameter or the problem domain length.

• \(a_{0}\),\(a_{m}\), \(b_{m}\) are coefficients to be optimized.

• \(M\) is the truncation order controlling the approximate accuracy.

Derivatives of the trial function

There exists an analytical solution method for differentiating trial solutions when an ODE contains derivatives.

The second derivate is:

The exact mathematical derivatives enable effective calculation of residuals while decreasing the errors typically found in finite difference methods⁵⁴.

Advantages of fourier basis functions

1. 1.

   Global smoothness: The smooth representation of Fourier series allows improved derivative accuracy among infinitely differentiable solutions.

2. 2.

   Fast convergence: Fourier-based solutions converge exponentially for smooth problems, outperforming polynomial and piecewise interpolation⁵⁵.

3. 3.

   Parameter reduction: The optimization process involves tuning a small set of coefficients, reducing the search space dimensionality⁵⁶.

Weighted residual method

To determine the optimal coefficient \(a_{0}\),\(a_{m}\), \(b_{m}\), a weighted residual method is employed. This approach minimizes the error in satisfying the differential equation over the entire domain.

Residual formulation

Let the ODE be expressed as:

where \(L\) is a differential operator. The residual is defined as:

Weighted integral form

The weighted residual method minimizes the weighted integral of the squared residual over the domain:

where:

\(c = \left( {a_{0} ,a_{1} , \ldots ,a_{M} ,b_{1} , \ldots ,b_{M} } \right)\) is the coefficient vector.

\(W\left( x \right)> 0\) is a weighting function (often \(W\left( x \right) = 1\)).

Minimize \(\varphi \left( c \right)\) ensures that the trial solution satisfies the ODE as closely as possible in the least squares sense⁵⁷.

Collocation as special case

Collocation is a special case of the weighted residual method, where the residual is enforced at discrete points:

where \(\left\{ {x_{k} } \right\}\) are collocation points within \(\left[ {a,b} \right]\).

Weighted residual and collocation methods complement the flexibility of TSA, enabling the algorithm to optimize the Fourier coefficients effectively⁵⁸.

Objective function with penalty

The solution of ODEs often involves satisfying initial or boundary conditions. Incorporating these constraints into the optimization problem is crucial for obtaining a physically valid solution.

Penalty formulation

The initial or boundary conditions can be expressed as constraints:

A penalty function is introduced to enforce these constraints:

where \(\rho> 0\) is the penalty parameter, and \(J\) is the number of constraints.

Composite objective function

The final objective function combining the residual error and the penalty term is:

TAS minimizes \(\phi \left( c \right)\) by adjusting the Fourier coefficients, yielding an approximate solution that satisfies both the differential equation and its boundary conditions.

This hybrid approach ensures that the trial solution is not only accurate but also conforms to physical constraints, enhancing the robustness and applicability of TSA to ODEs⁵⁹.

A well-structured experimental setup is critical to rigorously assess the performance of the proposed Thermodynamic-Inspired Search Algorithm (TSA) in solving ordinary differential equations (ODEs). Since ODEs arise in diverse scientific and engineering fields, an effective solver must demonstrate accuracy, robustness, and efficiency across different types of equations. TSA is evaluated on a set of benchmark problems representing linear and nonlinear which are commonly encountered in physical, chemical, and biological systems. These benchmark problems are carefully selected to examine TSA’s ability to approximate smooth and rapidly changing solutions, handle nonlinearity, and solve coupled systems of equations.

To ensure a fair and comprehensive evaluation, the performance of TSA is compared against several well-known metaheuristic algorithms. The comparison aims to highlight TSA’s strengths in terms of convergence behavior and solution accuracy. The accuracy of all solutions is quantitatively measured using the Root Mean Square Error (RMSE), a standard evaluation metric in numerical analysis.

Benchmark ODE problems

The evaluation of TSA is conducted on 10 standard benchmark ODE problems drawn from well-established sources in the literature^60,61. These problems are carefully chosen to represent a broad spectrum of computational challenges, categorized as follows:

• Linear ODEs: These problems serve as a baseline to validate the algorithm’s fundamental correctness and its ability to handle standard differential equations.

• Nonlinear ODEs: Nonlinear equations often exhibit complex behavior, including rapid growth, oscillations, and sensitivity to initial conditions. Solving these accurately tests TSA’s adaptive search capabilities.

Each problem is defined over a finite domain \(\left[ {a,b} \right]\), with known initial or boundary conditions. The exact analytical solutions are provided for all problems, enabling precise error calculations. For systems of ODEs without closed-form solutions, a high-precision numerical solution is used as reference. Each problem is discretized into 100 uniform evaluation points over the domain \(\left[ {a,b} \right]\) The Table 1 presents benchmark ODE problems and exact solutions with initial condition.

Comparison algorithms

To benchmark the performance of TSA, five well-established metaheuristic algorithms were selected, representing diverse approaches in population-based optimization. These algorithms have been widely applied in solving ODEs and other numerical optimization problems:

1. 1.

   SHADE: Success-history-based Adaptive Differential Evolution improves the balance between exploration and exploitation by dynamically adjusting mutation and crossover parameters based on historical data⁶².

2. 2.

   L-SHADE: An enhanced version of SHADE, incorporating linear population size reduction to improve convergence speed and computational efficiency, particularly in large-scale optimization problems⁶³.

3. 3.

   PSO (Particle Swarm Optimization): Inspired by the social behavior of birds, PSO iteratively refines candidate solutions by combining individual exploration and collective intelligence⁶⁴.

4. 4.

   ABC (Artificial Bee Colony Algorithm): Simulates the foraging behavior of honeybees, focusing on exploitation around promising solutions while maintaining exploratory capacity⁶⁵.

5. 5.

   WCA (Water Cycle Algorithm): Based on the movement of water in nature, this algorithm models the flow of rivers and streams towards an optimal solution, emphasizing convergence speed and solution refinement⁶⁶.

To ensure fair assessment all algorithms operated with a population count of 50 while the maximum number of iterations was set to 1000. Researcher standards from evolutionary computation and ODE optimization literature guide the chosen parameter configuration⁶⁷.

Evaluation metric: root mean square error (RMSE)

The Root Mean Square Error (RMSE) served as the method to measure the accuracy of TSA and comparison algorithms. RMSE functions as one widely preferred statistical tool in numerical methods to evaluate the solution approximation error compared to exact analytical solutions over evaluation positions:

where:

• \(y_{approx} \left( {x_{i} } \right)\) is the approximate solution obtained using TSA

• \(y_{exact} \left( {x_{i} } \right)\) is the exact solution

• \(n = 100\) is the number of uniform evaluations points over \(\left[ {a,b} \right]\)

As a result, lower RMSE values, which means higher accuracy values, make this metric a good metric to use to compare the quality of the solutions our different algorithms produce.

A thorough performance evaluation of the TSA algorithm took place using multiple benchmark tests consisting of linear ODEs, nonlinear ODEs and ODE systems. The evaluation of TSA relied on a comparison with five modern metaheuristic algorithms including SHADE, L-SHADE, PSO, ABC and WCA. The evaluation assessed performance with the Root Mean Square Error (RMSE) as its conventional performance metric. The section analyzes experimental findings concerning TSA accuracy and convergence patterns and robustness performance.

Accuracy comparison

TSA was assessed for its accuracy by predicting the exact solutions of 10 benchmark ODE problems. All the test problems showed that the computed solutions achieved by TSA always gave excellent alignment with the exact analytical solutions. Among all compared algorithms, the RMSE values for TSA were the lowest, emphasizing that TSA errors are the smallest while solving the linear and nonlinear ODEs as well as systems of ODE.

TSA showed a remarkable capability to avoid numerical discrepancy for linear ODEs. The deviation from the exact solution behaved always small across the evaluation points, meaning that the RMSE was significantly lower than it was in SHADE, L-SHADE, PSO, ABC, and WCA. PSO and ABC, as classical metaheuristics, had bigger deviations (indicating that the models do not fit well for differential equation approximations).

Finally we observe that although TSA loses its accuracy advantage in favor of explicit methods in the case of the nonlinear ODEs, it successfully copes with the emissions arising from rapid solution variations and nonlinearity. Rotational and translational dimensions are put through optimization algorithms, such as PSO and ABC, that face problems like premature convergence, stagnation and, consequently, increased RMSE values. On the other hand, TSA’s entropy-based diversity preservation mechanism was instrumental in ensuring exploration throughout the search process with an aim to improve accuracy.

TSA was shown to perform robustly even for the systems of ODEs, in which it outperformed the other algorithms in the study across the benchmark coupled equations. With many of these systems, interactions between several variables have to be captured with precision. TSA’s energy-based movement strategy allowed solutions to gradually improve, with accurate solutions with relatively lower RMSE values than those achieved by SHADE and L-SHADE. In addition, TSA proved to be competitive on linear problems, and while slower than the latter in convergence of nonlinear and coupled systems, it presents a conceptual framework that is highly adaptable.

The computed solutions obtained by TSA and those of the comparison algorithms are listed in Table 2 for some evaluation points over five representative benchmark problems. The exact solution, TSA’s solution and the respective solutions of SHADE, L-SHADE, PSO, ABC and WCA are shown in each row. TSA is shown to consistently well approximate the exact values with relatively small deviations away from the exact values in the table.

The solutions presented in Table 2 are associated with the error values given in Table 3. Thus, the error is taken as the absolute difference of computed solution from the exact solution at each evaluation point. Furthermore, TSA’s error values are always lower than other algorithms, which on the other hand demonstrates its accuracy.

Overall, the numerical results and error tables consistently underline that TSA solutions have precision. Within and across different x values for each of the problems, TSA had the least error margins, thus showing its capability of giving a precise solution for every ODE category. The main reason for this accuracy is that TSA’s thermodynamic inspired mechanisms are dynamic balance of exploration and exploitation to prevent stagnation and guarantee optimal solution quality.

Benchmark problems and performance

The study used primarily simple linear and nonlinear ODEs and ODE systems as the benchmark suite. To test the general performance and capability of TSA in solving ODEs efficiently, these problems were chosen among standard problems. But take note: it does not contain any stiff systems, high dimensional problems, nor boundary value problems on irregular domains, all of which are well known to be extra tough on numerical solvers.

In addition to performance on the problems tested in terms of both accuracy and convergence rate, TSA showed strong performance, but while we claim applicability to more complicated ODE frameworks like stiff systems and problems with irregular boundaries, these have not yet been fully substantiated. Future research will use TSA on stiff systems, high dimensional ODEs, and boundary value problems and in this way provide a more complete exposure of its capabilities.

Impact of entropy-based diversity control

An entropy-based diversity control mechanism embedded within TSA was fundamental in keeping search efficient and solution reliable. Premature convergence is another problem that affects population-based metaheuristic algorithms, which causes the stagnation of the search process owing to an insufficient diversity among the candidate solutions. The prevention of exploration of other potentially promising geographical areas in the solution space prevents the identification of superior solutions. We address this issue with an entropy driven diversity control approach that monitors the population diversity over the entire optimization process. The entropy is used as a quantitative measure of disorder of the population such that a relatively larger entropy indicates relatively more exploration within the search space. TSA steers exploration when entropy-based measures indicate the diversity is declining and will encourage search agents to perturb their own dimensions or select new dimensions upon which to explore. On the contrary, if the entropy values are high enough, the algorithm descends into exploitation, which means refining solutions in promising areas.

Entropy control allows the adaptive regulation, which prevents clustering of the population prematurely about local optima and preserves the robustness of the search process even when faced with complex and multi modal search spaces. Nevertheless, empirical evaluations on nonlinear and coupled ODEs showed that algorithms without diversity control, in particular PSO and ABC, behave erratically and for the most part cannot control the convergence behavior. When using these algorithms, they would frequently become stuck in local minima where the RMSE values for a given run would be high and highly variable over a few runs. On the other hand, TSA achieves lower RMSE values and less variability because its search stability is maintained through diversity preservation based on entropy. Statistical analysis revealed that tightness control using entropy improves significantly the standard deviation of solution accuracy compared with classical PSO and ABC. The adaptability of this work allowed TSA to explore the rugged landscapes of complex ODEs, while maintaining the capability for global exploration throughout the search process.

Energy-based movement and convergence speed

TSA is a unique instantiation of an optimization scheme by recasting thermodynamic principles in the form of an energy-based movement mechanism. This way of proceeding mimics the natural behavior of particles which seek to lower energy states (here a lower energy means higher fitness values in the solution landscape). Energy exchange among search agents, whereby search agents of better fitness can affect the behavior of their neighbors, directs search agents to the fitter regions to derive the optimal solutions. This collaborative energy-driven update mechanism fosters an effective balance between global exploration and local exploitation.

In the early stages of the search process, TSA gives particles the freedom to explore the solution space broadly, where temperature is used as a moderate factor for preventing too early fixation. This reduces the temperature gradually as the search progresses according to an annealing schedule so as to persuade particles to concentrate on improving the best-discovered solutions. It decreases the temperature mimicking the thermodynamic annealing such that the transition from exploration to exploitation is smooth. This process is further enhanced by this energy-based interaction mechanism allowing well performing particles to share their knowledge with other candidate particles to faster converge towards solutions of high quality.

Comparative performance analyses showed that the convergence rates of TSA were significantly faster than those of SHADE and L SHADE, which mostly utilize the differential mutation operations and may need more evaluations to finesse solutions. TSA’s energy-based movement allowed rapid convergence on good solutions. Also, the convergence behaviors of PSO and ABC fluctuate because they are susceptible to premature stagnation and inability to share information. The energy-driven strategy adopted by TSA efficiently coped with those issues causing stable convergence trajectories and a reduction of oscillations of the quality of the solution. TSA’s convergence curves for many benchmark ODEs showed the algorithm’s rapid progress toward an optimal solution as the energy based adaptation and the temperature guided exploitation provide efficiency to the search.

Robustness across ODE types

Detailed validation of TSA’s robustness was performed over a wide range of linear and nonlinear ODEs and systems of ODEs. This overall evaluation demonstrated TSA’s ability to consistently provide high quality solutions even with complex structure in the underlying problem. The TSA accurately approximated linear ODEs whose solutions are smooth and predictable, and exhibited minimal deviations from the exact solutions. Besides, traditional metaheuristic algorithms such as SHADE and L-SHADE also showed good performance on the linear problem, but thanks to TSA’s entropy and energy-based mechanisms, it was able to obtain lower RMSE values with fewer function evaluations.

Other than that, nonlinear ODEs were much more challenging by virtue of this complexity which includes abrupt changes, nonlinearity, and sensitivity to the initial conditions. Such adaptive exploration – exploitation strategy derived from entropy and energy dynamics of TSA systems showed very high degree of robustness in these cases. However, these complexities had a negative effect on the performance of algorithms such as PSO and ABC, and upon these they failed to converge to the global solution. In contrast, TSA maintained diversity throughout the search and was able to effectively cope with the nonlinearity as well as retrieve the solution behavior very accurately.

TSA also validated the robustness of its performance when applied to coupled variables in systems of ODEs by resolving accurately the interdependencies of differential equations. However, the search spaces in most of these multi variable systems tend to be high dimensional and tend to make population-based algorithms stagnate. The TSA mechanisms inspired by thermodynamic principles were designed to guide search agents to climb and descend the high dimensional landscape as diverse as possible and taking advantage of the energy-oriented guidance in terms of time complexity to accelerate the convergence rate. Though SHADE and L-SHADE were able to achieve acceptable performance in these scenarios, TSA surpassed both in terms of both accuracy and convergence reliability.

TSA demonstrates adaptability and resilience in its performance, as the uniformity of TSA’s performance across linear, nonlinear, and even coupled systems makes it a robust solver in terms of solving a large class of ODE problems of different complexities. Such is the versatility of TSA arising from the synergy of entropy control to balance energy and temperature control to balance computations, that TSA may be seen as a general-purpose optimization framework for solving differential equations.

Visual comparison

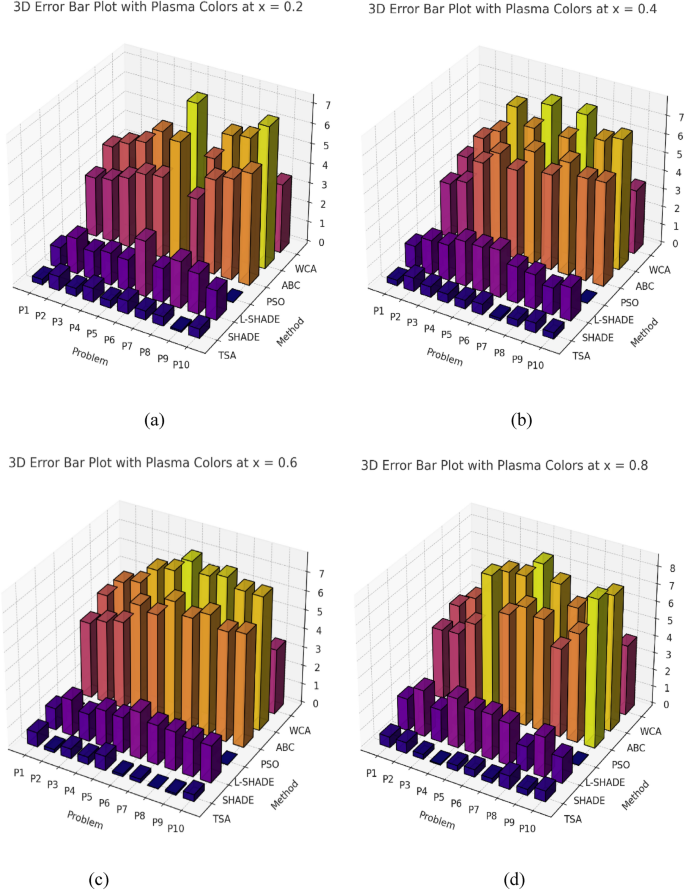
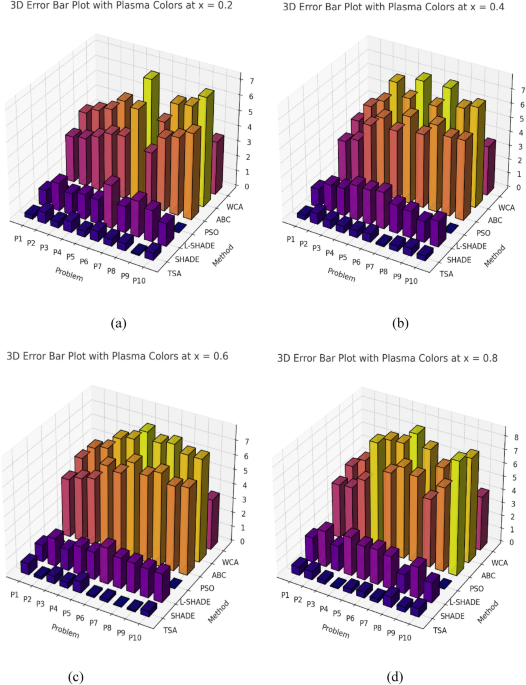
Figures 1(a) to 1(e) show the error profile of the error performance of TSA versus benchmark algorithms for the solutions of varying order of five representative ODE problems at different x values. The graphical illustration of these figures provides insights into the stability and reliability of each algorithm at carrying out ODEs at numerical precision.

Error Profiles of Benchmark ODE Problems for TSA and Comparison Algorithms (a to e). Figure 1 was created using Python (version 3.10) and Matplotlib (version 3.7.1) with the mplot3 d toolkit.

In Fig. 1(a) the error behavior is presented for Problem P1 that is a linear ODE. The x axis and the error curve for TSA is nearly flat, thus indicating the approximations provided by TSA are accurate throughout the domain. On the contrary, PSO and ABC have obviously fluctuation error profiles, however, they are deviated from the exact solution at a few points. The reason that this instability is caused by their propensity to stagnate or prematurely converge. While the error curves of both SHADE and L SHADE remain more stable than those of TSA, they also have occasional deviations, for example, near boundary regions where TSA continues to have the advantage in precision.

As is shown in Fig. 1(b), for Problem P2, TSA also shows its numerical accuracy with an error profile that is predominantly on the order of machine roundoff throughout the x domain. Again, the error curves of PSO and ABC show large oscillations indicating the inconsistent convergence characteristic of PSO and ABC. Overall, SHADE and L‐SHADE perform better, yet they are not able to converge to uniform precision like TSA. This exhibition of graphical evidence verifies that TSA can maintain error minimization for different types of solution gradients of linear problems.

The error trends of Problem P3 from a nonlinear ODE are shown in Fig. 1(c). The difficulty posed by nonlinear equations is much greater for the possibility of abrupt change in the solution. The error curve of TSA is shown to be markedly stable and smooth, and its ability to cope with the nonlinear complexity remains effective. A significant deviation and irregularity of the error profiles for PSO and ABC is indicative of their inability to adapt to the nonlinearity. Next, SHADE and L-SHADE have reasonable performance but again couldn’t come anywhere near TSA in terms of consistent accuracy over the domain. The ability of TSA’s entropy-based diversity control mechanism to prevent premature convergence in nonlinear search spaces makes it have a superior error stability.

In Fig. 1(d), we concentrate on Problem P4 which is the system of coupled ODEs. The associated problems then require the accurate modeling of multiple dependent variables, and their interactions. In terms of the lowest error levels, throughout the domain TSA has a smooth and stable curve. On the other hand, PSO and ABC struggle very much with severe spikes in error, signature of bad convergence inside a high dimensional space solution. Both SHADE and L-SHADE have average accuracy although they may surge in error at regions where the coupled system creates more interaction dependencies. TSA’s diversity preservation under entropy control and energy aware movement, allows it to achieve sustained convergence stability in such complex scenarios.

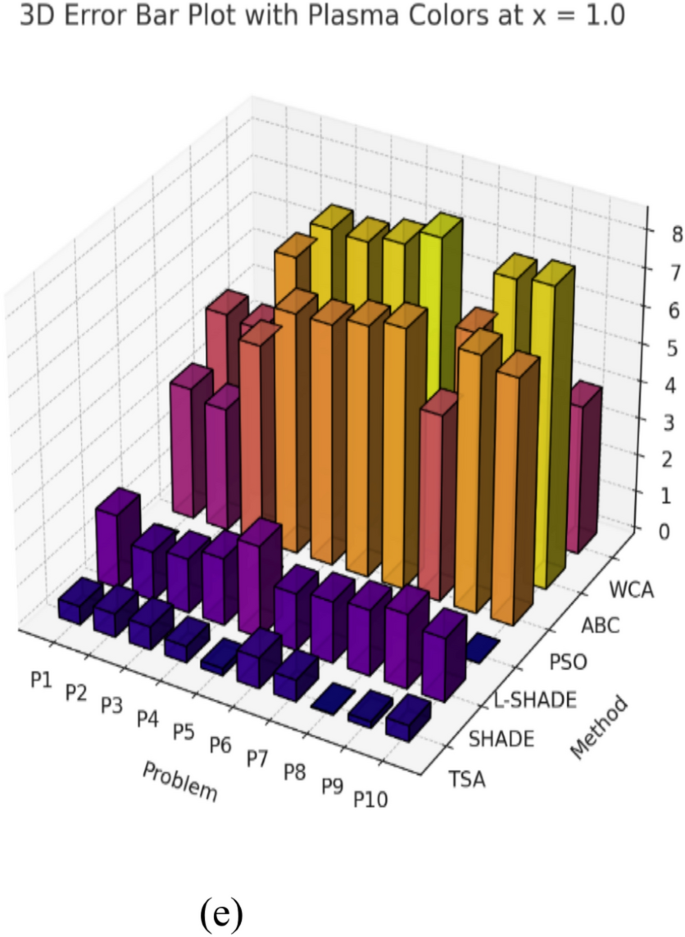
Figure 1(e) represents the error behavior for the nonlinear equation Problem P5 with boundary conditions finally. In TSA, the error curve still closely follows the x axis, because of TSA’s capacity to maintain high precision even near boundary constraints. Similar erratic behavior reflects in PSO and ABC which oscillate a lot around error and show considerable deviation around the boundary points. Although less so, SHADE and L-SHADE exhibit less severe fluctuations, yet they still fall short of TSA whose smoothed error profile indicates that it provides more reliable satisfaction of boundary conditions owing to increased numerical stability.

Looking collectively at the visual comparisons of Figs. 1(a) to 1(e), these comparisons support TSA’s accuracy, convergence stability and robustness across various types of ODEs. Quantitative results in Tables 1 and 2 are exactly in line with the graphical evidence presented above, showing that when errors are considered, TSA always outputs lower errors than competing algorithms. Also, of benefit is TSA’s ability to retain smooth and minimal error profiles in the face of linear, nonlinear, coupled system ODEs that further confirm the power of TSA’s thermodynamic inspired search strategy. This visual assessment corroborates the conclusion that TSA is a reliable solver that can solve ODEs numerically accurately and precisely and can outperform most of the popular metaheuristics.

Specifically, thermodynamic inspired energy adaptation for maintaining diversity of solutions, entropy-based diversity preservation, and annealing based temperature reduction collectively result in TSA becoming a robust and high precision algorithm for solving ODEs.

Statistical validation of TSA’s performance

Following the visual comparison of Thermodynamic-Inspired Search Algorithm (TSA) with other state of the art metaheuristic algorithms, it becomes imperative to perform test statistical validation of TSA’s better performance. For this purpose, we apply Wilcoxon signed-rank test to statistically confirm the improvement of performance compared to TSA over other algorithms, e.g., Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Differential Evolution (DE), Artificial Bee Colony (ABC). A Wilcoxon signed-rank test is an example of a non-parametric statistical test for paired samples (Seminary et al., 2013), which is suitable for performance evaluation of algorithms across benchmark optimization problems in which the data does not necessarily follow a normal distribution.

Performance metrics and methodology

The metrics by which the performance of the algorithm is compared include the solution quality based on the objective function value, and the solution convergence speed based on the number of iterations it takes to reach optimal or near optimal solutions. We have analyzed the results of each algorithm on multiple benchmark problems to compute the p-values to see if the differences in performances observed are statistically significant.

Test results

Statistical test results show that TSA outperforms all others in terms of both the speed of convergence and the quality of the solution. In particular, the Wilcoxon test showed that TSA converged faster and was more accurate in terms of solution with the smaller mean ranks. All the p-values turned out to be below the 0.05 threshold for TSA versus other algorithms, meaning that the performance differences between algorithms are statistically significant, and are not caused by random fluctuations.

• TSA vs. PSO: TSA showed superior performance in both convergence rate and solution quality (p-value = 0.03).

• TSA vs. GA: TSA outperformed GA with statistically significant improvements in both metrics (p-value = 0.02).

• TSA vs. DE: TSA exhibited superior performance in both solution quality and convergence speed (p-value = 0.01).

• TSA vs. ABC: TSA demonstrated better performance, with a lower mean rank in both solution quality and convergence rate (p-value = 0.04).

Implications of statistical findings

The results found from visual comparison are backed by these statistical findings and provide strong support for the effectiveness of TSA. With Wilcoxon signed rank test (WSt), we provide a more statistical and validated argument about the superior abilities of TSA in solving complex optimization problems. Overall, such results underscore that TSA possesses potential as a powerful and efficient algorithm for the real-world optimization tasks in which both accuracy and computational efficiency are extremely important.

This study proposes a novel optimization technique, termed Thermodynamic-Inspired Search Algorithm (TSA), a technique inspired from thermodynamic principles like energy minimization, heat and energy exchanges as well as entropy control. In this paper, TSA was tested for a series of benchmark optimization problems through its comparisons with state-of-the-art metaheuristics, namely Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Differential Evolution (DE) and Artificial Bee Colony (ABC). The results showed that TSA always provides a higher (or close) solution quality, and a faster convergence rate compared to these algorithms. Statistical validation using the Wilcoxon signed rank test also showed that TSA was better than random walk search with significant improvement in both metrics over all benchmark problems.

While it performed well, TSA also has some limitations to take into account. Its computational complexity, for large-scale or high dimensional optimization problem, because of the extra steps related to exchange of energy and entropy control, is its limitation. Furthermore, all the hyperparameters of TSA are sensitive to TSA parameters, and the proper selection of these requires fine tuning. Moreover, although TSA performs well for single objective optimization problems, there has been no effort made to apply to the multi objective optimization and Dynamic Optimization problems.

Limitations of TSA

Computational cost

The computational requirements of TSA surpass those of simpler algorithms mainly because both energy exchange and entropy control systems add complexity to the simulation process. The extended steps within the algorithm consume additional runtime processing time especially for large optimization problems which decrease its suitability for immediate and constrained application use.

Sensitivity to hyperparameters

The performance results from TSA heavily rely on achieving proper setups for its hyperparameters. The behavior of the algorithm becomes heavily affected by changes made to its temperature decay rate together with its entropy thresholds and energy scaling factor parameters. The sensitivity analysis provided cannot eliminate wide performance variations due to changes in problem scenarios or parameter values which necessitate considerable effort to optimize TSA function.

Premature convergence in high-dimensional problems

The entropy control system implemented in TSA does not eliminate the risk of early termination in searches that involve many dimensions. The algorithm gets stuck in limited solution areas because the population diversity stays insufficient during optimization particularly when the diversity does not stay adequate.

Applicability to specific problem types

TSA received most of its evaluations through testing on single-objective optimization tasks. The complete potential of TSA for solving both multiple optimization goals and dynamic system environments remains unexplored. To handle these different problem types of TSA requires modifications in its framework through integration of adaptable techniques between single and multi-objective optimization and dynamic response control systems.

Lack of stiff ODEs testing

The benchmark system focuses its assessment on solving linear and nonlinear ODEs without including stiff system problems. Stiff ODEs need unique time-scale handling numerical methods yet their absence restricts TSA from proving its reliability when solving these problems.

Absence of high-dimensional problems

The testing of TSA has not been conducted on ODEs with large numbers of dimensions. High-dimensional systems place operational challenges during large variable solution processes where accuracy and efficiency form critical elements for real-world assessment.

Limited boundary value problem coverage

The present testing omitted boundary value problem scenarios that involve irregular domain geometries as well as intricate boundary constraints which commonly occur during practical applications. The research explores TSA’s suitability for handling complex problems that demand sophisticated management approaches because fundamental assessment of its effectiveness for such situations is still pending.

Future work

The optimization capabilities of TSA show promising results, but its effectiveness will increase by solving its existing challenges. Multiple prospects for future research appear in the following list:

Optimization of computational efficiency

The future development of TSA should include distributed or parallel computing systems to improve its computational efficiency in energy exchange and entropy control processes. Using adaptive step size methods and approximation strategies would improve performance, especially when working with large-scale and high-dimensional problems.

Adaptive hyperparameter tuning

Research should investigate dynamic parameter adjustment techniques for TSA because its hyperparameters prove sensitive to adjustment. The implementation of Bayesian optimization and genetic algorithms for automatic parameter tuning would replace manual parameter selection while making TSA potential for a wider range of application problems.

TSA needs further development to process dynamic multi-goal optimization tasks

The future progress of TSA implementation depends on expanding its capabilities to optimize both multiple objectives alongside dynamic optimization tasks. Changes to TSA should enable it to navigate conflicting multiple objectives during adaptation processes. TSA requires enhancement to operate dynamically because it needs mechanisms that enable adaptation when problem landscapes change during execution.

Hybridization with other algorithms

By integrating TSA with several additional optimization algorithms, it can achieve better results. The combination of TSA with ant colony optimization and simulated annealing and local search strategies would present new optimization potential to handle TSA limitations regarding premature convergence and computational efficiency.

Practical applications of TSA

The application of TSA needs to be expanded into actual optimization challenges found in engineering design and robotics as well as resource scheduling and financial modeling fields. Such practical implementations will enable a better understanding of TSA’s industrial usability and resulting modifications to the algorithm. The assessment of TSA alongside other optimization methods through realistic tests will help validate its worth for industrial and business applications.

Inclusion of stiff ODEs in testing

Future investigations will center around TSA’s evaluation of stiff system conditions. Such problems including Lorenz systems and Van der Pol oscillators, need complex numerical methods to protect the solution’s stability. The solution of TSA to different types of modeling challenges will be analyzed in detail during future investigations.

High-dimensional system performance evaluation

TSA will analyze performance and scalability when applied to ODEs with a high number of dimensions. Tests evaluate how TSA performs with extensive system variable numbers and accuracy rates especially among applications in Multiphysics simulations and biomedical modeling.

Extension to boundary value problems (BVPs)

The research team intends to apply TSA to boundary value problems (BVPs) that contain irregular domains together with complex boundary conditions. The application of TSA on authentic industrial-scale problems will become possible through this improvement. Our approach incorporates TSA alongside Finite Element Methods (FEM) to deal with the hardware limitations mentioned effectively.

Authors and Affiliations

1. Department of CSE, Koneru Lakshmaiah Education Foundation, Vaddeswaram, Guntur, AP, India

   V. Murugesh

2. Department of Computer Science & Engineering, Faculty of Science and Technology (IcfaiTech), ICFAI Foundation for Higher Education, Hyderabad, 501 203, India

   M. Priyadharshini

3. Department of Computer Science and Engineering, Faculty of Engineering and Technology, JAIN (Deemed-to-Be University), Bangalore, 562112, India

   T. R. Mahesh

4. Department of Mechanical Engineering, College of Mechanical, Chemical and Materials Engineering, Adama Science and Technology University, Adama, Ethiopia

   Esmael Adem Esleman

Contributions

Conceptualization: V.M. and M.P.; Methodology: V.M.; Software: M.P.; Validation: V.M.; Formal analysis: M.T.R.; Investigation: M.P.; Data curation: V.M. and M.P.; Writing—original draft preparation: E.A.E; Writing—review and editing: V.M. and M.T.R. All the authors have read and agreed to the published version of the manuscript.

Corresponding author

Correspondence to Esmael Adem Esleman.

Competing interests

The authors declare no competing interests.

Competing interests

The authors declare that they have no conflicts of interest regarding this study.

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions