Machine-learning design of ductile FeNiCoAlTa alloys with high strength

Metallic alloys with extraordinary strengths are highly sought after for challenging structural applications. The state-of-the-art bulk alloys have now reached yield strength (σ_y) of approximately 2 GPa while retaining adequate tensile ductility (ε exceeding 8%)^1,2,3,4. For example, such a strength–ductility combination has been accomplished in a few ultra-strong steels^1,2,3, including deformed and partitioned (D&P) medium-Mn steels² with C concentrations of approximately 0.18–0.47 wt%. However, these steels have inadequate work hardening capability and, consequently, often suffer from extensive Lüders bands or Portevin–Le Châtelier bands. As such, much of the reported uniform elongation (ε_u) in standard uniaxial tensile test consists of serrated plastic flow caused by C solute-induced deformation bands, rather than truly uniform elongation. When Lüders bands are absent, such as in some 2-GPa maraging steels, ε_u is limited to approximately 3.8% (ref. ¹).

One potential pathway to surpass these steels in reaching high σ_y and large ε_u simultaneously is to resort to recently emerging high- and medium-entropy alloys (HMEAs), in which multiple principal elements are adopted to form compositionally complex alloys. However, this approach has not yet fulfilled its promise. Although many high-entropy alloys (HEAs) have been developed, often on the basis of a face-centred cubic (FCC) phase (dominant) with high ductility and toughness, their yield strength is generally relatively low^5,6. In addition to solute atoms (or local chemical order (LCO))⁴, grain boundaries⁷ and twin boundaries⁸, nanoprecipitates can mitigate, to some extent, the strength–ductility trade-off in numerous alloys, such as Al alloys⁹, steels^1,10,11 and Ni-based superalloys^12,13, in which the nanoprecipitates act as dislocation obstacles and sources^14,15,16 and encourage dislocation entanglement to increase strain hardening. Unfortunately, as summarized later, these nanoprecipitation-hardened HEAs manifest a σ_y below 1.2 GPa (refs. ^17,18). This is a result of the limited fraction (less than 55 vol%) of nano-scaled multicomponent intermetallic precipitates (MCIPs). A heterogeneously structured CoCrNi-based alloy achieved σ_y of approximately 2 GPa and ε_u of approximately 13%. However, this alloy requires complicated processing, including cryo-rolling at 77 K (ref. ¹⁹). In addition, in ultra-high-strength HEAs, the reported ε_u can be largely mediated by Lüders bands propagating from one end of the gauge length to the other. An example is the nominal ε_u of approximately 16% claimed in an anisotropic (Ni_1.5FeCoCr_0.5)_87.5Al_7.5Ti_5.0 HEA with a lamellar structure, achieving σ_y of approximately 2 GPa and ultimate tensile strength σ_UTS of approximately 2.1 GPa (ref. ²⁰). Another example is the medium-entropy alloy VCoNi, which reached 2 GPa, but its rising stress–strain curve was preceded by Lüders strain⁴. To bolster strength, one alternative was to involve incoherent B2 precipitates in combination with L1₂, an example being the FeNiCoAlTaB system. However, its B2 content was far from enough to produce satisfactory strength, obtaining merely σ_y of approximately 1 GPa and σ_UTS of approximately 1.4 GPa, although ε_u reached approximately 20% (ref. ²¹). In summary, the available HMEAs fall short in surpassing the state-of-the-art steels, and approximately 2-GPa HMEAs with large and truly uniform tensile ductility have yet to be discovered.

A question that naturally arises is how far one can reach towards the upper-right corner of the strength–ductility plot (shown later). The search for suitable HMEAs faces an enormous composition space. Active learning is widely recognized for its efficiency in navigating vast design spaces, but it involves many iterations and complex models to effectively shortlist candidates for experiments²². Our approach incorporates domain-specific knowledge, which narrows down the scope and enhances the performance of the machine learning model (Supplementary Note 1). Eventually, a multi-principal-element alloy with a composition of Fe₃₅Ni₂₉Co₂₁Al₁₂Ta₃ was identified. Subsequent post-casting processing (various rolling and heat treatment parameters) achieved our objective. The yield strength–uniform ductility combinations range from 1.5 GPa (31%) to 1.95 GPa (15%), covering a territory previously inaccessible for all bulk alloys. A prominent example, discussed at length below, delivers a σ_y of 1.75 GPa, σ_UTS of 2.4 GPa (the corresponding true stress is as high as 3 GPa), a high work hardening rate (WHR, Θ) sustained at higher than 2 GPa and ε_u of 25%.

The following domain knowledge aided in the selection of composition and processing: (1) Atomic size misfit maximization for pronounced solid solution strengthening—given both a large atomic size mismatch and a large negative mixing enthalpy (Supplementary Table 1) after adding AlTa into the FCC matrix, a high strength is projected for FeNiCoAlTa HEAs²³. (2) A very high fraction of strong L1₂ coherent nanoprecipitates—normally, high-solubility and fast-diffusing solutes (such as Al) favour nanoprecipitates with a large volume fraction^9,24. Here we deliberately assembled a high content of Al and L1₂-promoting Ta solutes into the FeNiCo base alloy to help generate high-volume-fraction coherent L1₂ nano-MCIPs. The anti-phase boundary energy γ_APB of Ta-containing L1₂ MCIPs, which is higher than that of Ti-containing L1₂ previously used for strengthening (σ_y of less than or equal to 1.2 GPa (refs. ^17,18)), enhances precipitation strengthening. (3) An appreciable fraction of ductile B2 incoherent microprecipitates at high Al concentrations that contributes to strengthening on top of the L1₂ nanoprecipitates—compared with the traditional hard/brittle intermetallic inclusions, the chemically complex MCIPs with several components show lower chemical ordering energy (Extended Data Fig. 1) and γ_APB, which is expected to facilitate dislocation slip and enhance plasticity^1,2,3,18. These B2 micro-MCIPs could accommodate ample dislocation activities with no worries of (local) stress concentrations and accumulate dislocations inside to promote WHR for enhanced uniform elongation.

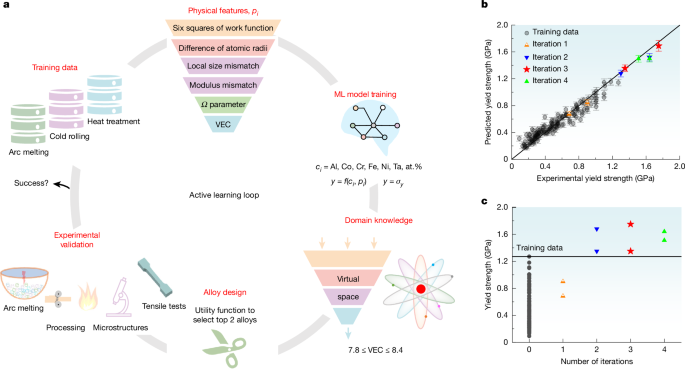
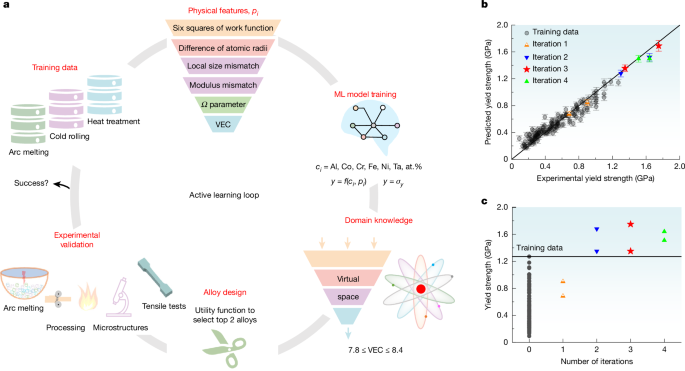
Figure 1a shows the iterative loop of active learning aimed at optimizing alloy compositions for high strength, starting from a dataset comprising 140 FCC HEAs within the AlCoCrFeNiTa alloy system, with the measured σ_y and elongation to fracture, ε_f (Supplementary Fig. 2). All alloys reported in the literature or produced in our laboratory were prepared through arc melting, followed by homogenization, cold rolling and heat treatment. From a pool of 20 physical features (Supplementary Table 2), as shown in Fig. 1a, six were selected (Supplementary Fig. 3a) as the domain knowledge input for the machine learning surrogate model aimed at reducing model complexity, given that the model performance does not significantly improve with extra features. The detailed machine learning model about target alloy design is presented in Supplementary Note 1. Figure 1b compares all four iterations with the training data; six of the eight newly synthesized alloys showed higher σ_y. Most data points were very close to or even located right on the diagonal line (Fig. 1b), further verifying the high reliability and robustness of our machine learning model. Figure 1c shows the relationship between the improvement in σ_y with increasing iteration, and the desired alloy was achieved after the third iteration. The Fe₃₅Ni₂₉Co₂₁Al₁₂Ta₃ alloy, hereafter referred to as the HEA05 alloy, had the highest σ_y among all compositions (Supplementary Table 4).

a, The domain knowledge-based active learning loop consists of six steps: (1) training data collection; (2) physical descriptor inclusion; (3) machine learning (ML) model training; (4) virtual space narrowed through domain knowledge; (5) alloy design by utility function; and (6) experimental validation and feedback. b, Plot of predicted σ_y versus experimental σ_y of the eight newly synthesized alloys from the four iterations, as well as the training data, showing the high reliability and robustness of the present ML model. c, Experimental σ_y versus the number of iterations, showing the optimized σ_y of the HEA05 alloy at the third iteration.

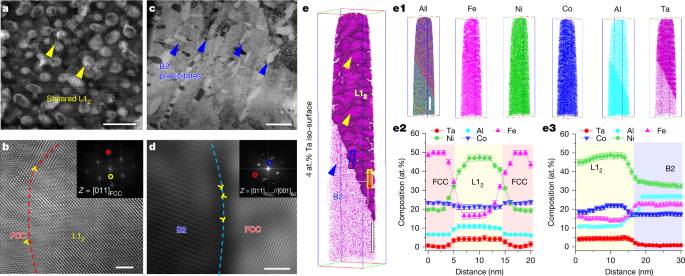
We now focus on the best-performing HEA05, with reference to its base alloy, A0 (Fe₃₅Ni₂₉Co₂₁)₁₀₀Al₀Ta₀ (normalized to Fe₄₁Ni₃₄Co₂₅), the Al-alloying-only (Fe₃₅Ni₂₉Co₂₁)₈₈Al₁₂ and the Ta-alloying-only (Fe₃₅Ni₂₉Co₂₁)₉₇Ta₃. HEA05 processed at 750 °C for 1 h of ageing was used as a representative. Although machine learning directed us to this composition, the microstructures inside were essential for the properties. By highly alloying with both Al and Ta, we successfully introduced densely dispersed L1₂ coherent nano-MCIPs and low modulus-yet-hard deformable B2 incoherent micro-MCIPs (Extended Data Fig. 2, Supplementary Fig. 6 and Supplementary Note 2) into the FCC matrix having randomly oriented equiaxed grains with the average size (d) of approximately 7.6 µm (Fig. 2 and Extended Data Fig. 3). As shown in Fig. 2a, near-spherical L1₂ nano-MCIPs with d of approximately 15 ± 3 nm were uniformly distributed inside the grain interiors with a volume fraction as high as 66.6 ± 2.3%, as measured using small-angle X-ray scattering (SAXS; Extended Data Fig. 4). The B2 micro-MCIPs formed during the casting process have a typical dimension of 350 ± 70 nm, with a length-to-width aspect ratio averaging approximately 3.1 (Extended Data Fig. 3) and a volume fraction of 15 ± 2%, residing between FCC grains. The interfacial mismatch strain can be determined from the wide-angle X-ray scattering (WAXS) patterns (Extended Data Fig. 5) to be approximately 0.24 ± 0.03% and 22.8 ± 0.01% for the L1₂/FCC and B2/FCC interfaces, respectively. Apparently, Ta, Al and Ni elements primarily partitioned to the L1₂ nano-MCIPs and Al and Ni elements to the B2 micro-MCIPs, whereas Fe and Co were largely depleted from both types of precipitates (Fig. 2e(1–3), Extended Data Fig. 6, Supplementary Fig. 7 and Supplementary Note 3). The results are summarized in Supplementary Table 5.

The alloy was aged at 750 °C for 1 h. a, Scanning transmission electron microscopy (STEM) image of L1₂ precipitates in the FCC matrix after tensile deformation to 5% strain, with the corresponding selected area electron diffraction (SAED; inset). Two examples of dislocation-sheared L1₂ precipitates are marked using yellow arrows. b, High-resolution transmission electron microscopy image showing the FCC/L1₂ interfaces (with dislocations after 5% strain) and the corresponding fast Fourier transform pattern (inset). c, STEM image of B2 precipitates located close to one another in the FCC matrix. Blue arrows indicate several examples of B2 precipitates. d, High-resolution transmission electron microscopy image showing the FCC/B2 interfaces having Kurdjumov–Sachs relationship: (111)_FCC//(110)_B2 and [110]_FCC//[111]_B2 at 5% strain, with the corresponding SAED (inset). e, Atom probe tomography (APT) results of HEA05 alloys with 4 at.% Ta iso-concentration surface: respective elemental distribution of FCC, L1₂ and B2 phases (e1); composition profile across FCC–L1₂ (e2); and composition profile across L1₂ and B2 phases (e3). Scale bars, 50 nm (a,e,e(1)), 2 nm (b,d), 500 nm (c).

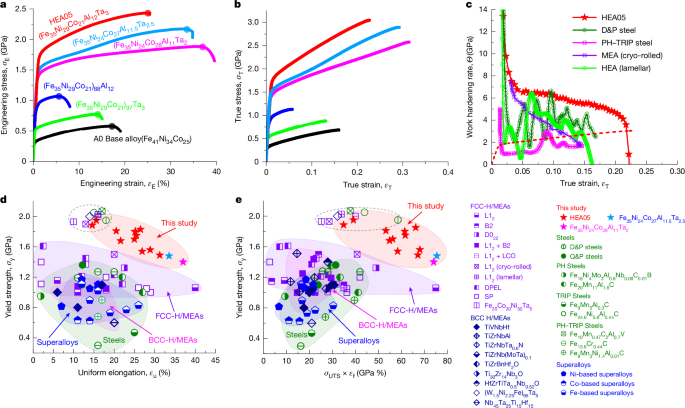
The highly heterogeneous microstructure consisting of dual precipitates in the FCC concentrated solid solution (‘matrix’) endows the HEA05 Fe₃₅Ni₂₉Co₂₁Al₁₂Ta₃ alloys with extraordinary mechanical properties, as shown in Fig. 3a,b. For comparison, we started from single-element alloying, which increased the strength σ_y from approximately 300 MPa for the A0 base alloy to approximately 500 MPa for 3 at.% Ta and to approximately 800 MPa for 12 at.% Al. Nevertheless, the latter two alloys exhibited notably reduced ductility, particularly ε_u. By contrast, both ε_u (25%) and ε_f of the (750 °C for 1 h) HEA05 alloy were far superior, simultaneously with a drastically elevated σ_y (1.75 GPa) 6-fold over the A0 base alloy. Yet, it showed an even higher WHR at the same time, enabling a notably enhanced tensile elongation (Fig. 3a and Extended Data Fig. 7). To further testify the superiority of HEA05, another two FeNiCoAlTa alloys were prepared with somewhat reduced Al and Ta concentrations, that is, Fe₃₅Ni₂₄Co₂₈Al₁₁Ta₂ and Fe₃₅Ni₂₄Co₂₇Al_11.5Ta_2.5 alloys, containing less B2 volume fractions at approximately 8% and 11%, respectively (Fig. 3 and Supplementary Fig. 8). They have lower σ_y but larger ε_u. Notably, we tuned the processing condition of our HEA05 alloy at its fixed composition and observed a range of tensile stress–strain curves (compiled in Extended Data Fig. 7), all showing significant strain hardening and large ε_u at high σ_y between 1.5 and 1.95 GPa. As summarized in Fig. 3d,e), the systematic data (elliptical area covering the data points represented by red stars) demonstrate the tunability and trend of performance, ranging from 1.5 GPa (31%) to 1.95 GPa (15%). Taken as a group, the entire ellipse presented strength–ductility combinations superior to all previous alloys.

a, Engineering stress–strain curve. b, True stress–strain curve of the HEA05 alloy (750 °C for 1 h) compared with its base alloy A0 (Fe₄₁Ni₃₄Co₂₅), with (Fe₃₅Ni₂₉Co₂₁)₈₈Al₁₂, (Fe₃₅Ni₂₉Co₂₁)₉₇Ta₃, Fe₃₅Ni₂₄Co₂₇Al_11.5Ta_2.5 (light blue) and Fe₃₅Ni₂₄Co₂₈Al₁₁Ta₂ (pink). c, Comparison of WHRs Θ with some 2-GPa steels^2,3 and 2-GPa HMEAs^19,20. (The alloys inside the light purple colours in d and e have serrated WHR curves.) d, Comparison with representatives of other high-strength alloy categories in yield strength and uniform elongation space. Our new alloys in the oval area (for the tensile curves of HEA05 processed under different conditions, see Extended Data Fig. 7 and Extended Data Table 1) clearly stood out, outperforming all previous alloys. e, Strength σ_y versus the product of σ_UTS and ε_f of HEA05 alloys, showing that the latter also outranked other ultra-high-strength FCC HEAs strengthened by L1₂ (refs. ^{18,27,28,42,50}); B2 (refs. ^15,21,30); D0₂₂ (ref. ³⁴); L1₂ and B2 (refs. ^{14,16,31,32,33}); L1₂ and LCO⁴; cryo-rolled HEAs¹⁹; lamellar HEAs²⁰; DPEL^29,35; single phase (SP)^5,36,37,38; BCC-M/HEAs^39,40,41; Fe-based, Co-based and Ni-based superalloys¹²; D&P steels²; quenched and partitioned (Q&P) steels^11,43; precipitation hardened (PH) steels²⁵; TRIP steels²⁵; and PH–TRIP steels²⁵.

This oval-shaped new territory is centred around the impressive point reported in Fig. 3a, which shows a σ_y = 1,750 ± 50 MPa, σ_UTS = 2,403 ± 46 MPa, stable WHR Θ higher than 2 GPa across the entire strain range and ε_u = 25 ± 1.5%. This combination stood out when compared with the best of bulk steels^1,2,3,10,25 (Fig. 3c–e). The simultaneous ultra-high σ_y and large ɛ_u also set this HEA05 alloy apart (comparisons in Fig. 3d) from all previously reported precipitation-strengthened HEAs^{15,16,18,26,27,28,29,30,31,32,33,34}, dual-phase eutectic lamellae (DPEL) HEAs^16,29,35,36, single-phase HEAs^5,36,37,38 and the best-performing BCC-HMEAs^39,40,41, which have either lower strength or lower ductility (or both lower).

Figure 3b shows the tensile true stress–strain curves, showing that the HEA05 alloy can reach true stress as high as approximately 3 GPa. This is because of its superior WHR, clearly above the base A0, (Fe₃₅Ni₂₉Co₂₁)₈₈Al₁₂ and (Fe₃₅Ni₂₉Co₂₁)₉₇Ta₃ alloys. The work hardening capability, in terms of the strength difference σ_UTS − σ_y = 650 MPa or the yield ratio σ_y/σ_UTS = 0.73, is extraordinary. Finally, the HEA05 alloys (red stars) also have a high value of the product σ_UTS × ε_f (for example, 60 GPa %), outranking other high-performance alloys (Fig. 3e; the way to go is in the direction pointing towards the upper-right corner), including precipitation-strengthened L1₂ (refs. ^18,27,28,42), B2 (refs. ^15,21,30), D0₂₂ (ref. ³⁴), L1₂ and B2 (refs. ^{14,16,31,32,33}), L1₂ and LCO⁴. Their performance also surpassed that of cryo-rolled HEAs¹⁹; lamellar HEAs²⁰; DPEL^29,35; single phase^5,36,37,38; Fe-based, Co-based and Ni-based superalloys¹²; D&P steels²; quenched and partitioned steels^11,43; precipitation hardened steels²⁵; transformation-induced plasticity (TRIP) steels²⁵; and precipitation hardened–transformation-induced plasticity (PH–TRIP) steels²⁵.

Note that to avoid violating the Considère instability criterion to maintain uniform tensile elongation, the WHR must always remain higher than the flow stress in the tensile test. In Fig. 3c, the previous approximately 2-GPa HEAs and steels that came close to HEA05 in WHR all exhibited stress serrations and plunges in the WHR curve to below the true stress–strain curve of HEA05, as seen superimposed using a dashed curve. Thus, these alloys suffer from unstable plastic flow and hence are placed in the dashed circle in Fig. 3d,e. In other words, they would succumb to strain localization at some point soon after yielding, and HEA05 is the only alloy with consistently stable WHRs Θ higher than 2 GPa across a wide strain range. Similarly, a high WHR was observed for HEA05 processed under other conditions (Extended Data Fig. 7c). Notably, the impressive Θ and ε_u ensured high processibility in shaping/forming and a large safety margin against fracture for our high-strength alloys, which is highly desirable for engineering applications.

In what follows, we illustrate the underlying mechanisms for the high strength and extraordinary work hardening capability. Coherent strengthening by the L1₂-type precipitates has been extensively investigated in Ni-based superalloys and HMEAs. The HEA05 combines, in one alloy, the following three desirable attributes: (1) the coherent L1₂ nanoprecipitates are effectively strengthened using Ta alloying, and their volume fraction is close to the highest ever for superalloys (such as René N5); (2) with our significant Al addition, the B2 phase fraction is also rather high among the reported HEAs; and (3) the MCIPs in our alloys contain a high level of extra elements and are, therefore, far more ductile and strain-hardenable than traditional intermetallic compounds^44,45 (further discussion later).

First, we discuss the ultra-high yield strength. This results from the densely populated L1₂ nano-MCIPs and B2 micro-MCIPs in an effectively solid solution-strengthened FCC matrix (Supplementary Fig. 9 and Supplementary Note 4). The volume fraction of precipitates in our alloy was extraordinarily high for both L1₂ (approximately 67%) and B2 (approximately 15%). The precipitate hardening in the coherent FCC/L1₂ case is mainly attributable to the γ_APB cost for the step creation by the interface-crossing dislocation, particularly for the Ta-alloyed L1₂ nano-MCIPs that have a higher γ_APB than the base L1₂ and Ti-alloyed ones (Extended Data Fig. 1). In the FCC/B2 case, the incoherent interfaces are strong traps for glide dislocations and thus are effective barriers for slip transmission. As expected, the calculation of yield strength (Supplementary Note 5) revealed that coherent L1₂ nano-MCIPs dominated the σ_y enhancement (approximately 859 MPa), followed by incoherent B2 micro-MCIPs (approximately 351 MPa), lattice friction (approximately 277 MPa), stored dislocations (approximately 206 MPa) and grain boundaries (approximately 167 MPa).

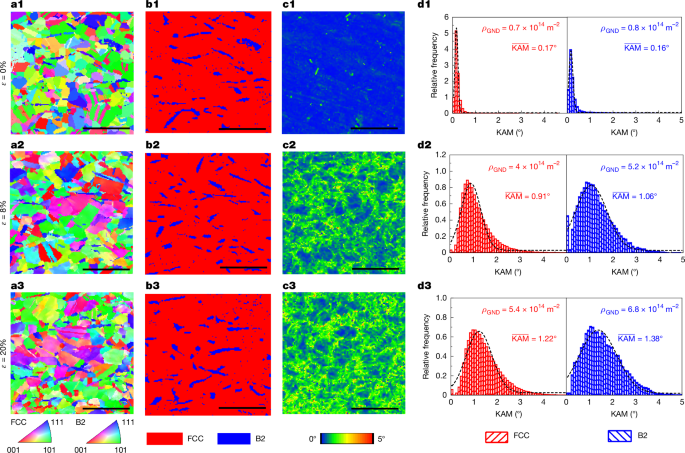
Next, we explain the extraordinary work hardening that sustains the large ε_u upon uniaxial tensile loading, as shown in Fig. 3. The dislocation densities of HEA05 at different deformation stages were monitored using a transmission electron microscope (TEM) (Fig. 2a,b and Extended Data Fig. 8), transmission Kikuchi diffraction (TKD; Extended Data Fig. 9) and electron backscatter diffraction (EBSD; Fig. 4). After 5% strain, the L1₂ nano-MCIPs were sheared by gliding dislocations, as shown in Fig. 2. (Some were observed at the FCC/L1₂ and FCC/B2 interfaces). Figure 4c(1–3),d(1–3) shows that as the strain increased from 8% to 20%, the kernel average misorientation (KAM) value of L1₂ in the FCC regions increased slightly from 0.91° to 1.22°, whereas that of B2-MCIPs increased from 1.06° to 1.38°. This indicates that the geometrically necessary dislocation (GND, ρ_GND) density increased with increasing plastic strains (Supplementary Note 6). The GND density ratio of the L1₂-dominant FCC to the B2 phase monotonically decreased from 0.87 at 0% strain to 0.79 at 20% strain (Fig. 4d(1–3)). The TKD results also revealed that both phases contained abundant GNDs with KAM less than 2° (Extended Data Fig. 9). TEM also revealed abundant dislocations accumulated inside B2-MICPs (Extended Data Fig. 8), indicating their heavy involvement in co-deformation. This is different from the traditional hard B2 phase, which often shows brittle fracture at low strain levels¹⁰. The high ρ_GND accumulated in B2 during tensile straining (note that in Fig. 4d(3), ρ_GND in B2-MCIPs is higher than that in the L1₂ + FCC; Extended Data Figs. 8 and 9) led to strain hardening along with tensile straining. This emphasizes that these B2-MCIPs are not only shearable by dislocations but also amenable to dislocation multiplication inside. This striking ductile behaviour of B2 can be attributed to its significantly depressed chemical ordering energy (Extended Data Fig. 1) and reduction in dislocation strain energy (caused by the FCC–B2 modulus mismatch when the dislocations transmitted across their incoherent interfaces^46,47; Supplementary Note 2). Although the binary NiAl B2 phase has a high γ_APB of approximately 671 mJ m⁻², alloying (particularly with Ta) into B2 reduces this γ_APB by approximately 30% (ref. ⁴⁸), rendering the intermetallic deformable through dislocations and yet still strong. Meanwhile, the strength differences between the L1₂, B2 and FCC matrices would promote non-homogeneous deformation, adding GNDs that enhance WHRs. This mechanism has recently been recast as hetero-deformation-induced (HDI) hardening (Supplementary Fig. 10)⁴⁹. The unusually heterogeneous microstructure in our complex alloy, with hierarchical inhomogeneities including interfaces on ultrafine to nanometre scales, would give rise to extra strain hardening³⁹. Given our extraordinarily high densities of precipitates, dislocation trapping/tangling, reactions and multiplication are expected to be more effective than those in previous alloys. Furthermore, the interphase interfaces serve as sustainable dislocation sources at high stress.

a–d, Inverse pole figure map (a1–a3), phase map (b1–b3), KAM map (c1–c3) and KAM plot of both the FCC (including the dominant L1₂) and B2 phases along with the estimated ρ_GND (d1–d3) at 0%, 8% and 20% tensile strains, respectively. Scale bars, 20 μm (a(1–3),b(1–3),c(1–3)).

In conclusion, we developed a high-entropy alloy (Fe₃₅Ni₂₉Co₂₁Al₁₂Ta₃), assisted by domain knowledge-guided machine learning. The new alloy has a highly heterogeneous microstructure that comprises unusually dense MCIPs in an HEA FCC matrix, including both coherent L1₂ nanoprecipitates and incoherent lower-modulus-yet-hard B2 particles, which not only effectively impart strengthening, but also profusely interact with dislocations to sustain a high WHR above 2 GPa to large true strains. The appreciable volume fraction of the ductile B2-MCIPs with effective dislocation accumulation adds room for strain hardening. Our HEAs, with a yield strength of 2 GPa, rival super steels and yet have excellent uniform ductility towards the level of elemental metals, thus go beyond what the best bulk steels have to offer. Our alloy design strategy, through active learning-guided heavy alloying and extraordinary amounts of precipitates, including ductile (and work-hardenable) second phase, is expected to be applicable to other alloy systems. This pushes the envelope of mechanical properties (towards the upper-right corner of the strength–ductility space) and expands the material selection repertoire for demanding applications.

Machine learning model for alloy design

Practically, it is impossible to search through the approximately 10⁴⁹potential alloy variants by means of trial and error. To pave the way for landing effective HEAs that outperform advanced steels, our strategy is to speed up the search by integrating active learning, a subfield of machine learning, with domain expert knowledge in microstructure design. Although active learning has been extensively used to optimize the chemical compositions of new alloys, its application in the design of microstructures has been limited by the scarcity of data available for microstructural information. To overcome this obstacle, our active learning loop was coupled with domain knowledge by customizing the principal elements and their composition ranges after each iteration, followed by the design of a triple-phase structure through post-processing once the chemical composition was optimized. The selection of elements, integration of physical features and filtering to focus on FCC alloys through the valence electron concentration all contribute to the effectiveness of our active learning process. The detailed machine learning model of the target alloy design is presented in Supplementary Note 1.

Fabrication of materials

Alloy ingots with compositions predicted from the machine learning model were prepared using the arc melting technique under a high-purity argon atmosphere. The purity of each element was at least 99.95%, and the ingot was remelted five times to ensure chemical homogeneity. The as-cast ingots were then subjected to homogenization treatment at 1,250 °C for 2 h, followed by water quenching. Subsequently, the homogenized samples were cold-rolled to a sheet with a thickness reduction of approximately 81%, recrystallized at 1,100 °C for approximately 1 min and finally aged at 750 °C for 1 h (Supplementary Fig. 5).

Microstructural characterization

The microstructures of the fabricated alloys were characterized using X-ray diffraction (XRD; Bruker D8 DISCOVER powder), TEM (JEOL JEM-2100F), scanning electron microscope (SEM; ZEISS Super 55) and EBSD installed on the equippment with energy dispersive spectroscopy. EBSD analysis along the normal direction with a step size of 0.5 μm was performed to estimate the mean grain size (d), crystallographic orientations and KAM. The TKD technique was also performed on the alloys before and after deformation using a ZEISS ULTRA plus Field Emission Gun Scanning Electron Microscope operating at 30 kV, equipped with an Oxford Instruments Channel 5 EBSD system and Nordlys-S EBSD detector. The step size used for data collection was 20 nm. All TKD scans were taken in the normal direction, parallel to the z axis. The TKD samples were prepared for electron transparency (about 100 nm) through electropolishing (Struers TenuPol-5 Twin Jet Electro-polisher) in an electrolyte solution containing 25% nitric acid and 75% methanol at −10 °C.

To analyse the distribution of elements and the sizes of nanoprecipitates in our designed FeNiCoAlTa alloys, needle-shaped specimens required for APT were fabricated by lift-outs and annular milling in an FEI Scios focused ion beam/scanning electron microscope. The APT experiments were performed on a CAMECA local electrode atom probe (LEAP 4000X Si) under high vacuum (less than 4 × 10⁻¹¹ torr) at 50 K. The Integrated Visualization & Analysis Software v.3.6.8 was used for the three-dimensional reconstructions and compositional analyses of the APT data. To determine the composition of the L1₂ nanoprecipitates, all of which had sizes less than or equal to 22 nm, the APT data were sorted for various sizes (three to five measurements at each size), and an alloy average was extracted from the 27 data points (for example, for Ta in Supplementary Fig. 11).

To obtain the precipitate volume fraction at the macroscale, synchrotron-based SAXS was conducted on the BL16B1 beamline at the Shanghai Synchrotron Radiation Facility. The sample was electrical discharge machined and wet polished to a thickness of 15 μm. Two-dimensional (2D) SAXS patterns were collected using a PILATUS 2M Detector System (1,475 × 1,679 pixels with 172 × 172 μm² pixel⁻¹), and the X-ray energy was 16 ± 1.6 keV with a beam size of 500 × 500 μm². The exposure time was 200 s. The sample-to-detector distance was calibrated to be 1,955 mm using a standard sample of silver behenate (AgBH). Background scattering from the air and sample chamber was recorded and used to correct the 2D SAXS patterns of the sample. The 2D patterns were exported and converted into one-dimensional diffraction intensity profiles as a function of the wavevector Q using the FIT2D software (v.18; ref. ⁵¹). The precipitate size distributions were obtained by fitting the Schulz–Zimm, gamma and generalized exponential distributions using the SASfit program⁵². The precipitate size and volume fraction were calculated from local monodisperse approximation⁵³, a common approximation suitable for a polydisperse system with relatively large polydispersity and high concentrations. The L1₂ volume fraction was taken as the average of the three results from these three distributions.

Tensile testing and load–unload–reload testing

To determine the strength and ductility of the designed alloys, uniaxial tensile tests were conducted at room temperature using an Instron 1195 and SUNS-UTM5105-G testing machine at a tensile strain rate of 1 × 10⁻³ s⁻¹ using a mechanical extensometer. Flat dog bone-shaped tensile specimens with a thickness of 1.5 mm and a gauge section of 15 × 4.5 mm were machined from the centre region of the plates along the rolling direction to avoid the surface effect on the microstructure. At least three samples were tested to ensure repeatability of our testing. The tensile properties, including yield strength (σ_y), ultimate tensile strength (σ_UTS), uniform elongation (ε_u) and elongation to fracture (ε_f), were recorded. HDI strengthening can be experimentally measured through the load–unload–reload test. The analysis of the load–unload–reload behaviour of our HEA05 alloy is shown in Supplementary Fig. 10a, and the HDI stress σ_HDI was quantitatively evaluated following previous studies^5,36,37,38. It seems that the stress σ_HDI in the HEA05 alloys increased with increasing strain (Supplementary Fig. 10b).

All data supporting the findings of this study are available in the paper and the Supplementary Information. The dataset used for training the machine learning model in this study are available at GitHub (https://github.com/diegoxue/Active-learning-for-Record-Setting-Alloy).

Authors and Affiliations

1. State Key Laboratory for Mechanical Behavior of Materials, Xi’an Jiaotong University, Xi’an, People’s Republic of China

   Yasir Sohail, Chongle Zhang, Dezhen Xue, Jinyu Zhang, Dongdong Zhang, Shaohua Gao, Yang Yang, Xiaoxuan Fan, Hang Zhang, Gang Liu, Jun Sun & En Ma

Contributions

J.Z. and E.M. conceived and supervised the study. J.S. and E.M. guided the project. D.X. guided the machine learning design. Y.S. performed the machine learning, alloy fabrication, microstructural analysis, mechanical properties evaluation, and data analysis. C.Z. performed the APT and TEM tests. S.G. performed the synchrotron-based SAXS test. Y.Y. performed the density funtional theory calculations. Y.S., J.Z. and E.M. wrote the paper, incorporating inputs from D.X., G.L., Y.Y., D.Z., H.Z. and X.F. All the authors contributed to the discussion of the results.

Corresponding authors

Correspondence to Jinyu Zhang, Jun Sun or En Ma.

Competing interests

The authors declare no competing interests.

Peer review information

Nature thanks Dieter Isheim and Ying Yang for their contribution to the peer review of this work.

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions