评估机器学习水晶稳定性预测的框架

评估，基准测试以及应用机器学习快速演变（ML）模型的挑战是在科学领域中常见的。具体而言，缺乏约定的任务和数据集可能会掩盖模型的性能，从而使比较变得困难。材料科学就是这样的领域，在过去的十年中，ML出版物和相关模型的数量急剧增加。与其他领域相似，例如药物发现和蛋白质设计，最终成功通常与发现具有特定功能的新材料有关。从组合意义上讲，材料科学可以看作是混合和布置不同原子与优点功能的优化问题，可捕获出现的复杂属性范围。迄今为止，〜10⁵组合已通过实验测试^{1，，，，2}，〜10⁷已经模拟了^{3，，，，4，，，，5，，，，6，，，，7}超过〜1010^{电负性和电荷平衡规则允许可能的第四纪材料}8^。Quinternies及更高的空间的探索较少，留下了许多潜在有用的材料。新材料的发现是技术进步的关键驱动力，是通往更高效的太阳能电池，更轻，更长的电池以及更小，更有效的晶体管门的道路，仅举几例。鉴于我们的可持续性目标，这些进步不能足够快。任何加速的新发现方法都应最大程度地利用。

尽管理论和方法方面取得了进步，但计算材料发现仍在提出了显着的挑战。该过程通常需要进行广泛的高通量计算，这可以在计算上进行密集且耗时。此外，结构和性质之间的复杂关系意味着找到具有期望特征的材料通常比科学更重要。ML方法通过有效识别大型数据集中的模式提供了有希望的替代方案。这些方法在处理多维数据时表现出色，平衡多个优化目标⁹，量化预测不确定性^{10，，，，11，，，，12}并从稀疏或嘈杂数据中提取有意义的信息^{13，，，，14}。这些功能使ML成为材料科学传统计算方法的互补工具特别有价值。

特别是，我们专注于ML在材料发现管道中加速使用Kohn假模式功能理论（DFT）的作用。与其他仿真框架相比，DFT在忠诚度和成本之间提供了令人信服的折衷方案，这将其作为计算材料科学界用作主力的方法。DFT作为一种方法的巨大优势使它在英国的Archer2 tier 1超级计算机中要求多达45％的核心小时¹⁵国家能源研究科学计算中心的材料科学领域的分配时间超过70％^{16，，，，17}。这种大量资源要求促使人们对减少或减轻其计算负担的方式的需求，例如提高效率或替代ML方法。

尽管通常表现出较低的精度和可靠性，但ML模型的产生速度明显比从头算模拟更快。这种速度优势将它们定位为高通量筛查活动的理想选择，在该活动中，它们可以充当计算苛刻，更高效率方法（例如DFT）的有效预过滤器。Behler和Parrinello的开创性工作¹⁸证明了使用神经网络来学习DFT势能表面（PES）。这一突破促进了快速的进步和广泛的努力，以培训越来越复杂的ML模型对可用的PES数据。早期申请通常涉及将这些模型部署为专注于特定材料的原子间潜力（或力场），这是为每个正在调查的系统创建定制培训数据集的过程^{19，，，，20}。由于材料项目（MP）等计划已经出现了更大，更多样化的数据集³，天空⁵或开放量子材料数据库⁴研究人员已经开始培训所谓的通用模型，这些模型涵盖了元素周期表中90个或更多最重要的元素。这打开了ML引导的材料发现的前景，以提高稳定晶体的命中率并加快DFT和专家驱动的搜索。

材料中ML的进度通常是根据标准基准数据集的性能测量的。随着ML模型的复杂性和适用性的增长，基准数据集需要随着它们的形式增长，以准确测量其实用性。但是，由于该领域的快速速度以及构建发现问题的各种可能方法，因此尚无大规模基准测量ML加速材料发现的能力。结果，目前尚不清楚哪些方法或模型最适合此任务。材料社区探索了几种计算发现方法，包括无坐标的预测指标，这些预测指标无需精确的原子位置¹¹，基于贝叶斯原理的顺序优化方法²¹以及具有通用元素覆盖范围的物理知识间潜力^{22，，，，23，，，，24}。尽管每种方法在特定环境中都表现出成功，但缺乏跨方法的系统比较，从而阻止了对材料发现最佳方法的明确鉴定。我们的工作旨在通过提出一个评估框架来确定最先进的模型，该框架紧密模拟了由ML模型指导的现实世界发现活动。我们的分析表明，普遍的原子间电位（UIP）超过了我们在准确性和鲁棒性方面评估的所有其他方法。

我们希望创建基准之遵循此框架的基准会创建一个途径，跨学科的研究人员具有有限的材料科学背景可以用来对相关任务进行建筑和方法论开发的建模，从而有助于材料科学方面的进步。这项工作扩展了J.R.的博士学位论文的初步研究²⁵。

这项工作提出了一项基准任务，旨在解决四个基本挑战，我们认为这对于证明实验验证ML预测的努力至关重要：

1. （1）

   预期基准测试：理想化和过度简化的基准可能无法充分捕捉实际应用中遇到的挑战。选择不合适的目标可能会出现这种断开连接¹⁴或使用非代表性数据拆分^{26，，，，27}。对于材料属性的小型数据集，删除数据拆分策略通常用于评估模型性能^{28，，，，29，，，，30}。但是，在我们的目标域中，大量的不同数据（〜10）⁵）可用，因此基于聚类的回顾性分裂策略最终可以测试人工或不代表性用例。这鼓励使用前瞻性生成的测试数据的新来源了解应用程序性能。采用这一原则，应使用预期的发现工作流程来生成测试数据，从而导致培训和测试分布之间实质但现实的协变量转移，这使得在同一发现工作流的附加应用方面可以更好地指示性能。

2. （2）

   相关目标：对于材料发现，高通量DFT形成能被广泛用作回归目标，但并不直接表明热力学稳定性或合成性。材料的真正稳定性取决于其在同一化学系统中与其他阶段的能量竞争，该竞争是由凸出船体相图的距离量化的。该距离是标准条件下（元）稳定性的主要指标³¹，尽管其他因素（例如动力学和熵稳定）会影响现实世界的稳定性，但模拟更昂贵，尤其是在规模上，它使其成为更合适的目标。此外，由于输入而需要放松结构的ML模型，其旨在加速的DFT计算产生了循环依赖性，从而降低了其实际实用性。

3. （3）

   信息指标：全局指标，例如平均绝对错误（MAE），均方根误差（RMSE）和r2^{可能会使从业者对模型可靠性具有误导性的信心。}即使具有强大回归性能的模型，当名义上准确的估计值接近决策范围时，可能会产生出乎意料的假阳性预测率，从而通过浪费的实验室资源和时间导致大量机会成本。因此，应根据其促进正确决策模式而不是仅回归准确性的能力来评估模型。一种有效的方法是定义选择标准并主要通过其分类性能评估回归模型。

4. （4）

   可伸缩性：未来的材料发现工作可能针对广泛的化学空间和大型数据制度。小型基准可能缺乏化学多样性，并且使缩放关系差或分布较弱的性能混淆。例如，随机森林在小数据集上取得了出色的性能，但由于表示学习的好处，大型数据集上的神经网络通常优于神经网络³²。尽管我们提出要充分区分模型在较大数据制度中学习的能力的必要大型训练集，但鉴于尚待探索的材料的配置空间的巨大尺寸，我们还建议构建一个任务，其中构建一个任务大于训练集大于训练集以大规模模仿真实部署的训练集。没有其他无机材料以这种方式测试大规模部署的前景。

我们重点介绍了两项特定的基准测试工作，这些努力部分解决了上述挑战：MATBENCH³³和开放催化剂项目（OCP）³⁴。其他有价值的努力，例如matsciml³⁵和Jarvis-Leaderboard³⁶汇总了各种材料与科学相关的基准任务，包括来自MATBENCH和OCP，但不会向MATBENCH或OCP中看到的设计模式引入不同的基准设计模式。

通过提供13个数据集的标准化集合，大小从DFT和实验来源提供〜300至〜132,000个样本，MATBENCH解决了可伸缩性挑战，突出了模型性能如何随数据状态的函数而变化。MATBENCH有助于将ML领域集中在材料上，增加了跨论文的可比性，并提供了对该领域进步的定量度量。重要的是，所有任务都与已知材料的特性有关。我们认为，通过要求材料稳定性预测未经保证结构的材料稳定性预测在这里是一件遗漏的任务。

OCP是一项大规模计划，旨在发现可以催化关键工业反应的底物吸附物组合，将这些吸附物转变为更有用的产品。到目前为止，OCP已发布了两个数据集OCP20（参考文献。³⁴）和OCP22（参考。³⁷），用于培训和基准测试ML模型。OCP当然解决了挑战1的挑战1，最近表明，尽管没有达到目标准确性以完全替换DFT，但使用ML与确认性DFT计算相结合，大大加快了组合筛选工作流程的速度³⁸。OCP背后的团队有第二个计划的旨在直接捕获的材料，称为OpenDac，该材料共享了ODAC23数据集³⁹。OPENDAC基准测试与OCP相同。

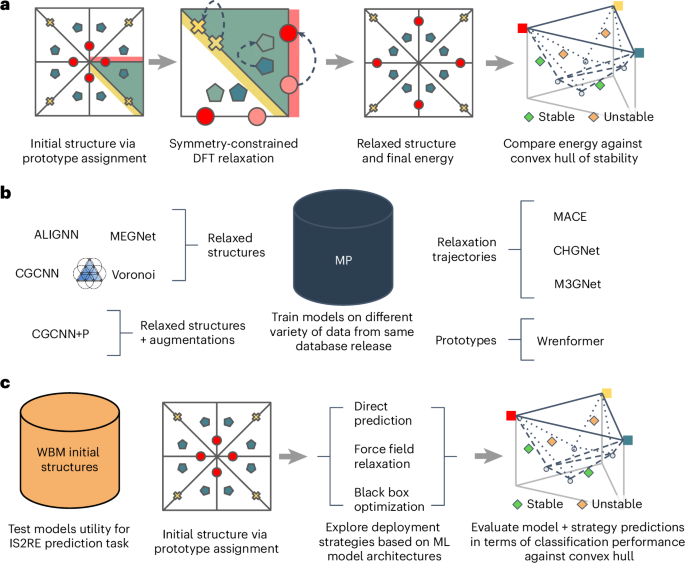
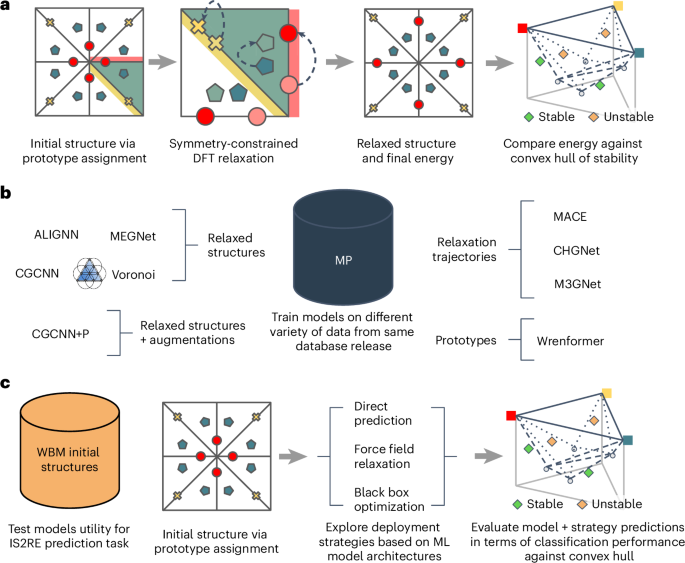
我们认为，应对这四个挑战将导致基准，从而使未来的ML引导的发现努力自信地选择适当的模型和方法来扩展计算材料数据库。数字1概述了我们建议的MATBENCH发现框架中如何使用数据。

，一种基于原型的原型发现工作流程，其中使用了已知原型中的站点的不同元素分配来创建候选结构。使用DFT将该候选者放松，以达到可以与参考凸船体进行比较的放松结构。这种工作流程用于构建WBM数据集。b，诸如MP之类的数据库提供了丰富的数据集，不同的学术组已用来探索不同类型的模型。虽然早期的工作倾向于专注于各个模式，但我们的框架可以跨模态进行一致的模型比较。c，最终用户采用ML模型并使用它来预测初始结构（IS2RE）的放松能量的提议的测试评估框架。然后，该能量用于预测材料相对于参考凸壳的稳定还是不稳定。从应用程序的角度来看，此分类性能与筛选工作流程中的预期用例更好地一致。

桌子1显示了MATBENCH发现的初始版本中包含的所有模型的性能指标，该模型报告了独特的原始结构子集。Equibormerv2+dens在ML引导的材料发现中的性能最高，超过了九个报告的指标的所有其他模型。当计算缺失值或明显病理预测的指标（每个原子或更高的误差）时，我们将虚拟回归值分配给这些点。发现加速度因子（DAF）量化了模型与测试集的随机选择相比，模型在寻找稳定结构方面的有效性更高。正式地，DAF是精度与患病率的比率。最大可能的DAF是流行率的倒数，在我们的数据集上是（33,000/215,000）¹6.5。因此，EquibrounServ2+dens实现的5.04的最新目前为改进留出了空间。但是，在10,000个材料的子集上评估每个模型的每个模型都排名最稳定（补充表2），对于equibroSulerv2â+dens，我们看到了令人印象深刻的DAF，这是该任务的最佳性能。表1在我们基准中测试的所有模型的分类和回归指标。f

f1_{，DAF），他们的回归性能（}r2^{，rmse）较差。}值得注意的是，仅能量模型中只有Alignn，Bowsr和CGCNN+P实现了积极的确定系数（r2^）。消极的r²均值模型预测解释了数据中观察到的变化，而不是简单地预测测试集的平均值。换句话说，这些模型在全球意义上（在整个数据集范围内）并非可预测。然而，具有负面的模型r²可能仍然显示出远离稳定性阈值的材料的预测能力（即分配尾巴中）。它们的性能最接近每个原子稳定阈值的0 eV，材料浓度最高。这说明了使用的限制r²单独评估用于分类任务的模型，例如稳定性预测。

CGCNN+P的原因比CGCNN获得了更好的回归指标，但由于分类器从补充图中显而易见，因此仍然更糟。5通过指出CGCNN+P直方图在0船体距离稳定性阈值下更加明显。这甚至导致预测的凸面距离的小错误足以倒入分类。同样，这是可以仔细选择要优化的指标的证据。在评估能量预测时，回归指标更为普遍。但是，我们的基准测试将能量预测视为仅意味着对复合稳定性进行分类的终止。回归准确性的提高对材料发现的用途有限，除非它们也提高了分类精度。我们的结果表明，这不是给定的。

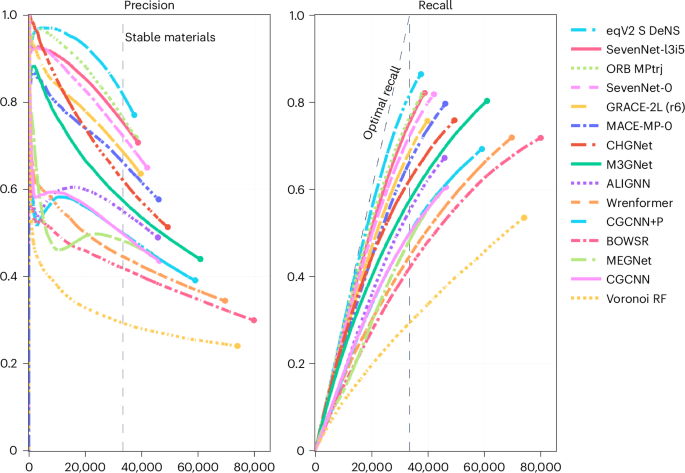
数字2显示模型按模型预测的船体距离从大多数稳定到最不稳定的材料进行排名：最低的材料在顶部的船体以下，底部的材料就在船体位于底部的材料。对于每个模型，我们遍历该列表，并在每个步骤中计算正确识别的稳定材料的精度和回忆。这完全模拟了这些模型如何在潜在材料发现活动中使用，并揭示了模型的性能如何随发现活动长度的函数而变化。作为从业者，您通常有一定数量的资源来验证模型预测。这些曲线使您可以读取这些限制的最佳模型。例如，以这种方式绘制结果表明，CHGNET最初比equibroumenterv2â+dens，orb mptrj，七网和梅斯等模型获得更高的精度，这些模型在整个测试集中报告了更高的精度。

典型的发现运动将按照模型预测的船体距离从大多数稳定到最不稳定的距离进行对假设材料进行排名，并首先验证最稳定的预测。正确的稳定预测的较高部分对应于更高的精度，而较少的稳定材料则对应于更高的回忆。精度仅基于到达所选的材料，而累积召回取决于知道预期的阳性总数。诸如EQV2 S dens和Orb MPTRJ之类的模型在详尽的发现活动中的表现更好（筛选候选池的份额更高）；在验证预测最稳定的较小比例的材料时，例如CHGNET等其他人会做得更好。UIPS在较短的20,000材料较少或更少的材料中提供了明显提高的精度，因为它们不太容易发生高度稳定的材料中的假阳性预测。

在图中2当该模型认为MP凸壳以下的Wang-Botti-Marques（WBM）测试集中没有更多材料时，每条线将终止。虚线的垂直线显示了我们测试集中稳定结构的实际数量。所有模型在某种程度上都偏向于稳定性，因为它们都高估了这个数字，大多数BOWSR中的大部分都达到了133％。高估的主要影响旨在验证所有预测为稳定的材料的详尽发现活动。实际上，运动通常是有限的（例如，到10,000 dft放松身心）。通过通过预测稳定性和仅验证预算决定的最高分数来对候选人进行排名，避免在较不稳定的预测中发现的较高的假阳性集中度，而不会降低广告系列的有效发现率（请参阅补充表2即使是最差的表现模型的DAF，Voronoi RF也从1.58跳到2.49）。

在图2中的召回图上的对角线最佳召回线。2如果一个模型从未做出假阴性预测并停止在达到稳定材料的真实数量时，就可以实现稳定的晶体。在检查UIP模型时，我们发现它们都达到了相似的召回值，范围约为0.75至0.86。这显着比我们在同一模型的精确度中看到的变化要小，〜0.44 0.77。检查重叠时，我们发现模型正确协议的交点在〜0.75 〜0.86范围内仅计算0.57的精度，只有0.04个示例，其中所有模型同时误导了。这些结果表明模型正在做出有意义的不同预测。

检查图2中的精确图。2，我们观察到，仅能能量的模型早期表现出更明显的下降，在前5,000种筛选材料中降至0.6或更少。这些模型中的许多（除了Bowsr，Wrenformer和Voronoi RF之外，所有模型）在其累积精度中显示出有趣的钩形，在模拟广告系列的中间再次稍微恢复了5,000和30,000个中间，然后再次下降到结束。

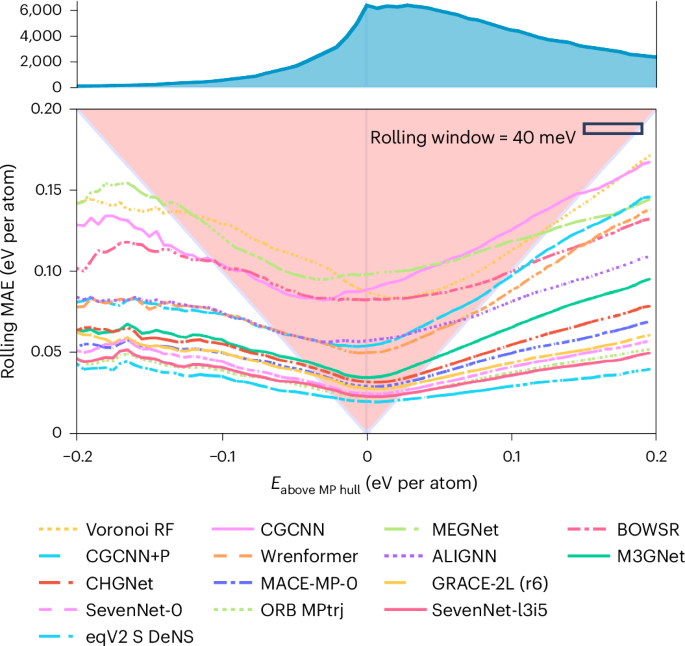
数字3提供了不同模型的可靠性的视觉表示，这是材料的DFT距离与MP凸壳的函数的函数。线条显示了模型预测的船体距离与DFT的滚动MAE。我们在危险三角形的三角形上造成的红色阴影区域强调了平均模型误差超过0 eV处稳定性阈值的区域。只要滚动的MAE保留在这个三角形内，该模型就非常容易被错误分类的结构。该区域中的平均误差大于在0处的分类阈值的距离，因此，在误差指向稳定性阈值的情况下，它足够大，可以将正确的分类转换为不正确的分类。在该区域内，平均误差幅度超过了在0 eV处的分类阈值的距离。因此，当错误指向稳定边界时，它们足够大，可以扭转正确的分类。模型的误差曲线速度越快，即将左侧的三角形（代表负DFT船体距离）退出，其错误将稳定结构分类为不稳定的趋势越低，从而降低了虚假负面因素。右侧迅速退出（正DFT船体距离）与预测不稳定结构稳定的概率降低相关，从而减少了假阳性。

这些线代表WBM测试集上的滚动MAE，这是与MP训练集凸壳的距离的函数。危险的红色三角形表示平均误差超过稳定阈值距离的区域（0 eV）。在此三角形中，由于错误可能会翻转分类，因此模型更有可能错误地分类材料。从三角形出发的早期退出与较少的假阳性（右侧）或假阴性（左侧）相关。滚动窗口的宽度表示预测错误的平均范围。

与右边缘相比，模型通常向图的左边缘显示出较低的滚动误差。这种不平衡表明，对假阳性预测的倾向比假阴性预测更大。换句话说，所有模型都不太容易预测每种dft hull距离为0.2 eV的材料，而不是预测材料为 +0.2 ev dft hull hull距离为稳定。从实际的角度来看，这是不可取的，因为与验证错误预测的稳定材料（假阳性）相关的机会成本通常高于缺少真正稳定的材料（假阴性）。我们假设这种误差不对称是由MP训练集的稳定材料比例较高的，这会导致在其上训练的统计模型偏向于将低能量分配到高能原子布置上。在具有更多高能结构的数据集上进行培训，例如Alexandria⁷和omat24（参考。⁴⁰），可以通过平衡这种偏见来提高性能。

我们已经证明了基于ML的分类在高通量材料发现中的有效性，并认为将ML纳入发现工作流的好处现在显然超过了成本。桌子1在现实的基准方案中显示，几种模型在整个数据集中达到了大于2.5的发现加速度，并且在仅考虑每个模型的10,000个最稳定的预测时（补充表）2）。最初，尚不确定加速高通量发现的最有希望的ML方法。我们的结果揭示了UIP在准确性和外推性能方面具有明显的优势。合并力信息使UIP可以更好地模拟通往DFT-Relax结构的松弛途径，从而实现更准确的最终能量测定。

通过他们的测试组排名最多f₁在热力学稳定性预测上得分，我们发现equibouserV 2>orbâ> nnet -nnetâmaceâmaceâmaceâ>chgnetâm3gnetâm3gnetâm3gnetâ> - megnetn> alignn>megnetâmegnetâ>cgcnnâ>cgcnnâ>cgcnnâ>cgcnnâ> cgcnn> cgcnn+p>指纹随机森林。顶级模型是UIP，我们确定是ML引导材料发现的最佳方法f₁与虚拟选择相比，在前10,000个最稳定的预测中，晶体稳定性分类的0.57级和最高6ã的得分为0.82。

随着凸壳通过未来的发现变得更加全面地取样，未知稳定结构的一部分将自然下降。这将导致不那么丰富的测试集，因此，更具挑战性和歧视性的发现基准。但是，此处框架的发现任务仅解决了潜在UIP应用程序的有限子集。我们认为，其他基准对于有效指导UIP开发至关重要。这些努力应优先考虑基于任务的评估框架，以解决我们确定的四个关键挑战，以缩小部署差距：采用预期的而不是回顾性基准测试，并使用信息性的指标和可扩展性来解决相关目标。

展望未来，相关文献中观察到的一贯线性日志学习曲线⁴¹表明，可以通过增加的训练数据更容易解锁UIP的误差的进一步减少。这已经在侏儒的缩放结果中得到了证实⁴²，Mettersim⁴³，亚历山大⁷和omat24（参考。⁴⁰），当在更大的数据集上培训时，所有这些都显示出表现的改善。为了实现扩展这些模型的全部潜力，未来的努力应部署其资源，以产生大量高于PBE的保真度培训数据。UIP模型的质量由其培训数据的质量和理论水平限制。

除了简单地预测0 -K的热力学稳定性外，未来模型还需要在不同的环境条件（例如有限温度和压力）下理解和预测材料特性，以帮助材料发现。In this context, temperature-dependent dynamical properties constitute an area ripe for interatomic potentials.Another key open question is how effectively these models can contribute to the computational prediction of synthesis pathways.Many current methods for predicting reaction pathways employ heuristic rules to manage the considerable complexity introduced by metastability, in addition to relying on conventional ground-state ab initio data^{44，，，，45，，，，46}。These algorithms will massively benefit from more efficient estimates of reaction energy barriers⁴⁷and non-crystalline, out-of-equilibrium materials⁴⁸, opening up a whole new field to ML-accelerated inquiry.

Matbench Discovery framework

As first presented in J.R.ʼs PhD thesis²⁵, we propose an evaluation framework that places no constraints on the type of data a model is trained on as long as it would be available to a practitioner conducting a real materials discovery campaign.This means that for the high-throughput DFT data considered, any subset of the energies, forces, stresses or any other properties that can be routinely extracted from DFT calculations, such as magnetic moments, are valid training targets.All of these would be available to a practitioner performing a real materials discovery campaign and hence are permitted for training any model submission.We enforce only that at test time, all models must make predictions on the convex hull distance of the relaxed structure with only the unrelaxed structure as input.This setup avoids circularity in the discovery process, as unrelaxed structures can be cheaply enumerated through elemental substitution methodologies and do not contain information inaccessible in a prospective discovery campaign.数字1provides a visual overview of design choices.

The convex hull distance of a relaxed structure is chosen as the measure of its thermodynamic stability, rather than the formation energy, as it informs the decision on whether to pursue a potential candidate crystal.This decision was also motivated by ref.¹⁴, which found that even composition-only models are capable of predicting DFT formation energies with useful accuracy.However, when tasking those same models with predicting decomposition enthalpy, performance deteriorated sharply.This insight exposes how ML models are much less useful than DFT for discovering new inorganic solids than would be expected given their low prediction errors for formation energies due to the impact of random as opposed to systematic errors.

Standard practice in ML benchmarks is to hold all variables fixed—most importantly the training data—and vary only the model architecture to isolate architectural effects on the performance.We deliberately deviate from this practice due to diverging objectives from common ML benchmarks.Our goal is to identify the best methodology for accelerating materials discovery.What kind of training data a model can ingest is part of its methodology.Unlike energy-only models, UIPs benefit from the additional training data provided by the forces and stresses recorded in DFT relaxations.This allows them to learn a fundamentally higher-fidelity model of the physical interactions between ions.That is a genuine advantage of the architecture and something any benchmark aiming to identify the optimal methodology for materials discovery must reflect.In light of this utilitarian perspective, our benchmark contains models trained on varying datasets, and any model that can intake more physical modalities from DFT calculations is a valid model for materials discovery.

We define the MP³v.2022.10.28 database release as the maximum allowed training set for any compliant model submission.Models may train on the complete set of relaxation frames, or any subset thereof such as the final relaxed structures.Any subsets of the energies, forces and stresses are valid training targets.In addition, any auxiliary tasks such as predicting electron densities, magnetic moments, site-partitioned charges and so on that can be extracted from the output of the DFT calculations are allowed for multi-task learning⁴⁹。Our test set consists of the unrelaxed structures in the WBM dataset⁵⁰。Their target values are the PBE formation energies of the corresponding DFT-relaxed structures.

Limitations of this framework

While the framework proposed here directly mimics a common computational materials discovery workflow, it is worth highlighting that there still exist notable limitations to these traditional computational workflows that can prevent the material candidates suggested by such a workflow from being able to be synthesized in practice.For example, high-throughput DFT calculations often use small unit cells which can lead to artificial orderings of atoms.The corresponding real material may be disordered due to entropic effects that cannot be captured in the 0-K thermodynamic convex hull approximated by DFT⁵¹。

Another issue is that, when considering small unit cells, the DFT relaxations may get trapped at dynamically unstable saddle points in the true PES.This failure can be detected by calculating the phonon spectra for materials predicted to be stable.However, the cost of doing so with DFT is often deemed prohibitive for high-throughput screening.The lack of information about the dynamic stability of nominally stable materials in the WBM test set prevents this work from considering this important criterion as an additional screening filter.However, recent progress in the development of UIPs suggests that ML approaches will soon provide sufficiently cheap approximations of these terms for high-throughput searches^{52，，，，53}。As the task presented here begins to saturate, we believe that future discovery benchmarks should extend upon the framework proposed here to also incorporate criteria based on dynamic stability.

When training UIP models there is competition between how well given models can fit the energies, forces and stresses simultaneously.The metrics in the Matbench Discovery leaderboard are skewed towards energies and consequently UIP models trained with higher weighting on energies can achieve better metrics.We caution that optimizing hyperparameters purely to improve performance on this benchmark may have unintended consequences for models intended for general purpose use.Practitioners should also consider other involved evaluation frameworks that explore orthogonal use cases when developing model architectures.We highlight work from Póta et al.⁵⁴on thermal conductivity benchmarking, Fu et al.⁵⁵on MD stability for molecular simulation and Chiang et al.⁵⁶on modelling reactivity (hydrogen combustion) and asymptotic correctness (homonuclear diatomic energy curves) as complementary evaluation tasks for assessing the performance of UIP models.

We design the benchmark considering a positive label for classification as being on or below the convex hull of the MP training set.An alternative formulation would be to say that materials in WBM that are below the MP convex hull but do not sit on the combined MP + WBM convex hull are negatives.The issue with such a design is that it involves unstable evaluation metrics.If we consider the performance against the final combined convex hull rather than the initial MP convex hull, then each additional sample considered can retroactively change whether or not a previous candidate would be labelled as a success as it may no-longer sit on the hull.Since constructing the convex hull is computationally expensive, this path dependence makes it impractical to evaluate cumulative precision metrics (Fig.2）。The chosen setup does increase the number of positive labels and could consequently be interpreted as overestimating the performance.This overestimation decreases as the convex hull becomes better sampled.Future benchmarks building on this work could make use of the combination of MP + WBM to control this artefact.An alternative framework could report metrics for each WBM batch in turn and retrain between batches;this approach was undesirable here as it increases the cost of submission fivefold and introduces many complexities, for example, should each model only retrain on candidates it believed to be positive, that would make fair comparison harder.

数据集

MP training set

The MP is a widely used database of inorganic materials properties that have been calculated using high-throughput ab initio methods.At the time of writing, the MP database³has grown to ~154,000 crystals, covering diverse chemistries and providing relaxed and initial structures as well as the relaxation trajectory for every entry.

Our benchmark defines the training set as all data available from the v.2022.10.28 MP release.We recorded a snapshot of energies, forces, stresses and magnetic moments for all MP ionic steps on 15 March 2023 as the canonical training set for Matbench Discovery, and provide convenience functions through our Python package for easily feeding those data into future model submissions to our benchmark.

Flexibility in specifying the dataset allows authors to experiment with and fully exploit the available data.This choice is motivated by two factors.First, it may seem that models trained on multiple snapshots containing energies, forces and stresses receive more training data than models trained only on the energies of relaxed structures.However, the critical factor is that all these additional data were generated as a byproduct of the workflow to produce relaxed structures.Consequently, all models are being trained using data acquired at the same overall cost.If some architectures or approaches can leverage more of these byproduct data to make improved predictions this is a fair comparison between the two models.This approach diverges philosophically from other benchmarks such as the OCP and Matbench where it has been more common to subcategorize different models and look at multiple alternative tasks (for example, composition-only versus structure available in Matbench or IS2RS, IS2RE, S2EF in OCP) and which do not make direct comparisons of this manner.Second, recent work in the space from refs.^{57，，，，58}has claimed that much of the data in large databases such as MP are redundant and that models can be trained more effectively by taking a subset of these large data pools.From a systems-level perspective, identifying innovative cleaning or active-learning strategies to make better use of available data may be as crucial as architectural improvements, as both can similarly enhance performance, especially given the prevalence of errors in high-throughput DFT.Consequently, such strategies where they lead to improved performance should be able to be recognized within the benchmark.We encourage submissions to submit ablation studies showing how different system-level choices affect performance.Another example of a system-level choice that may impact performance is the choice of optimizer, for example, FIRE⁵⁹versus L-BFGS, in the relaxation when using UIP models.

We highlight several example datasets that are valid within the rules of the benchmark that take advantage of these freedoms.The first is the MP-crystals-2019.4.1 dataset⁶⁰, which is a subset of 133,420 crystals and their formation energies that form a subset of the v.2021.02.08 MP release.The MP-crystals-2022.10.28 dataset is introduced with this work comprising a set of 154,719 structures and their formation energies drawn from the v.2021.02.08 MP release.The next is the MPF.2021.2.8 dataset22^{curated to train the M3GNet model, which takes a subset of 62,783 materials from the v.2021.02.08 MP release.}The curators of the MPF.2021.2.8 dataset down-sampled the v.2021.02.08 release notably to select a subset of calculations that they believed to be most self-consistent.Rather than taking every ionic step from the relaxation trajectory, this dataset opts to select only the initial, final and one intermediate structure for each material to avoid biasing the dataset towards examples where more ionic steps were needed to relax the structure.Consequently the dataset consists of 188,349 structures.The MPF.2021.2.8 is a proper subset of the training data as no materials were deprecated between the v.2021.02.08 and v.2022.10.28 database releases.The final dataset we highlight, with which several of the UIP models have been trained, is the MPtrj dataset²³。This dataset was curated from the earlier v.2021.11.10 MP release.The MPtrj dataset is a proper subset of the allowed training data but several potentially anomalous examples from within MP were cleaned out of the dataset before the frames were subsampled to remove redundant frames.It is worth noting that the v.2022.10.28 release contains a small number of additional Perovskite structures not found in MPtrj that could be added to the training set within the scope of the benchmark.

We note that the v.2023.11.1 deprecated a large number of calculations so data queried from subsequent database releases are not considered valid for this benchmark.

WBM test set

The WBM dataset⁵⁰consists of 257,487 structures generated via chemical similarity-based elemental substitution of MP source structures followed by DFT relaxation and calculating each crystal’s convex hull distance.The element substitutions applied to a given source structure were determined by random sampling according to the weights in a chemical similarity matrix data-mined from the ICSD⁶¹。

The WBM authors performed five iterations of this substitution process (we refer to these steps as batches).After each step, the newly generated structures found to be thermodynamically stable after DFT relaxation flow back into the source pool to partake in the next round of substitution.This split of the data into batches of increasing substitution count is a unique and compelling feature of the test set as it allows out-of-distribution testing by examining whether model performance degrades for later batches.A higher number of elemental substitutions on average carries the structure farther away from the region of material space covered by the MP training set (see Supplementary Fig.6有关详细信息）。While this batch information makes the WBM dataset an exceptionally useful data source for examining the extrapolation performance of ML models, we look primarily at metrics that consider all batches as a single test set.

To control for the potential adverse effects of leakage between the MP training set and the WBM test set, we cleaned the WBM test set based on protostructure matching.We refer to the combination of a materials prototype and the elemental assignment of its wyckoff positions as a protostructure following ref.⁶²。First we removed 524 pathological structures in WBM based on formation energies being larger than 5 eV per atom or smaller than −5 eV per atom.We then removed from the WBM test set all examples where the final protostructure of a WBM material matched the final protostructure of an MP material.In total, 11,175 materials were cleaned using this filter.We further removed all duplicated protostructures within WBM, keeping the lowest energy structure in each instance, leaving 215,488 structures in the unique prototype test set.

Throughout this work, we define stability as being on or below the convex hull of the MP training set (e_{MP hull dist} ≤ 0).In total, 32,942 of 215,488 materials in the WBM unique prototype test set satisfy this criterion.Of these, ~33,000 are unique prototypes, meaning they have no matching structure prototype in MP nor another higher-energy duplicate prototype in WBM.Our code treats the stability threshold as a dynamic parameter, allowing for future model comparisons at different thresholds.For initial analysis in this direction, see Supplementary Fig.1。As WBM explores regions of materials space not well sampled by MP, many of the discovered materials that lie below MP’s convex hull are not stable relative to each other.Of the ~33,000 that lie below the MP convex hull less than half, or around ~20,000, remain on the joint MP + WBM convex hull.

This observation suggests that many WBM structures are repeated samples in the same new chemical spaces.It also highlights a critical aspect of this benchmark in that we knowingly operate on an incomplete convex hull.Only current knowledge of competing points on the PES is accessible to a real discovery campaign and our metrics are designed to reflect this.

型号

To test a wide variety of methodologies proposed for learning the potential energy landscape, our initial benchmark release includes 13 models.Next to each model’s name we give the training targets that were used: E, energy;F, forces;S, stresses;and M, magnetic moments.The subscripts G and D refer to whether gradient-based or direct prediction methods were used to obtain force and stress predictions.

1. （1）

   EquiformerV2 + DeNS^{63，，，，64}(EFS_d): EquiformerV2 builds on the first Equiformer model⁶⁵by replacing theso(3) convolutions with equivariant Spherical Channel Network convolutions⁶⁶as well as a range of additional tweaks to make better use of the ability to scale to higher\({L}_{\max }\)using equivariant Spherical Channel Network convolutions.EquiformerV2 uses direct force prediction rather than taking the forces as the derivative of the energy predictions for computational efficiency.Here we take the pre-trained ‘eqV2 S DeNS’⁴⁰trained on the MPtrj dataset.This model in addition to supervised training on energies, forces and stresses makes use of an auxiliary training task based on de-noising non-equilibrium structures⁶⁴。We refer to this model as ‘EquiformerV2 + DeNS’ in the text and ‘eqV2 S DeNS’ in plots.

2. （2）

   球⁶⁷(EFS_d): Orb is a lightweight model architecture developed to scale well for the simulation of large systems such as metal organic frameworks.Rather than constructing an architecture that is equivariant by default, Orb instead makes use of data augmentation during training to achieve approximate equivariance.This simplifies the architecture, allowing for faster inference.We report results for the ‘orb-mptrj-only-v2’ model, which was pre-trained using a diffusion-based task on MPtrj before supervised training on the energies, forces and stresses in MPtrj.For simplicity we refer to this model as ‘ORB MPtrj’.

3. （3）

   SevenNet⁶⁸(EFS_g): SevenNet emerged from an effort to improve the performance of message-passing neural networks⁶⁹when used to conduct large-scale simulations involving that benefit from parallelism via spatial decomposition.Here we use the pre-trained ‘SevenNet-0_11July2024’ trained on the MPtrj dataset.The SevenNet-0 model is an equivariant architecture based on a NequIP⁷⁰architecture that mostly adopts the GNoME⁴²超参数。SevenNet-0 differs from NequIP and GNoME by replacing the tensor product in the self-connection layer with a linear layer applied directly to the node features, and this reduces the number of parameters from 16.24 million in GNoME to 0.84 million for SevenNet-0.For simplicity we refer to this model as ‘SevenNet’.

4. （4）

   锤²⁴(EFS_g): MACE builds upon the recent advances^{70，，，，71}in equivariant neural network architectures by proposing an approach to computing high-body-order features efficiently via Atomic Cluster Expansion⁷²。Unlike the other UIP models considered, MACE was primarily developed for molecular dynamics of single material systems and not the universal use case studied here.The authors trained MACE on the MPtrj dataset;these models have been shared under the name ‘MACE-MP-0’ (ref.⁵²) and we report results for the ‘2023-12-03’ version commonly called ‘MACE-MP-0 (medium)’.For simplicity we refer to this model as ‘MACE’.

5. （5）

   CHGNet²³(EFS_gM): CHGNet is a UIP for charge-informed atomistic modelling.Its distinguishing feature is that it was trained to predict magnetic moments on top of energies, forces and stresses in the MPtrj dataset (which was prepared for the purposes of training CHGNet).By modelling magnetic moments, CHGNet learns to accurately represent the orbital occupancy of electrons, which allows it to predict both atomic and electronic degrees of freedom.We make use of the pre-trained ‘v.0.3.0’ CHGNet model from ref.²³。

6. （6）

   M3GNet (ref.²²) (EFS_g): M3GNet is a graph neural network (GNN)-based UIP for materials trained on up to three-body interactions in the initial, middle and final frames of MP DFT relaxations.The model takes the unrelaxed input and emulates structure relaxation before predicting energy for the pseudo-relaxed structure.We make use of the pre-trained ‘v.2022.9.20’ M3GNet model from ref.22^{trained on the compliant MPF.2021.2.8 dataset.}（7）

7. ALIGNN

   73^{(E): ALIGNN is a message-passing GNN architecture that takes as input both the interatomic bond graph and a line graph corresponding to three-body bond angles.}The ALIGNN architecture involves a global pooling operation, which means that it is ill-suited to force field applications.To address this the ALIGNN-FF model was later introduced without global pooling⁷⁴。We trained ALIGNN on the MP-crystals-2022.10.28 dataset for this benchmark.

8. （8）

   MEGNet⁶⁰(E): MEGNet is another GNN-based architecture that also updates a set of edge and global features (such as pressure and temperature) in its message-passing operation.This work showed that learned element embeddings encode periodic chemical trends and can be transfer-learned from large datasets (formation energies) to predictions on small data properties (band gaps, elastic moduli).We make use of the pre-trained ‘Eform_MP_2019’ MEGNet model trained on the compliant MP-crystals-2019.4.1 dataset.

9. （9）

   CGCNN⁷⁵(E): CGCNN was the first neural network model to directly learn eight different DFT-computed material properties from a graph representing the atoms and bonds in a periodic crystal.CGCNN was among the first to show that just as in other areas of ML, given large enough training sets, neural networks can learn embeddings that outperform human-engineered structure features directly from the data.We trained an ensemble of 10 CGCNN models on the MP-crystals-2022.10.28 dataset for this benchmark.

10. （10）

    CGCNN+P⁷⁶(E): This work proposes simple, physically motivated structure perturbations to augment stock CGCNN training data of relaxed structures with structures resembling unrelaxed ones but mapped to the same DFT final energy.Here we chosep = 5, meaning the training set is augmented with five random perturbations of each relaxed MP structure mapped to the same target energy.In contrast to all other structure-based GNNs considered in this benchmark, CGCNN+P is not attempting to learn the Born–Oppenheimer PES.The model is instead taught the PES as a step-function that maps each valley to its local minimum.The idea is that during testing on unrelaxed structures, the model will predict the energy of the nearest basin in the PES.The authors confirm this by demonstrating a lowering of the energy error on unrelaxed structures.We trained an ensemble of ten CGCNN+P models on the MP-crystals-2022.10.28 dataset for this benchmark.

11. （11）

    Wrenformer (E): For this benchmark, we introduce Wrenformer, which is a variation on the coordinate-free Wren model¹¹constructed using standard QKV-self-attention blocks⁷⁷in place of message-passing layers.This architectural adaptation reduces the memory usage, allowing the architecture to scale to structures with greater than 16 Wyckoff positions.Similar to its predecessor, Wrenformer is a fast, coordinate-free model aimed at accelerating screening campaigns where even the unrelaxed structure is a priori unknown⁶²。The key idea is that by training on the coordinate anonymized Wyckoff positions (symmetry-related positions in the crystal structure), the model learns to distinguish polymorphs while maintaining discrete and computationally enumerable inputs.The central methodological benefit of an enumerable input is that it allows users to predict the energy of all possible combinations of spacegroup and Wyckoff positions for a given composition and maximum unit cell size.The lowest-ranked protostructures can then be fed into downstream analysis or modelling.We trained an ensemble of ten Wrenformer models on the MP-crystals-2022.10.28 dataset for this benchmark.

12. （12）

    BOWSR²¹(E): BOWSR combines a symmetry-constrained Bayesian optimizer with a surrogate energy model to perform an iterative exploration–exploitation-based search of the potential energy landscape.Here we use the pre-trained ‘Eform_MP_2019’ MEGNet model⁶⁰for the energy model as proposed in the original work.The high sample count needed to explore the PES with a Bayesian optimizer makes this by far the most expensive model tested.

13. （13）

    Voronoi RF⁷⁸(E): A random forest trained to map a combination of composition-based Magpie features⁷⁹and structure-based relaxation-robust Voronoi tessellation features (effective coordination numbers, structural heterogeneity, local environment properties, …) to DFT formation energies.This fingerprint-based model predates most deep learning for materials but notably improved over earlier fingerprint-based methods such as the Coulomb matrix⁸⁰and partial radial distribution function features⁸¹。It serves as a baseline model to see how much value the learned featurization of deep learning models can extract from the increasingly large corpus of available training data.We trained Voronoi RF on the MP-crystals-2022.10.28 dataset for this benchmark.

作者和隶属关系

1. Department of Physics, University of Cambridge, Cambridge, UK

   Janosh Riebesell, Rhys E. A. Goodall & Alpha A. Lee

2. Lawrence Berkeley National Laboratory, Berkeley, CA, USA

   Janosh Riebesell, Yuan Chiang, Bowen Deng, Gerbrand Ceder, Mark Asta, Anubhav Jain & Kristin A. Persson

3. Federal Institute of Materials Research and Testing (BAM), Berlin, Germany

   Philipp Benner

4. Department of Materials Science and Engineering, University of California, Berkeley, Berkeley, CA, USA

   Yuan Chiang, Bowen Deng, Gerbrand Ceder, Mark Asta & Kristin A. Persson

贡献

J.R. was responsible for the methodology, software, data curation, investigation (training: CGCNN, CGCCN+P, Wrenformer, Voronoi RF), validation, formal analysis and writing the original draft.R.E.A.G.was responsible for conceptualization, software, validation, formal analysis, writing the original draft, and reviewing and editing the manuscript.P.B.was responsible for software, investigation (training: ALIGNN, MACE) and writing the original draft.Y.C.was responsible for investigation (training: MACE), formal analysis and reviewing and editing the manuscript.B.D.was responsible for data curation (MPtrj), investigation (training: CHGNet), and reviewing and editing the manuscript.G.C.and M.A. were responsible for supervision and funding acquisition.A.A.L.and A.J.监督项目。K.A.P.was responsible for supervision, reviewing and editing the manuscript, and funding acquisition.

相应的作者

对应Janosh Riebesell或者Kristin A. Persson。道德声明

作者没有宣称没有竞争利益。

同行评审

自然机器智能

thanks Ju Li, Logan Ward and Tian Xie for their contribution to the peer review of this work.附加信息

This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.要查看此许可证的副本，请访问http://creativecommons.org/licenses/by/4.0/。重印和权限

关于这篇文章