基于人工智能和深度学习的音乐教学改革中资源的智能产生和优化

尽管传统的音乐教学模式在一定程度上促进了学生音乐技能的发展，但个性化教学，学习进度跟踪和有效使用教学资源仍然存在一些局限性¹。随着信息技术的持续进步，尤其是人工智能（AI）技术的出现，音乐教育领域发生了重大变化。AI技术可以实现个性化的建议和自动调整，以满足学生的不同学习需求^{2，，，，3}。通过深度学习和深入学习的结合，可以构建一个更灵活和适应性的教学系统，从而为音乐教育带来前所未有的创新和突破。

深入的强化学习（DRL）是一种结合深度学习和强化学习的先进技术，具有强大的适应能力和独立的决策能力，并且可以根据复杂环境中的反馈来优化行为策略^{4，，，，5}。在音乐教学中，使用DRL技术生成和优化资源可以动态调整教学内容，学习材料和教学方法，以最大程度地提高学生的学习效果和兴趣⁶。在AI的帮助下，有一个新的解决方案解决了大规模个性化需求的问题，在传统音乐教学中很难处理。因此，本文的目的是研究基于AI-DRL的资源智能生成和优化技术，使用AI技术提高音乐指导的效率和质量，并提高教育的数字化转型。

本文的主要目标是研究基于DRL的音乐教育工具的创建和优化方法。通过使用DRL模型，该论文专门寻求实现对学生学习状态的实时反馈和适应性，并自动开发与每个学生独特需求相对应的教学材料。结果，它支持音乐教育的智能和个性化的增长，并为未来在该领域的广泛使用AI技术提供理论基础和实用建议。

本文的组织结构如下：在第1条中，引言介绍了音乐教学改革的背景和动机，阐明了研究目标，并阐述了传统音乐教学模型的局限性以及AI技术在音乐教育领域的应用潜力。第2节是文献评论，它回顾了智能音乐教学的当前发展以及DRL在教育领域的应用，并指出了研究差距和创新方面。第3节是研究模型，该模型深入分析了DRL模型在音乐教学中的应用，并提出了基于演员批评框架的音乐教育旋律生成模型。第4节是实验设计和性能评估，详细介绍了实验数据集，实验环境，参数设置以及模型性能的评估结果。最后，第5个是结论，总结了本文的研究贡献，并提示了未来的工作和研究局限性。

音乐教学智能发展的现状

由于信息技术的快速发展，近年来，音乐教育领域已逐渐开始实施智能教学技术。许多学者进行了相关研究。Gao＆Li（2024）⁷在虚拟现实（VR）环境中由移动无线网络支持的单簧管教学进行了探索，并提供了实时反馈以提高学生的游戏技能。冯（2023）⁸设计了一个基于VR技术的音乐教学系统，并通过教育信息实现了个性化的反馈和分级。Faizan等。（2023）⁹在芯片场上可编程的门阵列（SOC-FPGA）设备上实现了一个深度学习模型，以实现实时音乐流派分类并为教学提供了即时分析。张等。（2024）¹⁰提出了一个基于公共云网络深度神经网络的深神网络，以在线音乐教育中有效入侵检测，以保证教学安全。Zheng等。（2023）¹¹使用进化的机器学习来建立一个智能教育大数据平台，以为高等教育提供数据驱动的决策支持。Hosseini等。（2024）¹²提出，进化融合算法和其他领域的最新进展继续提供了一种新的方法来优化该复杂系统中的神经网络。Chen等。（2024）¹³优化基于机器学习的个性化教育建议系统，以实现准确的课程建议。Li等。（2023）¹⁴在大规模开放的在线课程（MOOC）系统中集成了深度学习和大数据，以建立个性化的推荐框架，以满足学习者的各种需求。Xu＆Chen（2023）¹⁵设计了一个个性化的推荐系统，以支持意识形态和政治课程资源的智能建议和实时反馈。Amin等。（2023）¹⁶开发了一个基于强化学习的智能自适应学习框架，以实现个性化的学习路径建议并提高学习效率。

DRL在教育中的应用状态

作为一种将深度学习与强化学习相结合的先进技术，DRL在教育领域的应用近年来逐渐引起了人们的关注。Gu等。（2023）¹⁷使用DRL技术来构建基于元评估的教学建筑疏散培训系统，这使学生能够在虚拟环境中学习紧急响应，并提高他们在实际场景中的决策能力。Sharifani＆Amini（2023）¹⁸展示了DRL的潜力，并研究了在各种领域中使用机器学习和深度学习技术的使用，包括教育中的个性化反馈。泰（2023）¹⁹深入讨论了深度学习和机器学习的架构和应用前景，其中强化学习在教育中的应用为个性化和适应性学习提供了支持。Sanusi等。（2023）20^{系统地回顾了K-12教育中教学机器学习的研究，并指出了DRL在培养学生解决问题的能力方面的重要性。}Han等。（2023）²¹总结了DRL算法在机器人控制中的应用。Gligorea等。（2023）²²在个性化的电子学习路径优化中强调了DRL的应用前景。Mandalapu等。（2023）23^{系统地总结了犯罪预测深度学习的研究，该研究为教育领域的行为预测和风险评估提供了参考。}刘等。（2023）²⁴展示了DRL在复杂的预测任务中的潜在应用，尤其是在教育决策支持中。

在自动学习资源生成方面，DRL的应用也显示出很大的潜力。Lu等。（2023）²⁵提出了一种基于DRL的最佳调度方法，该方法可用于智能调度和优化教育资源的参考。Abouelyazid（2023）²⁶应用对立的DRL技术，确保在生成自动学习资源的过程中的安全性，并确保教育平台和数据安全的稳定性。

研究空白与创新

尽管在音乐教学领域进行了一些基于AI的应用程序探索，但DRL在音乐教育中的应用中仍然存在明显的研究差距。例如，现有的研究重点是单个教学链接，大多数应用程序系统仅限于基本的音乐学习工具，尤其是在复杂的音乐理论，技能培训和创造性实践的整合中。本文创新地将DRL技术应用于多维资源的产生和音乐教育的教学优化，并探讨了如何通过智能算法根据学生实时学习状况动态调整教学策略，以生成个性化的学习材料。最后，它为未来的音乐教育的智能发展提供了理论支持和实践指导。

DRL模型分析

DRL可以通过将强化学习的好处与深度学习相结合，可以根据复杂环境中的实时反馈来适应学习²⁷。特别是在音乐教育中，DRL模型可以通过动态修改教学策略来最大化学生的学习路线²⁸。桌子 1演示了参与者 - 批评（AC）算法和深Q-Network（DQN）总和更好地证明DRL模型在音乐教育中的应用。

在桌上 1，DQN通过深层神经网络构建近似函数。该模型的损耗函数定义为等式。（1）：

李（（â）表示参数下的损失函数â。es，，，，一个，，，，r，，，，s�代表状态的预期价值s， 行动一个， 报酬r和下一个状态s²，也就是说，所有可能的状态过渡都是平均的。y代表目标Q值，由即时奖励组成r以及下一个状态的最大Q值（折扣之后）s²，可以表示为eq。（2）：$$ y = r+\ gamma \ mathop {\ hbox {max}} \ limits _ {{a'}} q \ left（{s'，a';

代表动作时的Q值一个在状态下服用s，并且该Q值由当前参数确定â深度神经网络。r采取行动后立即获得奖励一个在州s。γ代表折现因子，用于衡量未来奖励的当前价值，通常为0€Î³<1。\（q \ left（{s'，a'; \ theta _ {i}^{ - }}}} \ right）\）\）\）代表所有可能动作中的最大Q值一个²下一个状态s²，此Q值由参数确定 -目标网络的1。梯度李（（â） 到â表示为eq。（3）：$$ {\ nabla _ {{\ theta _i}}}} {l_i} \ left（{{{\ theta _i}}} \ right）= {e_ {s，a，a，a，r，r，s'}}}}}} \ left [{r+\ weft（r+\ weft）} \ limits _ {{a'}} q \ left（{s'，a'; \ theta _ {i}^{ - }}}}} \ right） - q \ left（s，a;_i}}}} q \ left（{s，a; {\ theta _i}}} \ right）} \ right] $]（3）

30。^{AC算法的核心优势在于它可以同时优化策略和价值评估，而DQN仅通过Q值指导动作选择。}AC算法属于策略梯度算法，目标函数定义为等式（

4）：$ j \ left（\ theta \ right）\ doteq {\ upsilon _ {{\ pi _ \ theta}}}}}} \ left（{{s_0}} \ right）$$

代表策略梯度算法中假定的策略。\（{s_0} \）代表初始状态。然后是\（j \ left（\ theta \ right）\）\）到我表示为eq。（5）：

\（\ mu \ left（s \ right）\）是策略分布。j（（我）代表目标函数的梯度j（（我）关于策略参数我。\（{q_ \ pi} \ left（{s，a} \ right）\）\）代表采取行动的动作值函数一个在州s，即预期的回报。\（{\ nabla _ \ pi} \ left（{a | s，\ theta} \ right）\）\）代表战略的梯度 -关于参数我也就是采取行动的概率的梯度一个在州s。Actor网络由TD（0）错误更新，如图所示（6）：

它+1表示更新的策略参数。它表示当前的策略参数。±指的是学习率并控制更新步骤大小。\（{g_ {t：t+1}}} \）指的是从时间步长回报t到t+1。\（\ hat {\ varphi} \ left（{{s_t}，w} \ right）\）\）\）指国家的特征表示\（{英石}\）。w是功能的重量。\（{\ delta _t} \）指TD错误。\（{\ nabla _ \ theta} \ pi \ left（{{a_t} | {s_t}，{\ theta _T}}} \ right）\）指战略的梯度 -关于参数我。\（\ pi \ left（{{a_t} | {s_t}，{\ theta _t}}} \ right）\）\）\）指采取行动的可能性在在州英石。\（{\ delta _t} \）表示为eq。（7）：$ $ {\ delta _t} = r+\ gamma q \ left（{{{s_ {t+1}}}，{a_ {t+1}}}}} \ right） - q \ left（{{s_t}，{a_t}}} \ right）$（7）基于AC框架的算法包括确定性策略梯度（DPG）和深层确定性策略梯度（DDPG）算法。基于Q-学习算法的DPG算法中的网络更新。

10）：$$ {\ delta _t} = {r_t}+\ gamma {q^w} \ left（{{s_ {t+1}}，{\ mu _ \ theta}} \ left（{{{{s_t}，{a_t}} \ right）$$（8）

8），\（{r_t} \）表示在时间步骤获得的即时奖励t。γ指折现因子，用于衡量未来奖励的当前价值，通常为0€Î³<1。\ \（{Q^w} \ left（{{s_ {t+1}}，{\ mu _ \ theta} \ left（{{s_ {s_ {t+1}}}}} \ right）} \ right）\ right）指根据策略选择的Q值\（{\ mu _ \ theta} \）在下一个状态\（{S_ {T+1}} \）\）。\（{Q^W} \ left（{{s_t}，{a_t}}} \ right）\）\）\）指采取行动的Q值\（{在}\）在当前状态\（{英石}\）。在等式中（9），wt+1表示更新的评论家网络功能参数。wt指当前Q函数参数。\（{\ alpha _W} \）指Q功能的学习率。\（\ nabla {q^w} \ left（{{s_t}，{a_t}}} \ right）\）\）\）指Q函数的梯度相对于其参数w。在等式中（10），它+1是指更新的策略参数。它指当前参与者网络的策略参数。±指战略的学习率。\（{\ nabla _ \ theta} {\ mu _ \ theta} \ left（{{s_t}}} \ right）\）\）指策略函数有关其参数的梯度我。\（{\ nabla _a} {q^w} \ left（{{s_t}，{a_t}}}} \ right）\）\）\）指Q功能的梯度相对于动作一个。\（{| _ {a = {\ mu _ \ theta} \ left（s \ right）}}} \）代表动作时梯度一个等于策略选择的动作\（{\ mu _ \ theta} \）。DDPG算法中损耗函数的定义在等式中显示（11

）和目标功能的梯度j演员网络关于演员网络参数μ在等式中显示12）：$$ l = \ frac {1} {n} \ sum \ limits_ {i} {{{{{{{y_i} - q \ left（{{s_i}，{a_i}，{a_i}}} \ right）（11）

l是评论家网络的损失函数。n是批处理大小，即用于计算损失函数的样品数量，以及是的是目标Q值。j是Actor网络的目标函数。问是通过关键网络获得的价值函数。\（q'\）是目标关键网络获得的价值函数。\（{\ theta ^q} \）是关键网络参数。\（{\ theta ^{q'}} \）是目标危害网络参数。\（{\ theta ^\ mu} \）是Actor网络参数。\（{\ theta ^{\ mu'}} \）是目标actortor网络参数。\（{\ nabla _ {{\ theta ^\ mu}}}} j \）指目标函数的梯度j有关参数的演员网络的μ演员网络。

因此，本文使用Actor网络生成音符序列或动作序列，而评论家网络评估了这些音符序列的质量，从而优化了学生的学习路径和音乐创作。

基于强化学习的音乐教育中旋律产生模型的构建的分析

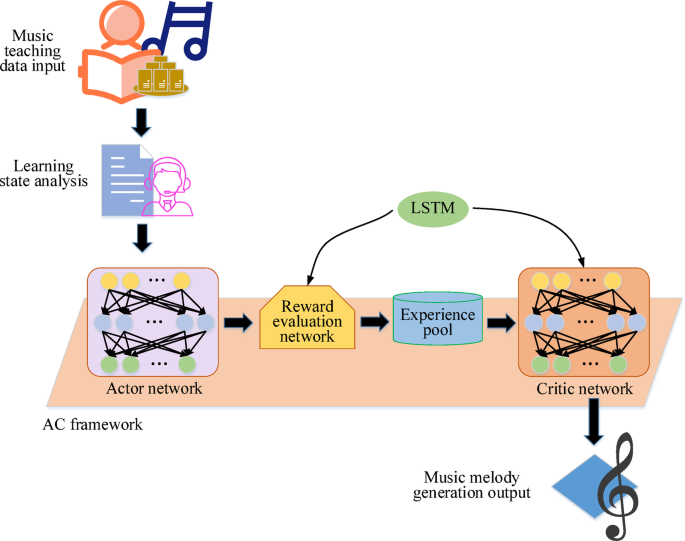
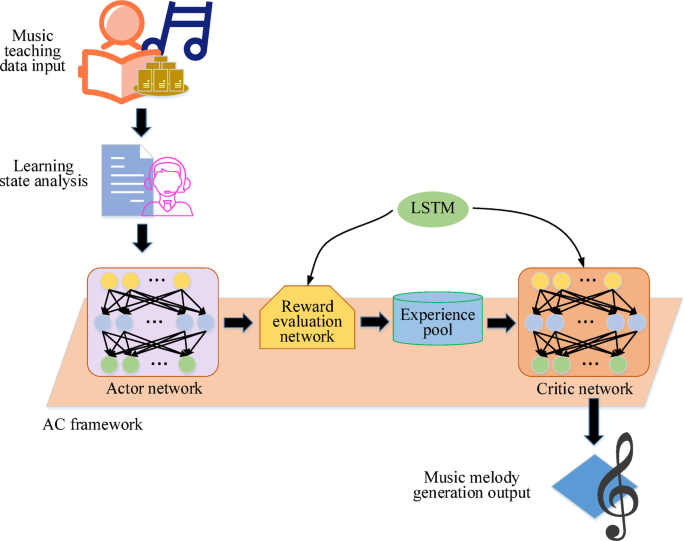
随着教育领域AI技术的逐步渗透，旋律生成是音乐创作的核心任务之一，尤其是如何根据学生的学习进步和音乐风格的需求来产生艺术和技术旋律，这已成为挑战和机遇的研究方向。为了有效地解决这个问题，本文提出了基于强化学习的旋律生成模型，即基于AC框架（AC-MGME）的音乐教育中的旋律生成模型，如图所示。 1。

基于AC框架的音乐教学中旋律生成模型的示意图。

学习状态分析阶段

首先，系统通过学习状态分析模块评估学生当前的学习水平和进步。在此阶段，该系统通过在学习过程中获取学生的数据（例如音高准确性，节奏精通和性能技能）来确定旋律产生的困难和风格。Daneshfar＆Kabudian（2021）³¹提出实时状态分析的概念，不仅包括性能指标，而且还从数据中推断出用户的状态（例如情感）。该原则已在相关领域证明，例如使用高级递归神经网络识别语音情感。具体而言，该系统分析了学生在练习过程中所表现出的技能水平，例如音符的准确性，节奏的稳定性以及不同音乐风格的掌握程度。基于这些数据，系统可以为每个学生自定义个性化的旋律生成任务，以确保生成的旋律不仅与学生当前的学习阶段相匹配，而且还适当地挑战了他们的能力，从而促进了学习的进步。

确定学习状态后，初始注释的生成是演员网络的责任。Actor网络根据当前的学习状态以及上一张注释的上下文信息生成下一个注释或注释序列。这个过程类似于人类音乐家如何根据构图过程中现有的旋律片段和创造意图来决定选择下一张音符的方式。这样，系统可以产生与学生学习进度相符的旋律片段，从而为随后的旋律产生奠定基础。

奖励评估网络阶段

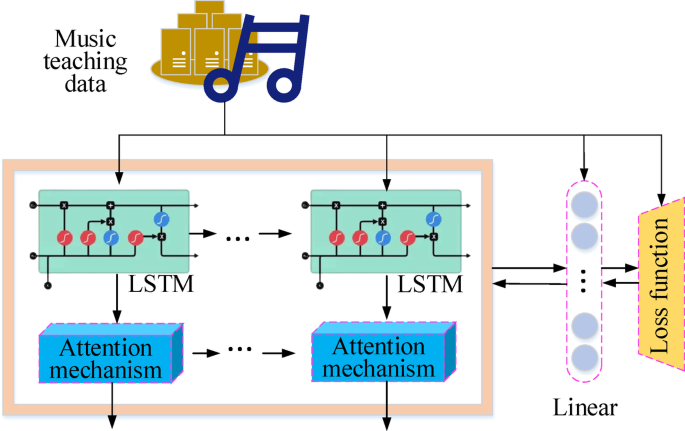
然后通过奖励评估网络评估生成的旋律。该网络的结构如图所示。 2及其核心在于引入注意模块。注意模块的功能是增强学习效果，使网络能够更加关注音符序列中的重要说明。在旋律生成过程中，某些音符（例如高潮注释和旋律的转弯点等）对旋律的整体质量和样式性能产生了至关重要的影响。通过注意机制，该模型可以为这些重要音符分配更高的权重，从而在产生旋律时更加关注这些关键部分的性能。

回报评估网络结构的示意图。

具体而言，注意模块的训练计算过程在等式中显示（13）和等式（14）。其中，等式13）描述线性层输出的组合方法和LSTM（长短期内存）层的输出。通过权重矩阵和偏置向量的操作，注释序列的特征有效地集成了。等式（14）定义损耗函数，并采用Sigmoid跨透明损失函数来测量模型预测与实际标签之间的差异。此损耗功能特别适合多标签分类任务，可以有效地优化模型识别和处理重要说明的能力。

在等式中（13），橄榄是指线性层的输出，该输出通常是神经网络中的中间层。奥尔斯特是指LSTM层的输出，这是用于处理序列数据的特殊复发神经网络。w指重量矩阵，其维度为\（{d_m} * {d_n} \）， 在哪里\（{d_m} \）和\（{d_n} \）分别是输出和输入的维度。\（{w^t} \）指重量矩阵的换位w。b指偏移向量，其维度为\（{d_m} \）， 和\（{d_m} \）是笔记的数量。\（*\）代表矩阵乘法。量损失函数的值量化了实际标签和模型预测之间的差异，被称为等式中的损失。（14）。Sigmoid交叉熵损失函数或Sigmoid_cross_entropy适用于二进制分类任务。Sigmoid Cross熵的另一个符号称为Cross_entropy，它代表交叉渗透损失函数。术语“ sigmoid”是指sigmoid激活函数，该功能经常在二进制分类问题的输出层中使用，并将输入映射到（0，1）间隔。

等式（15）说明如何使用二进制分类模型来计算Sigmoid横熵损耗函数。

x是在激活函数之前模型的输出。p指相应的标签。为了避免Exp（-x）溢出，由太小x什么时候x<<0，等式（15）转换为以下等效形式，例如等式（16）：$$损失= - x \ cdot p+\ log \ left（{1+ \ exp \ left（x \ right）} \ right）$$（16）

）：$$ loss = \ hbox {max} \ left（{x，0} \ right）（17）

p在二进制分类的Sigmoid交叉熵方程中，由于多标签分类中的每个标签确实对应于二进制分类问题。返回值的问题通过返回网络解决，然后在强化学习中的Actor和Ctiric网络基于LSTM网络构建。演员和评论家网络经过四边形数据培训\（\ left（{{{s_t}，{a_t}，{r_ {t+1}}，{s_ {t+1}}}}}} \ right）\）\）

从体验播放池中随机取样，因此首先需要体验收集。首先，初始注释\（{s_ {init}} \）设置为初始状态\（{s_0} \）在模型中，演员网络输出动作\（{a_0} \）根据初始状态\（{s_0} \）和输入\（{a_0} \）进入奖励网络以获得价值回报\（r_ {n}^{1} \）的\（{a_0} \）。此外，为了进一步优化返回值的计算，该模型采用了等式（18）全面考虑音乐的理论回报和实际生产效果的回报。音乐理论返回模块输出音乐理论返回\（r_ {m}^{1} \）对应于\（{a_0} \）根据音乐理论规则，并计算最终回报\（r _ {{mix}}}^{1} \），如等式所示18）：

音乐理论奖励模块将理论奖励值分配给基于音乐理论规则的生成的音符序列，而实际的生成效应奖励是由奖励网络根据旋律的听觉效应和艺术评估的。这样，模型可以平衡音乐理论的正确性和旋律生成期间实际聆听体验的美学吸引力，从而产生高质量的旋律。

下一个状态\（{s_1} \）根据\（{a_0} \）。四边形\（\ left（{{{s_0}，{a_0}，r _ {{mix}}}}^{1}，{s_1}}} \ right）\）\）被放入体验播放池中，依此类推，直到体验中的数据播放到达种子史。

模型训练和旋律生成阶段

在强化学习的参与者批评框架下，参与者网络和评论家网络负责生成音符序列并评估音符序列的质量。两个网络均基于LSTM网络，该网络可以处理序列数据并捕获注释之间的时间序列关系。在训练过程中，系统随机示例四边形数据\（\ left（{{{s_t}，{a_t}，{r_ {t+1}}，{s_ {t+1}}}}}} \ right）\）\）从体验播放池到更新Actor网络和评论家网络的参数。

具体的训练步骤如下：首先，初始音符设置为初始状态\（{英石}\）该模型，演员网络输出动作\（{在}\）根据初始状态，并将其输入奖励网络以获取返回值\（{r_t} \）。同时，音乐理论奖励模块输出音乐理论返回\（r_ {m}^{1} \）对应于\（{在}\）根据音乐理论规则，并计算最终回报值\（r _ {{mix}}}^{1} \）。然后，下一个状态\（{S_ {T+1}} \）\）根据\（{在}\），以及四边形数据\（\ left（{{{s_t}，{a_t}，{r_ {t+1}}，{s_ {t+1}}}}}} \ right）\）\）存储在体验播放池中。当经验中的数据量播放池到达预设的种子步骤时，开始培训演员网络和评论家网络。

培训演员网络时，四核数据\（\ left（{{{s_t}，{a_t}，{r_ {t+1}}，{s_ {t+1}}}}}} \ right）\）\）从经验播放池和状态中随机取样\（{S_ {T+1}} \）\）输入到目标actort网络以获得预测的动作在+1。然后\（{英石}\）和\（{在}\）are input to the Critic network to obtain\(Q\left( {{s_t},{a_t}} \right)\)。然后\({s_{t+1}}\)和在+ 1 are input to the TargetCritic network to obtain\(Q'\left( {{s_{t+1}},{a_{t+1}}} \right)\)。The defined loss function\(J\left( \theta \right)\)of the Actor network trains the Actor, which is expressed by the minimization equation, as shown in Eq. (19）：

The Critic network is trained by the defined loss function\(J\left( w \right)\), and its value evaluation parameters are optimized, as shown in Eq. (20）：

Finally, the melody is generated.According to the probability distribution, the action\({a_0}\)is randomly selected, and\({a_0}\)is turned into the state\({s_1}\)。然后\({s_1}\)is input into the Actor network to obtain the next action, and the note sequence\(S_{n}^{g}\)is generatedltimes in turn.The data processing module combines the note sequence\(S_{n}^{g}\)output by the melody generation model and the rhythm sequence\(S_{n}^{g}\)generated by the rhythm generation model into a complete MIDI (Musical Instrument Digital Interface) format music file as the final result.

This strategy updating process ensures that the generated melody can be optimized artistically and technically.Through continuous learning and optimization, the model can adaptively improve the quality of melody generation, while maintaining the diversity and creativity of generated content.Thus, the pseudo-code flow of this model is shown in Fig. 3。

Pseudo code flow chart based on AC-MGME model algorithm.

Datasets collection

To comprehensively verify the effectiveness and universality of the proposed algorithm, this study adopts two large-scale public MIDI datasets.First, the LAKH MIDI v0.1 dataset (https://colinraffel.com/projects/lmd/) is used as the main training data.It is a large-scale dataset containing over 170,000 MIDI files, and its rich melody, harmony, and rhythm materials provide a solid foundation for the model to learn music rules.In the data preprocessing stage, this study filters out piano music MIDI files from the LMD dataset because their melodic structures are clear, making them suitable as basic training materials for melody generation models.

However, to address the limitation of the LAKH MIDI dataset being dominated by piano music and test the model’s universality across a wider range of instruments, this study introduces a second multi-instrument dataset for supplementary verification.It adopts the MuseScore dataset (https://opendatalab.com/OpenDataLab/MuseScore), which is a large-scale, high-quality dataset collected from the online sheet music community MuseScore.The core advantage of this dataset lies in its great instrumental diversity, covering sheet music from classical orchestral music to modern band instruments (such as guitar, bass, drums) and various solo instruments.This provides an ideal platform for testing the model’s ability to generate non-piano melodies.

For both datasets, a unified preprocessing workflow is implemented:

1) Instrument Track Filtering: For the LAKH MIDI dataset, this study uses its metadata to filter out MIDI files with piano as the primary instrument.For the MuseScore dataset, which contains complex ensemble arrangements, it applies heuristic rules to extract melodic tracks: prioritizing tracks in MIDI files where the instrument ID belongs to melodic instruments (such as violin, flute, saxophone, etc.) and which have the largest number of notes and the widest range.

2) Note Information Extraction: This study uses Python’s mido library to parse each MIDI file.From the filtered tracks, it extracts four core attributes of each note: Pitch (i.e., MIDI note number, 0-127);Velocity (0-127);Start Time (in ticks);and Duration (in ticks).

3) Time Quantization and Serialization: To standardize rhythm information, it quantizes the start time and duration of notes to a 16th-note precision.This means discretizing the continuous time axis into a grid with 16th notes as the smallest unit, where all note events are aligned to the nearest grid point.All note events are strictly sorted by their quantized start time to form a time sequence.

4) Feature Engineering and Normalization: To eliminate mode differences, each melody is transposed to C major or a minor, allowing the model to focus on learning relative interval relationships rather than absolute pitches.Finally, each note event is encoded into a numerical vector.A typical vector might include: [normalized pitch, quantized duration, interval time from the previous note].The sequence formed by these vectors serves as the final input to the model.

5) Data Splitting: All preprocessed sequence data are strictly divided into training and test sets in an 80%/20% ratio.

Experimental environment and parameters setting

To ensure the efficiency of the experiment and the reliability of the results, this paper has carefully designed the experimental environment and parameter settings.The experiment uses a high-performance computing cluster equipped with NVIDIA Tesla V100 GPUs to accelerate the model training process.This GPU has strong parallel computing capabilities and can effectively handle the computational burden brought by large-scale datasets.The model training is implemented based on the TensorFlow 2.0 framework, and Keras is used to construct and optimize the neural network structure.Due to the large scale of the LMD dataset, the training process requires a large amount of time and computational resources.Therefore, multi-GPU parallel computing technology is adopted in the experiment.Through multi-GPU parallel computing, the training time can be significantly shortened, and the experimental efficiency can be improved.In addition, the hyperparameters of the model have been carefully adjusted and optimized in the experiment to ensure that the model can achieve the best performance during the training process.桌子 2displays the parameter settings.Table 2 Experimental parameter setting.

The tuning method involved dividing 10% of the training set into a Validation Set, with the selection of all hyperparameters ultimately judged by the model’s F1 score on this validation set.

Search space and selection reasons for key hyperparameters:

1) Learning Rate: Searched within the range of [1e-3, 1e-4, 5e-5].Experiments showed that a learning rate of 1e-3 led to unstable training with severe oscillations in the loss function, while 5e-5 resulted in excessively slow convergence.The final choice of 1e-4 achieved the best balance between convergence speed and stability.

2) Batch Size: Tested three options: [32, 64, 128].A batch size of 128, though the fastest in training, showed slightly decreased performance on the validation set, possibly getting stuck in a poor local optimum.A batch size of 64 achieved the optimal balance between computational efficiency and model performance.

3) Number of LSTM Layers: Tested 1-layer and 2-layer LSTM networks.Results indicated that increasing to 2 layers did not bring significant performance improvement but instead increased computational costs and the risk of overfitting.

4) Number of Neurons: Tested hidden layer neuron counts in [128, 256, 512].256 neurons proved sufficient to capture complex dependencies in melodic sequences, while 512 neurons showed slight signs of overfitting.

5) Reward Function Weights: Tested weight ratios of artistic/technical aspects in [0.5/0.5, 0.7/0.3, 0.9/0.1].Through subjective listening evaluation of generated samples, the ratio of 0.7/0.3 was deemed to best balance the melodic pleasantness and technical rationality.

Performance evaluation

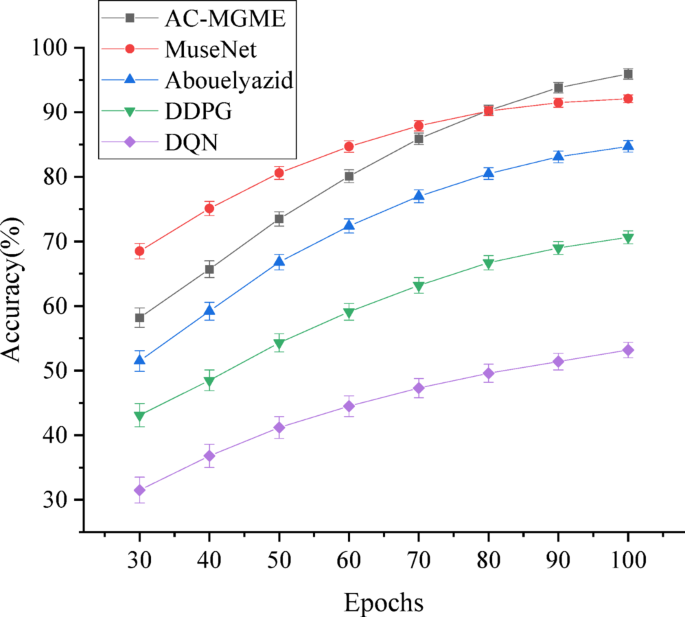
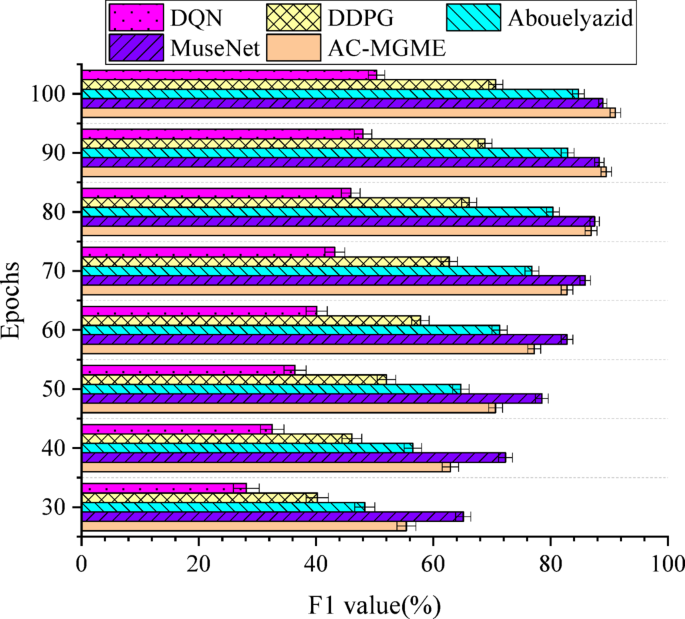
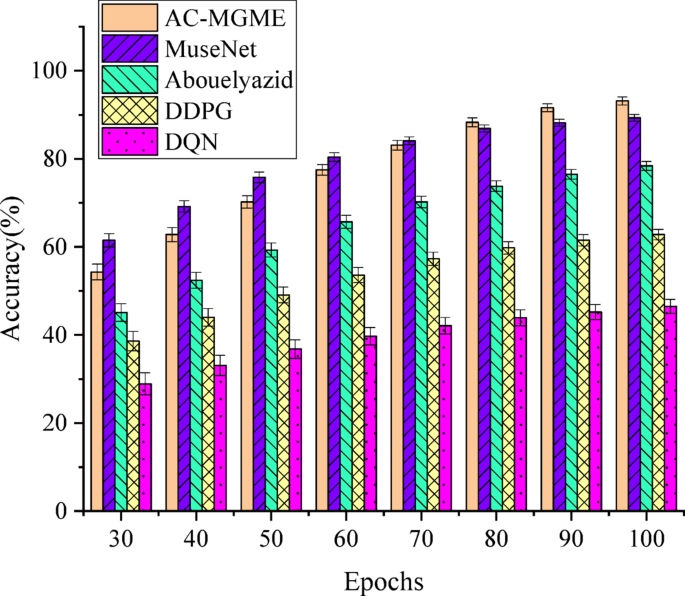
To evaluate the performance of the constructed model, the proposed AC-MGME model algorithm is compared with the model algorithm proposed by DQN, MuseNet³², DDPG³³and Abouelyazid (2023), and the Accuracy, F1-score, and melody generation time are evaluated.The results in LAKH MIDI v0.1 dataset are shown in Figs. 4，，，，5和6。

Accuracy results for music melody prediction by various algorithms in the LAKH MIDI v0.1 dataset.

F1-score results for music melody prediction by various algorithms in the LAKH MIDI v0.1 dataset.

In Figs. 4和5, it can be found that on the LAKH MIDI dataset, the proposed AC-MGME model algorithm achieves the highest scores in both key indicators: accuracy (95.95%) and F1 score (91.02%).From the perspective of the learning process, although the Transformer-based State-of-the-Art (SOTA) model MuseNet shows strong competitiveness in the early stage of training, the AC-MGME model, relying on its efficient reinforcement learning framework, demonstrated greater optimization potential and successfully surpassed MuseNet in the later stage of training.This not only proves the superiority of its final results but also reflects its excellent learning efficiency.At the same time, AC-MGME maintained a leading position in all stages compared with other reinforcement learning-based comparison models (such as DDPG, DQN, etc.).

To more rigorously verify whether the leading advantage of the AC-MGME model in accuracy is statistically significant, a two-sample t-test is conducted on the results of each model in the final training epoch (Epoch 100).The significance level (α) adopted is 0.05, that is, when the p-value is less than 0.05, the performance difference between the two models is considered statistically significant, as shown in Table 3。

In Table 3, the test results clearly demonstrate that the performance advantage of the AC-MGME model over all comparison models in terms of the key accuracy indicator is statistically significant.Specifically, even when compared with the powerful benchmark model MuseNet, its p-value (0.021) is far below the 0.05 significance threshold, and the differences from models such as DDPG and DQN are even more pronounced (p < 0.001).This conclusion is further confirmed by the F1 score, which more comprehensively reflects the model’s precision and recall.AC-MGME is also significantly superior to all comparison models in terms of F1 score (all p-values are less than 0.05).Overall, these statistical test results fundamentally rule out the possibility that the observed performance differences are caused by random factors.It provides solid and quantitative statistical evidence for the core assertion that the proposed AC-MGME model exhibits strong performance in both generation accuracy and comprehensive performance.

The comparison result chart of music melody generation time by each algorithm in LAKH MIDI v0.1 dataset.

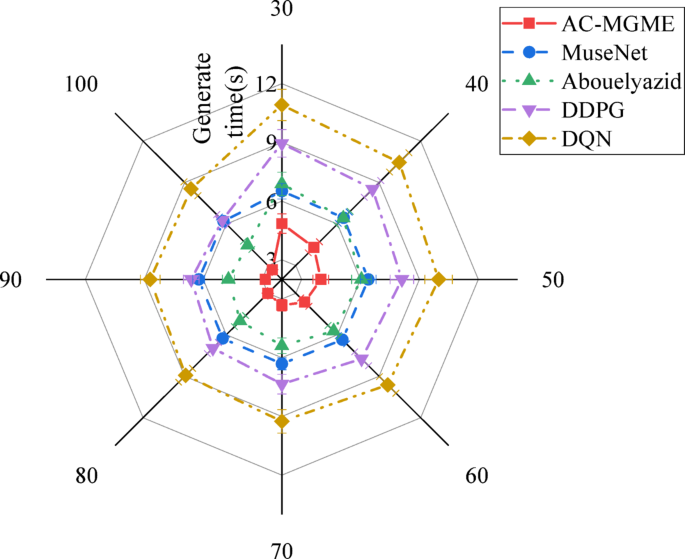
数字6illustrates how the developed AC-MGME model outperforms previous contrast models in terms of melody creation time efficiency.From the figure, the generation time of AC-MGME decreases steadily with the progress of training, reaching the lowest value among all models at the 100th epoch, which is only 2.69 s.In sharp contrast, the Transformer-based SOTA model MuseNet maintains an inference time of over 6.2 s, highlighting the limitations of large-scale models in real-time applications.Meanwhile, the efficiency of AC-MGME is also significantly superior to all other reinforcement learning-based comparison models.

To further verify the superiority of the AC-MGME model in computational efficiency from a statistical perspective, a two-sample t-test is similarly conducted on the melody generation time of each model at the final epoch (Epoch 100), as shown in Table 4。

In Table 4, in comparisons with all contrast models (including the heavyweight MuseNet and other reinforcement learning models), the p-values are all far less than 0.001.This extremely low p-value indicates that the shorter generation time exhibited by the AC-MGME model is not a random fluctuation in the experiment, but a significant advantage with high statistical significance.This finding provides decisive statistical evidence for the applicability of the model in real-time personalized music teaching applications that require rapid feedback.

To verify the generalization ability of the AC-MGME model in more complex musical environments, the final accuracy rates on the MuseScore dataset are compared, as shown in Fig. 7。

Accuracy results for music melody prediction by various algorithms in the MuseScore dataset.

In Fig. 7, due to the significantly greater complexity and diversity of the MuseScore dataset in terms of instrument types and musical styles compared to the LAKH dataset, there is a universal decline in the accuracy of all models, which precisely reflects the challenging nature of this testing task.Nevertheless, the AC-MGME model once again demonstrats its strong learning ability and robustness, topping the list with an accuracy rate of 90.15% in the final epoch.It is particularly noteworthy that, in the face of complex musical data, the advantages of AC-MGME over other reinforcement learning models (such as DDPG and DQN) are further amplified.It successfully surpasses the powerful SOTA model MuseNet in the later stages of training.This result strongly proves that the design of the AC-MGME model is not overfitted to a single type of piano music, but possesses the core ability to migrate and generalize to a wider and more diverse multi-instrument environment, laying a solid foundation for its application in real and variable music education scenarios.

To verify whether the generalization ability of the AC-MGME model across a wider range of instruments is statistically significant, a two-sample t-test is similarly conducted on the accuracy results of each model at the final epoch (Epoch 100) on the MuseScore dataset, as shown in Table 5。

In Table 5, the test results indicate that the performance advantage of the AC-MGME model is statistically significant.Even in comparison with its strongest competitor, MuseNet, its p-value (0.042) is below the 0.05 significance level.While the differences from models such as Abouelyazid (2023), DDPG, and DQN are even more pronounced (p < 0.001).This strongly proves that the leading position of this model on diverse, multi-instrument datasets is not accidental.More importantly, this conclusion fundamentally confirms the robustness and generality of the AC-MGME framework, indicating that it is not limited to the generation of single piano melodies but can effectively learn and adapt to the melodic characteristics of a wider range of instruments, thus having application potential in more diverse music education scenarios.

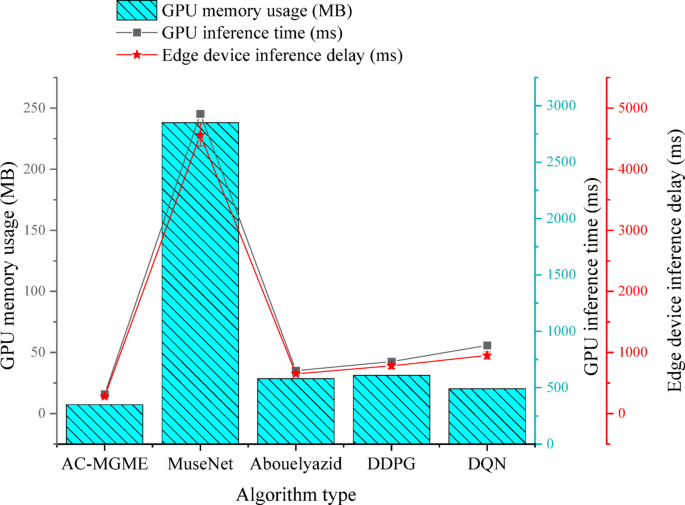
To evaluate the deployment potential of the model in real teaching scenarios, a dedicated test on inference performance and hardware resource consumption is conducted.The model’s performance is assessed not only on high-performance servers but also deploys on a typical low-power edge computing device (NVIDIA Jetson Nano) to simulate its operation on classroom tablets or dedicated teaching hardware.The comparison of inference performance and resource consumption of each model on high-performance GPUs and edge devices is shown in Fig. 8。

Comparison table of reasoning performance and resource occupation of each model on high-performance GPU and edge devices.

In Fig. 8, an analysis of the inference performance and resource consumption test reveals the significant advantages of the proposed AC-MGME model in practical deployment.In the high-performance GPU (NVIDIA Tesla V100) environment, AC-MGME not only demonstrated the fastest inference speed (15.8 milliseconds) but also had a GPU memory footprint (350 MB) far lower than all comparison models.Particularly when compared with the heavyweight Transformer model MuseNet (2850 MB), it highlighted the advantages of its lightweight architecture.More crucially, in the test on the low-power edge device (NVIDIA Jetson Nano) simulating real teaching scenarios, the average inference latency of AC-MGME was only 280.5 milliseconds, fully meeting the requirements of real-time interactive applications.

Two objective indicators, namely Pitch Distribution Entropy and Rhythmic Pattern Diversity, are further introduced to quantify the musical diversity and novelty of the generated melodies.This helps evaluate whether the model can generate non-monotonous and creative musical content.Among them, Pitch Distribution Entropy measures the richness of pitch usage in a melody.A higher entropy value indicates that the pitches used in the melody are more uneven and unpredictable, usually implying higher novelty.Rhythmic Pattern Diversity calculates the unique number of different rhythmic patterns (in the form of n-grams) in the melody.A higher value indicates richer variations in the rhythm of the melody.The comparison results and statistical analysis of the objective musicality indicators of the melodies generated by each model are shown in Table 6。

桌子 6reveals the in-depth characteristics of each model in terms of musical creativity, and its results provide more inspiring insights beyond the single accuracy indicator.As expected, MuseNet, as a large-scale generative model, obtains the highest scores in both Pitch Distribution Entropy and Rhythmic Pattern Diversity, and statistical tests shows that its leading advantage is significant (p < 0.05), which proves its strong ability in content generation and innovation.However, a more crucial finding is that the AC-MGME model proposed in this study not only demonstrates highly competitive diversity but also significantly outperforms all other reinforcement learning-based comparison models in both indicators (p < 0.01).This series of results accurately indicates that the AC-MGME model proposed in this paper does not pursue unconstrained and maximized novelty, but rather achieves much higher musical diversity and creativity than similar DRL models on the premise of ensuring the rationality of musical structures.This good balance between “controllability” and “creativity” is an important reason why it obtained high scores in subsequent subjective evaluations, especially in “teaching applicability”.

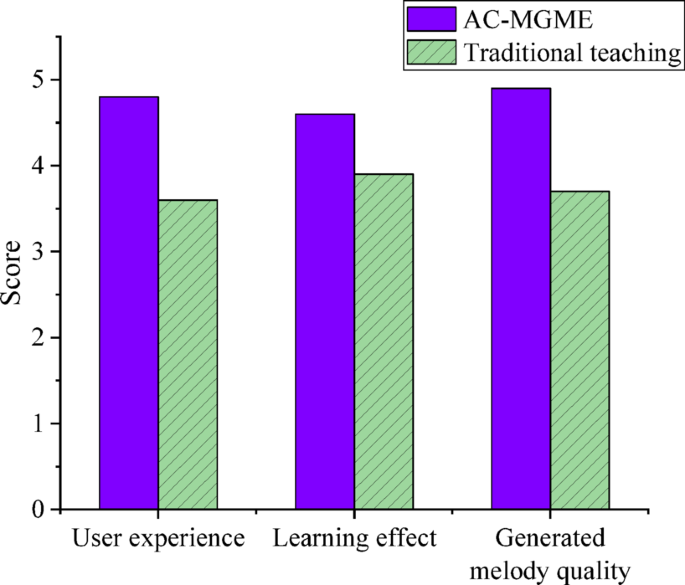
To evaluate the subjective artistic quality and educational value that cannot be captured by technical indicators, a double-blind perception study is conducted.30 music major students and 10 senior music teachers with more than 5 years of teaching experience are invited as expert reviewers.The reviewers score the melody segments generated by each model anonymously on a 1–5 scale (higher scores indicate better performance) without knowing the source of the melodies.The user feedback results under the proposed model algorithm are further analyzed, including the scores (1–5 points) in three aspects: the use experience, the learning effect and the quality of the generated melody.The comparison results with traditional music teaching and learning are shown in Fig. 9。

Comparison chart of user feedback results.

In Fig. 9, according to the feedback from users, the satisfaction of AC-MGME model is higher than that of traditional music teaching.Especially in the aspect of melody quality, AC-MGME gets a high evaluation of 4.9 points, which is significantly better than the traditional teaching of 3.7 points.In addition, AC-MGME also performs well in terms of experience and learning effect, with scores of 4.8 and 4.6 respectively, far exceeding the scores of 3.6 and 3.9 in traditional teaching.This shows that AC-MGME model not only improves the learning effect and student experience, but also provides higher quality results in melody creation.

The expert evaluation results of subjective quality of melodies generated by each model are shown in Table 7, and the statistical analysis results are shown in Table 8。

The results of Tables 7和8show that, in the dimension of artistic innovation, MuseNet achieves the highest score with its strong generative capability, and its leading advantage is statistically significant (p = 0.008), which is completely consistent with the conclusion of the objective musicality indicators.However, in terms of melodic fluency, AC-MGME won with a slight but statistically significant advantage (p = 0.041), and expert comments generally considered its melodies to be “more in line with musical grammar and more natural to the ear”.The most crucial finding comes from the core dimension of teaching applicability, where the AC-MGME model obtained an overwhelming highest score (4.80), and its advantage over all models including MuseNet is highly statistically significant (p < 0.001).The participating teachers pointed out that the melodies generated by AC-MGME are not only pleasant to listen to, but more importantly, “contain clear phrase structures and targeted technical difficulties, making them very suitable as practice pieces or teaching examples for students”.This series of findings strongly proves that while pursuing technical excellence, this model more accurately meets the actual needs of music education, and can generate educational resources that combine artistic quality and practical value.This is a unique advantage that cannot be matched by models that simply pursue novelty or accuracy.

讨论

The results of this study clearly demonstrate the comprehensive advantages of the AC-MGME model across multiple dimensions.In terms of objective performance, the model not only outperforms all comparison benchmarks, including state-of-the-art models, in accuracy and F1 score, but also confirms the reliability of this advantage through strict statistical significance tests (p < 0.05).More importantly, in the subjective quality evaluation, AC-MGME achieved an overwhelming highest score in “teaching applicability”, indicating that it does not simply pursue technical indicators, but precisely meets the core needs of music education—generating musical content that combines structural rationality, artistic fluency, and teaching practical value.In addition, through deployment tests on low-power edge devices, this study is the first to empirically prove that while ensuring high-quality generation, the model has great potential for efficient and low-latency deployment in real classroom environments, laying a solid foundation for its transition from theory to application.

This study indicates that the proposed AC-MGME model exhibits significant performance in terms of melody generation quality, learning effectiveness, and user experience.In terms of melody generation quality, the AC-MGME model scores 4.9/5, which is higher than that of traditional music teaching, demonstrating its strong ability to generate melodies with both artistic and technical merits.Meanwhile, AC-MGME also performs well in learning effectiveness, with a score of 4.6/5, which is higher than traditional teaching, proving its effectiveness in generating personalized learning paths and improving students’ skills.In terms of user experience, AC-MGME scores 4.8/5, also higher than traditional teaching (3.6/5), further verifying the advantages of the interactive and convenient teaching system based on DRL.This is consistent with the findings of Dadman et al.(2024)³⁴and Udekwe et al.(2024)³⁵。Particularly in terms of generation time, AC-MGME only takes 2.69 s to generate a melody, while other models such as DQN require 8.54 s.AC-MGME not only improves the generation quality but also significantly enhances the generation efficiency.In addition, the model performs excellently in terms of generation quality (with an accuracy rate of 95.95% and an F1 score of 91.02% on the LAKH MIDI dataset), and its generation quality is higher than that of other tested models, supporting the feasibility of real-time applications.This is consistent with the research of Chen et al.(2024)³⁶。

Therefore, the proposed model algorithm can efficiently generate melody and provide personalized learning experience.By dynamically adjusting the melody generation strategy, AC-MGME can optimize the generated content in real time according to students’ different needs and learning progress, which greatly improves the intelligence and personalization level of music education and provides valuable practical basis for the development of AI-driven music education tools in the future.

However, while affirming these achievements, people must carefully recognize the limitations and potential biases in the research.Firstly, in terms of datasets, although the introduction of the MuseScore dataset has greatly expanded the diversity of instruments, the content of both datasets still mainly focuses on Western tonal music.This may lead to poor performance of the model when generating non-Western music or modern atonal music, resulting in an “over-representation” bias in a broader cultural context.Secondly, the size of the user sample is also a limiting factor.Although the expert review panel composed of 40 music professionals has provided valuable in-depth insights, this scale is not sufficient to fully represent the diverse perspectives of global music educators and learners.Therefore, although the results of this study are robust within the test framework, caution is still needed when generalizing them to all music cultures and educational systems, and more localized verifications should be conducted.

Finally, the application of such AI technologies in the field of education will inevitably raise ethical issues that require serious attention.A core concern is the potential risk of abuse, particularly music plagiarism.The model may learn and reproduce copyrighted melody segments during training, thereby triggering intellectual property issues.To mitigate this risk, future system iterations must integrate plagiarism detection algorithms, for example, by comparing generated content with n-gram sequences in the training set, and design corresponding reward mechanisms to encourage originality.Another equally important ethical issue is the privacy and security of student data.While tracking and analyzing students’ practice data can enable personalized teaching, it also involves sensitive personal performance information.To address this, strict data management strategies must be adopted, including anonymizing and aggregating all data, ensuring system design complies with relevant regulations such as the General Data Protection Regulation (GDPR), and fully disclosing the content, purpose, and usage of data collection to students, parents, and teachers.These measures aim to build a trustworthy and responsible intelligent music education ecosystem.

Research contribution

This paper innovatively proposes a DRL model (AC-MGME) based on the AC framework for intelligently generating melody resources in music education, and demonstrates its significant advantages in melody generation quality, learning outcomes, and user experience through experiments.Specifically, the AC-MGME model can generate high-quality melodies in real-time according to students’ learning progress and needs, enhancing the personalization and intelligence of music teaching.Experimental results show that AC-MGME outperforms traditional teaching methods and other DRL models in terms of melody generation quality, learning outcomes, and generation efficiency.It achieves an accuracy of 95.95% and an F1 score of 91.02%, while the time taken to generate melodies is only 2.69 s, significantly improving generation efficiency.This provides a new theoretical framework and practical basis for the development of personalized education and intelligent teaching tools.

Future works and research limitations

Although the proposed AC-MGME model has achieved remarkable results in melody generation in music teaching, there is still room for improvement.Future research can further explore the generation performance in diverse music styles and complex structures, for example, combining the Generative Adversarial Network or Variational Autoencoder to enhance melody diversity and creativity.In addition, to verify the wide applicability of the model, more types of datasets can be introduced in the future to test the adaptability of different music styles.At the same time, more accurate personalized demand modeling and multimodal data combination are also potential improvement directions to enhance the personalized adaptability and teaching support function of the model.

Authors and Affiliations

1. School of Music and Dance, Qiqihar University, Qiqihar, 161000, China

   Ding Cheng & Xiaoyu Qu

贡献

Ding Cheng: Conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation, Xiaoyu Qu: writing—review and editing, visualization, supervision, project administration, funding acquisition.

相应的作者

对应Xiaoyu Qu。

竞争利益

作者没有宣称没有竞争利益。

道德声明

The studies involving human participants were reviewed and approved by School of Music and Dance, Qiqihaer University Ethics Committee (Approval Number: 2022.6252561002).参与者提供了书面知情同意，以参加这项研究。All methods were performed in accordance with relevant guidelines and regulations.

Publisher’s note

关于已发表的地图和机构隶属关系中的管辖权主张，Springer自然仍然是中立的。

开放访问This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material.您没有根据本许可证的许可来共享本文或部分内容的改编材料。The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.To view a copy of this licence, visithttp://creativecommons.org/licenses/by-nc-nd/4.0/。重印和权限

关于这篇文章