OC
英语轻松读发新版了，欢迎下载、更新

使用机器学习间电位预测镍 - 山基随机合金中的氢扩散

2025-08-23 13:01:01 英文原文

作者：Matsunaga, Hisao

介绍

为了达到碳中立性并解决能源资源耗竭，氢经济正在以加速速度发展1，，，，2，随着全球各种计划的发展3，，，，4，，，，5，，，，6，，，，7，，，，8，，，，9，，，，10，，，，11。氢社会包括从氢生产，运输，存储和供应到利用的所有阶段，并具有显着的进步，特别是用于氢利用率4。氢燃料电池汽车（FCV）是使用氢作为燃料并发射二氧化碳的碳5，，，，12。随着FCV的扩散，加油站的发展也正在发展13。但是，在这样的系统中，特定的金属组件（例如管道和阀门）暴露于高压氢环境中。此外，氢可以穿透这些材料，可能降低其强度和延展性14，，，，15，，，，16，，，，17。这种现象通常被称为氢含水（HE）18，，，，19，，，，20，，，，21，，，，22。

具有高奥氏体稳定性的奥斯丁质不锈钢（ASS）主要用于FCV和氢气站23，，，，24。为了扩大可用材料的范围，最近的研究调查了他在不同奥氏体稳定性的屁股中的行为。在这些研究中，使用通过高压氢气引入的外部氢或通过暴露于高压氢气的外部氢来评估HE行为25，，，，26。氢环境中的延展性随着奥氏体稳定性而降低27，，，，28，，，，29，，，，30，，，，31，，，，32。尽管正在对奥氏体合金进行广泛的研究33，，，，34，，，，35，，，，36，，，，37，，，，38，，，，39，基本机制尚未完全理解，因为它们随材料，环境条件和加载状态而变化。特别是对于高压氢环境，即使在室温下，原子氢很容易溶于金属，从而导致HE。因此，必须理解金属中的氢溶解度和运输（扩散），以制定针对这种环境中使用的材料的设计指南。

几项研究研究了在高压氢气下实用不锈钢中的氢溶解度和扩散系数40，，，，41。但是，实用合金包含各种合金元件，旨在增强其耐腐蚀性，耐药性和相位稳定性。为了消除其他冶金因素引入的复杂性，Omura等人。42研究了某些合金元素（FE，CR，MN，MO）对使用简单的二元NI的高压氢在高压氢下Ni氢溶解度和扩散系数的影响x奥氏体合金。此外，ITO等人。43半定量性使用密度功能理论（DFT）计算的氢溶解度的实验结果，并阐明了合金元素的作用机理。然而，氢扩散系数上合金元件的作用机理，这是另一个重要因素，尚未通过计算复制，也没有根据计算结果来解释。对于纯Ni，使用基于DFT的声子计算与过渡状态理论的氢扩散系数的非经验计算已定量再现了实验结果44。但是，基于DFT的合金系统中氢扩散系数的计算在计算上不是实际的，因为必须全面评估由随机原子位置引起的各种扩散路径。最近据报道，使用基于DFT的机器学习模型和动力学蒙特卡洛（KMC）模拟的组合计算氢扩散系数45，，，，46。但是，对于这些KMC方法，必须提供扩散尝试频率作为参数，因此预测是半经验的，而不是完全非经验的45，，，，46。此外，由于尚未将结果与实验数据进行比较，因此预测有效性尚不清楚。相比之下，使用经验的Nih构建经验的原子间电位的分子动力学（MD）计算，它们是在强调与DFT一致性的同时构建的，可以重现氢扩散系数的实验结果47。然而，建造高度准确的经验跨性别潜力x-h三元系统表现出磁性，很难48。最近，已经为许多系统开发了机器学习的原子间电位（MLIP）49，，，，50，，，，51，，，，52，包括ni53，，，，54，，，，55，FE及其二进制系统56，，，，57，，，，58，，，，59，，，，60，，，，61，，，，62，，，，63，，，，64，，，，65，，，，66，，，，67，，，，68，表现出磁性。MLIP也已应用于分析含氢的二元系统中的氢扩散69，，，，70，，，，71，，，，72。但是，MLIP降低了外推区域的精度73而且，据我们所知，在多种原子环境下，尚无可以在随机合金中重现氢扩散行为的三元MLIP。在这项研究中，Niâmlipx开发了H系统，并使用此潜力进行MD模拟，以非经验预测随机合金中的氢扩散系数。通过与实验结果进行比较来验证预测。此外，对模拟结果的详细分析阐明了合金元素对原子水平氢扩散的影响。特别是，采用了一种主动学习方法，用于MLIP结构，其中通常基于原子力的基于不确定性的方法74与基于结构的筛选过程结合75。该方法允许对合金中与氢扩散相关的多种原子环境进行有效抽样，从而促进了高精度MLIP的构建。但是，MLIP的开发和后续分析产生了实质性的计算成本。因此，本研究的重点是NiâMn合金系统。尽管该系统的实验研究表明氢扩散系数对MN浓度的非线性依赖性42，基本机制尚不清楚。因此，该系统提出了一个合适的案例，用于证明基于MLIP的分析的实用性。值得注意的是，这项研究中采用的方法不仅限于NiâMN系统，而且适用于其他随机合金系统。因此，这项研究提出了一种对随机合金中氢扩散行为的非经验预测的方法，并为氢转运提供了深层原子水平的见解。这些发现将扩展计算材料科学在氢环境设计材料设计中的作用，并支持碳中性社会的实现。

结果与讨论

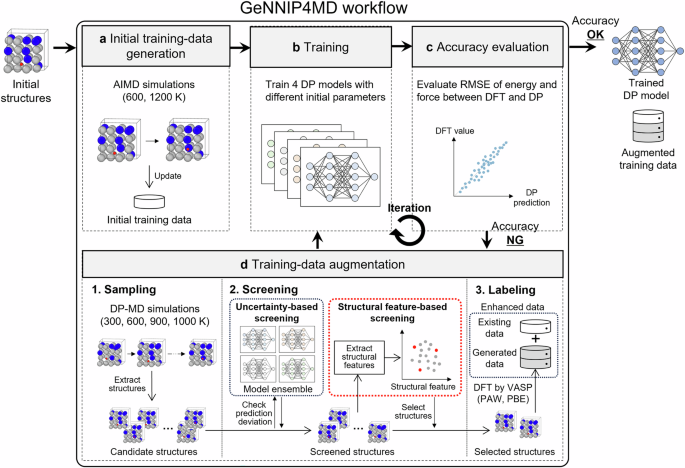
使用GenNIP4MD的MLIP结构概述

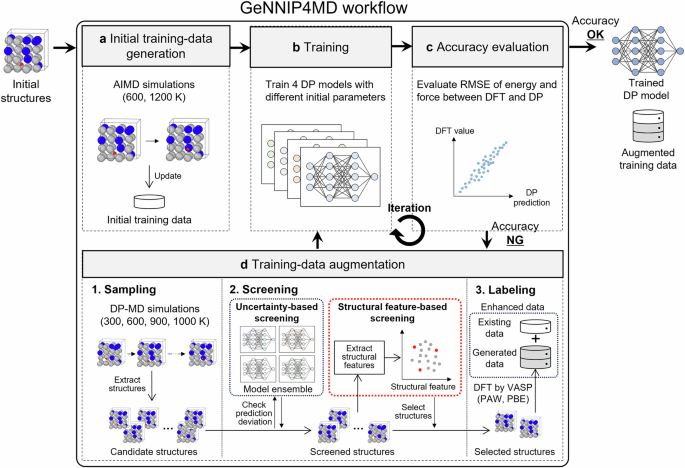
在本小节中，概述了Ni -Mn H Mlip的施工程序。在结果和讨论部分的后续小节中，我们通过与DFT计算进行比较，证明了发达的MLIP在复制与氢扩散和其中的氢相关的NiâMn合金和氢行为的准确性。此外，我们报告了根据使用设计的MLIPS进行的MD模拟确定的Ni-MN合金中的氢 - 扩散系数，并将这些系数与实验值进行比较。基于这些计算结果，我们在原子量表上揭示了Mn对原子量表下氢扩散的影响。最后，我们讨论了本研究中进一步发展方法和见解的潜力。方法部分描述了通过MD模拟来计算氢扩散系数的方法，该方法在方法部分中描述了应采样以构建MLIP训练数据集的原子环境。训练数据库生成和MLIP培训过程也在方法部分中进行了描述，并提供了用于训练DATA生成和验证的DFT设置的详细信息。在这项研究中，我们为Ni -Mnh系统构建了一个MLIP，可以准确预测氢扩散系数。这是使用最近开发的gennip4md软件包实现的75，这是一种MLIP构造工具。基于原子能不确定性的主动学习方法，该方法在DP-gen软件平台中提供74，广泛用于MLIP结构。在GenNIP4MD中，采用了更复杂的主动学习方法75，结合了基于不确定性的主动学习74基于结构特征的额外筛选过程。GenNIP4MD可能可以有效地生成最紧凑，最适当的培训数据集，以进行高智度MLIP75。在这项研究中，我们采用了DP框架76，这是在DP-Gen中使用的。GenNIP4MD的当前实施支持DP框架，包括M3GNET77和Chgnet78。但是，原则上，它也可以扩展到其他潜在形式，例如BellerâParrinello神经网络电位（BNNP）79，原子簇扩展（ACE）80，力矩张量电势（MTP）81，高斯近似电势（GAP）82，和光谱邻居分析势（SNAP）83。使用GenNIP4MD的MLIP构建方法如图所示。 1。在准备初始培训数据集后，迭代执行模型培训和训练数据生成过程，直到模型达到足够的预测准确性为止。训练数据生成过程包括三个步骤：（1）候选结构的生成（抽样），（2）通过主动学习筛选候选结构，以及（3）DFT标记筛选的结构以创建标记的培训数据集。首先，使用初始训练数据对具有不同初始参数的多个DP模型进行了训练（图 1B）。在随后的步骤中，产生了候选结构（图 1d），其中一种DP模型（例如，四个）用于对目标原子系统进行多个MD模拟。例如，在各种温度和压力条件下进行长期退火。因此，产生了大量多样的候选原子结构。在下一步中，采用两种筛选方法来选择训练数据候选者。首先，进行了基于不确定性的筛选，通过评估了多个DP模型预测的原子力中的偏差。选择了预定义的下阈值和上阈值内的结构。这些阈值设置为可以适当识别模型未训练的结构，并且预测误差很高。在DP-GEN中，通过这种基于不确定性的筛选选择的结构直接用于标记。相比之下，GenNIP4MD工具进一步应用了基于结构特征的筛选，以基于不确定性方法选择的结构。详细评估了不确定性选择的结构与现有培训数据之间的相似性，并且优先选择了相似性低的结构。与使用DP-gen相比，使用GenNIP4MD的迭代周期更少的迭代周期和较小的训练数据集预计，这种双重筛选过程有望产生高临界的MLIP结构。75，，，，84。在随后的步骤中，即标记，DFT计算是对两种筛选方法选择的结构进行的，以生成标记的训练数据。然后使用新获得的培训数据集对DPS进行重新训练。评估了再培训DPS的预测精度，并在必要时重复数据生成和模型再培训过程。经过充分的迭代，通过使用初始添加和新添加的培训数据集的培训获得了最终的DP。

图1：使用GenNIP4MD进行深度电势（DP）结构的工作流程。一个
figure 1

周期始于创建初始培训数据集。b在训练步骤中，训练了四个具有不同初始参数的DP。c评估了训练有素的DPS的预测精度。d如果准确性不足，则会生成其他培训数据以改善模型。首先，使用当前DPS的分子动力学（MD）生成了多种多样的候选原子结构。在随后的筛选步骤中，根据DPS之间的最大力偏差选择结构。该偏离阈值设置为有效地识别出具有较大预测错误的学识渊博的结构。然后，评估所选候选者的结构相似性相对于当前的训练集，并选择具有低相似性的结构进行标记。在标签步骤中，在选定的结构上进行了密度功能理论（DFT）计算，并将所得数据添加到训练集中。重复此循环，直到获得具有令人满意的精度的DP。（RMSE：均方根错误）。

构建深厚潜力的精度

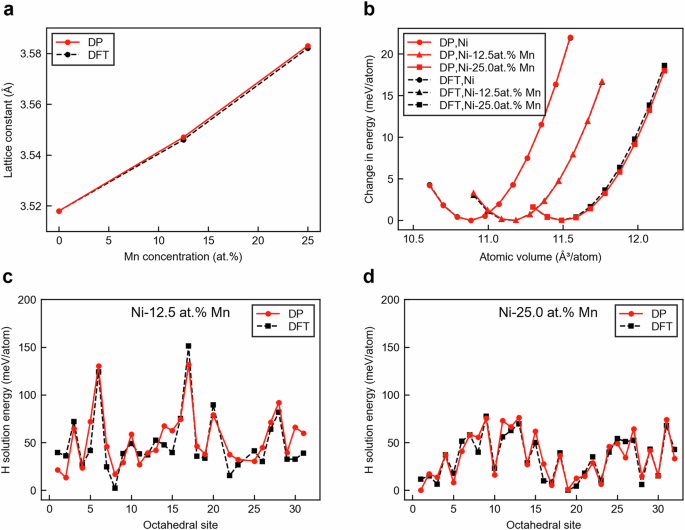
图 2A和b分别显示了Ni晶格常数对Mn浓度的依赖性，分别显示了晶格常数变化和能量之间的关系。如以下小节所述，MN的存在引起的晶格常数的变化显着影响通过激活能的氢扩散。为了获得准确性验证，我们在FCC结构中使用了2 2 2 −2â€2超级电池。因此，每个超级电池都包含32个八面体质的地点。在这里，我们采用了具有最高随机性的NiâMn合金构型，以最大程度的随机性来实现合金元素布置的验证。DP预测与DFT结果非常吻合。特别是，由于添加了MN而引起的Ni晶格扩展精确复制。图 2C和d分别在Niâ12.5at。％Mn和Niâ25.0at。％Mn中的每个八面体位点显示氢溶液能量。这些能量是氢扩散激活能的参考值。DPS成功地重现了位点之间氢溶液能量中的小能量差异。

图2：合金中Ni -MN随机合金和氢溶液的DP精度。一个
figure 2

Mn浓度对Ni晶格常数的影响。bNi和NiâMn合金中的原子体积与能量之间的关系。在b，能量参考设置为每个系统平衡晶格常数的能量。光盘Niâ12.5at。％Mn和Niâ0.25.0at。％Mn中的氢 - 溶解能的精度。为了c和d，DP训练数据集中不包括氢分子；因此，参考能不是分子中分离的氢原子的参考能，而是设置为最低计算的溶液能量。图 3

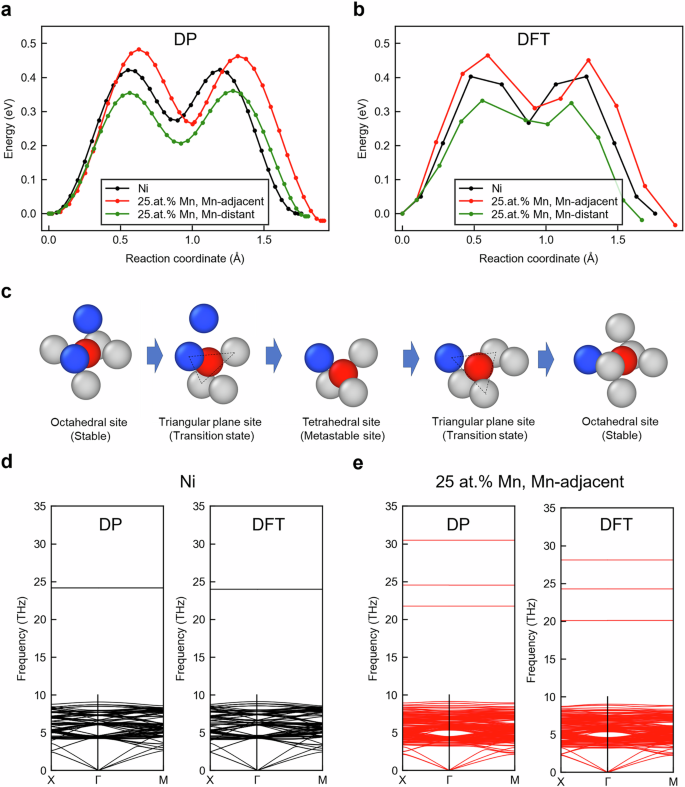
A和b显示与氢扩散相关的能量曲线，该氢扩散是使用裸弹性带（NEB）方法计算的85，，，，86（请参阅方法）分别使用DP和DFT，纯Ni和Niâ0.0 -at。％Mn。这些能量曲线是确定从MD模拟得出的氢扩散活化能量的主要因素。在基于DFT的NEB计算中，Niâat 25 at的SCF（自洽场）收敛有时需要几百个步骤，这与使用DP的NEB计算相比，需要使用减少的图像数量。SCF收敛所需的大量步骤可能与ni 25 at的磁性不稳定有关，其中Mn原子可能表现出铁磁或抗铁磁磁与周围的Ni原子，并且这些磁性状态的能量很接近43。应当指出的是，在训练数据集中，所有MN原子都被证实表现出铁磁耦合。

图3：Ni -MN随机合金中氢扩散的DP精度。
figure 3

使用的氢扩散的能量曲线一个DP和bDFT，对于纯Ni和Niâ0.0at。％Mn，比较了Mn原子在扩散屏障位点与氢相邻而不是氢的情况。c在相邻MN的情况下，扩散期间氢的局部原子构型。灰色，蓝色和红色球体分别代表Ni，Mn和H原子。灰色球代表Ni原子。在这里，扩散是从一个与两个Mn原子相邻的八个原子附近的八面体位点发生的。在过渡状态下，三个相邻的宿主金属原子之一是mn。d使用DP和DFT计算的Ni中占八面体位点的氢原子的声子分散。e使用DP和DFT计算的Niâ0.0.％Mn中占八面体位点的氢原子的声子分散。在d和e，该结构对应于稳定的构型，其中单个Mn原子与氢相邻，如图所示c。图 3C说明扩散过程中氢的局部原子环境。

氢扩散通过四面体部位进行，从稳定的八面体位点过渡到相邻的八面体位点。请注意，活化能对应于八人体和四面体部位之间的过渡期间氢最近的三个宿主原子的状态。此后，该状态称为过渡状态。纯Ni中的氢 - 扩散活化能由DP很好地复制，值分别从DP和DFT获得了0.41和0.40 eV。对于Niâ25.0at。％Mn，我们检查了两个代表性的案例，其中Mn的作用变得特别重要，如以下小节中详细讨论：（i）过渡态中与氢相邻的三个宿主原子之一为MN，并且（ii）所有三个均为Ni。在存在MN的情况下，激活能量增加。但是，当所有三个原子均为Ni时，激活能就会降低。DP准确地再现了Mn的效果。

图 3D和e在固体溶液中，用氢显示了纯ni和Niâ25.0at的纯Ni和Niâ25.0at的声子分散关系。这些图代表了八面体位点的声子分散，这对于准确计算氢扩散系数的指数前至关重要。44。在纯净的Ni中，当氢原子位于八面体间质位点时，声子分散体在大约24 thz处表现出三重归化的平坦带。该结果表明氢与宿主晶格薄弱。DP结果与从DFT计算获得的结果非常吻合，并有效地捕获了这种行为。

对于Niâ0.0at。％Mn，Mn原子与八面体位点相邻的情况，如图所示。 3C被考虑。计算表明，在八面体位置的MN存在下，氢氢表现出三种不同的振动模式。这种行为表明脱落率提升。如补充注释中所述 1，对于过渡态，DP在再现Mn诱导的效应方面所达到的精度低于纯Ni的精度。与纯Ni相比，合金系统中各种扩散途径的种类增加可能是由于这种较低的扩散途径，这使得过渡状态的足够采样更具挑战性。然而，DP定性地重现了MN的影响。总而言之，使用GenNIP4MD开发的DP成功再现了各种DFT结果，包括NiâMn合金的晶格常数和相关的能量变化，氢溶液溶液及其位点依赖性，氢 - 扩散激活能量和声子分散体。这些结果表明，获得的DP可以准确计算NiâMn合金中的氢扩散率。

使用DP和实验值计算的氢扩散系数的值的值

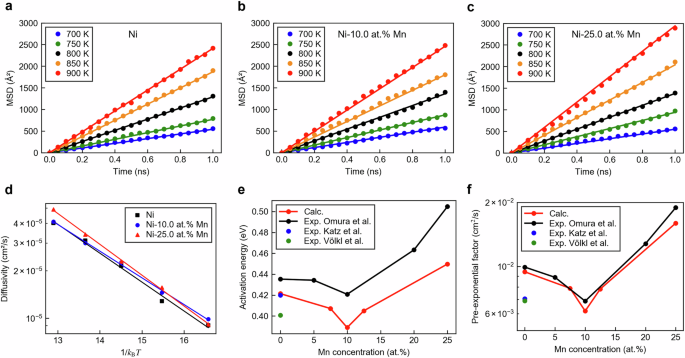
图 4a，b和C显示了使用开发的DP用于纯Ni，Ni-10.0 at。％Mn和Ni-25.0 at。％Mn进行的氢扩散的MD模拟示例。在所有系统中，时间与均方位移（MSD）之间都存在线性关系，并验证了与爱因斯坦方程式的拟合（请参阅方法）。图 4d呈现从爱因斯坦关系在每个温度下获得的扩散系数的Arrhenius图。这些图的线性性验证了使用单个激活能进行拟合的方法。这种一致性还验证了氢扩散分析中使用的计算条件和原子结构模型。其他化学成分获得了相似的结果。有关详细信息，请参阅补充说明 2。

图4：NiâMn合金中计算出的和实验性氢扩散系数的比较。
figure 4

A c退火时间与平方平方位移（MSD）之间的关系一个妮，bniâ10.0at。％mn和cniâ25.0at。％mn。d氢扩散系数的Arrhenius图与1/kbt对于这三个系统。E，fMN含量对计算的和实验效应的比较e激活能和fNi氢扩散的指数率因子。Omura等人报告的实验结果。42，Katz等。87和Vã¶lkl等。88显示参考。图 4e和f

呈现每个系统获得的氢扩散前指数因子和激活能。为了进行比较，Omura等人报告的实验结果。42，Katz等。87和Vã¶lkl等。88也提出。关于激活能，对于纯Ni，从MD计算中获得的激活能为0.42âEV，这与图所示的0.41 eV的八面体到八面体激活能非常吻合。 3。请注意，氢 - 扩散活化能通常与NEB分析计算得出的氢相对应44，，，，47。该结果进一步验证了MD模拟中使用的计算设置和结构模型。计算为无MN病例的0.42 eV的值略低于Omura等人报道的0.44 eV值。42;但是，当考虑Katz等人报告的值时，差异在实验不确定性范围内。87和Vã¶lkl等。88。此外，Wimmer等。44理论上使用基于第一原理方法的声子计算和过渡状态理论从理论上估算了Ni中的氢扩散系数。他们估计，零点振动为激活能贡献了约0.02 eV。该值与Omura等人的实验结果差异很好。42，这表明在当前MD模拟中获得的激活能的轻微偏差可能会出现，因为零点振动贡献不能反映在MD计算中。对于MN附加系统，激活能的绝对值略低于实验值。但是，随着MN含量增加的变化趋势得到了准确的再现。具体而言，在向纯Ni中添加〜10.0 at。％Mn，激活能量略微降低，然后升至25.0 at。％％％，紧密地重现了实验中观察到的趋势。关于指数前因子，计算值与Omura等人的实验结果一致。42。该协议的一个可能原因是，在MD计算中未明确包含的零点振动效应对指数前因子只有很小的影响44。此外，由于添加了MN，因此在模拟中准确地重现了指数前因子的非线性变化。总而言之，本研究中开发的DP与MD模拟相结合，实现了MN添加对Ni氢扩散率的影响的定量繁殖。特别是，这种方法成功地捕获了MN含量对氢扩散系数的非线性效应。

Mn添加对Ni氢扩散作用的原子级机制

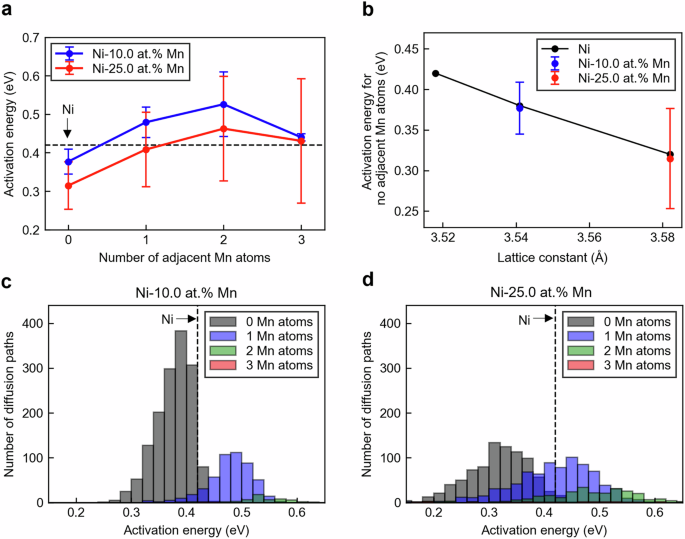
我们探索了MN添加会影响氢扩散的原子尺度机制。根据Omura等人的实验结果。42，工业重要性的扩散系数接近室温，主要受激活能的控制。例如，在270°C下，由于活化能的增加，Niâ25.0 -at。ni 25.0的氢扩散率显着降低，大约达到了纯Ni的一半。因此，本节侧重于MN添加对氢扩散活化能的影响。如图所示 3，过渡态中相邻Mn原子的存在会显着影响氢 - 扩散活化能。为了详细研究这种效果，我们构建了一个4特殊的准随机结构（SQS）模型89（请参阅方法）包括256个宿主金属原子，用于Niâ10.0at。％Mn和Niâ25.0 at。％Mn，分别显示出最小和最大激活能。然后，我们使用DP和NEB方法计算了所有256-可能的扩散路径的激活能。图 5a显示活力与过渡态相邻Mn原子数量的函数。在这两个系统中，活化能都随着相邻Mn原子数量的增加而增加。这种趋势可以归因于在相同键长的Ni -h的核心核心排斥力较强的趋势43，这与Mn的原子半径大于Ni的事实是一致的。当Mn原子位于过渡状态附近时，这种排斥的相互作用会导致能量增加，那里的宿主金属之间的原子间距离变短。

图5：MN对Ni氢扩散活化能的影响。一个
figure 5

相邻Mn原子的数量与ni-10.0 at。％Mn和Niâ25.0 at。％Mn中的氢扩散活化能之间的关系。b零相邻Mn原子的晶格常数与活化能之间的关系。还显示了通过改变纯Ni晶格常数获得的趋势以进行比较。光盘Niâ10.0At的激活能的直方图分别为。％Mn和Niâ0.5.0at。％Mn。面板中的结果A从4 4â€4超级细胞中的256个宿主金属原子的SQS模型获得。纯Ni中的氢扩散活化能由虚线表示。

另一方面，当过渡状态下没有相邻的Mn原子时，Ni -10.0 at。at。at。％和ni -25.0 at。％mn的平均激活能为0.38和0.32 eV，这两个ev均为。％mn，两者均低于pure ni（0.41 -ev）。为了解释这一结果，图 5b当相邻Mn原子的数量为零时，显示活化能与晶格常数之间的关系。这种关系与与各种晶格常数的纯NI观察到的趋势非常吻合。这些结果表明，在没有相邻的Mn原子的情况下，由于添加MN而引起的晶格扩展引起的活化能会增加，从而增加了宿主原子与宿主原子与氢之间的距离，从而减少了核心压力的能量损失。从这些发现中，添加了MN对氢扩散的两个主要影响：（i）由于Ni晶格的扩展而引起的活化能量降低，以及（ii）由排斥Mn的相互作用引起的激活能量增加。

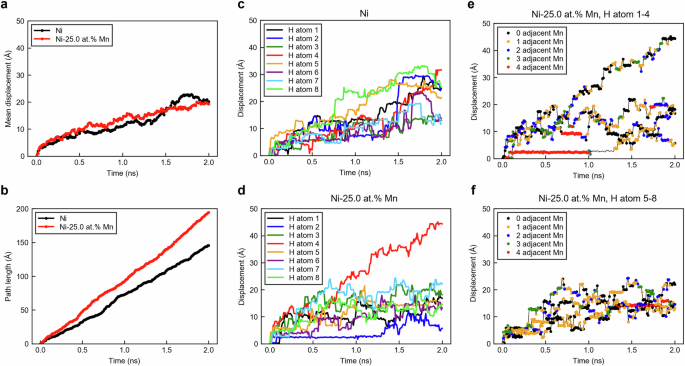
接下来，我们考虑了这两种影响对氢扩散行为的贡献。图 5C和d显示了分别显示Niâ10.0at。％和Ni-25.0 at的氢扩散活化能的直方图。For the Ni–25.0 at.% Mn, the number of diffusion paths occurring with increased activation energy was almost identical to those arising for decreased activation energy, relative to pure Ni.Therefore, selective diffusion of hydrogen over long distances via only those paths in which the activation energy is reduced owing to lattice expansion is difficult.Consequently, the effective activation energy may exceed that of pure Ni.To verify this, Fig. 6shows one representative case (i.e., the average over eight hydrogen atoms in a single configuration of alloying elements and hydrogen positions) for both pure Ni and Ni–25.0 at.% Mn at 700 K, in which the average MSD is close to the overall average among multiple cases shown in Fig. 4A和c。图 6A和bpresent the time evolution of the path length (cumulative distance traveled) and mean displacement (the square root of the MSD, i.e., the straight-line distance between the initial and final positions) of hydrogen.A temperature of 700 K was chosen because the host-metal thermal vibrations were relatively moderate, which facilitated atomic structure analysis.In both systems, the hydrogen diffusion behavior was well described by a single activation energy value;thus, there was no loss of generality when the analysis was conducted at 700 K.As shown in Figs. 4A和4C, at 700 K, the MSD and its square root (i.e., the mean displacement) of pure Ni and Ni–25.0 at.% Mn (Fig. 6a) were similar.However, the path length of the latter was longer (Fig. 6b）。This outcome indicates that hydrogen tends to follow longer diffusion paths in Ni–25.0 at.% Mn, selecting routes with reduced activation barriers due to the increased lattice constant resulting from Mn addition.

Fig. 6: Hydrogen diffusion behavior in Ni and Ni–25.0 at.% Mn.一个
figure 6

Time evolution of average hydrogen-atom displacement (i.e., square root of MSD), andbtime evolution of hydrogen-atom cumulative path lengths in Ni and Ni–25.0 at.% Mn.Results are shown for a single case at 700 K for which the average displacement closely matched the mean value across multiple cases shown in Fig. 4。光盘Displacements of eight individual hydrogen atoms in case shown inb, for Ni and Ni–25.0 at.% Mn, respectively.e，，，，fDisplacements of eight hydrogen atoms in Ni–25.0 at.% Mn, color-coded by number of Mn atoms adjacent to octahedral site occupied by each hydrogen atom at a given time.图 6C和d

show the mean displacements of the individual hydrogen atoms.In the pure Ni, monotonic increases in the displacements of almost all hydrogen atoms occurred with increasing annealing time.In contrast, for the Ni–25.0 at.% Mn, although the mean displacements of some hydrogen atoms increased significantly, for the majority of hydrogen atoms, the mean displacements tended to increase gradually with repeated increases and decreases.To further elucidate the influence of Mn on the hydrogen diffusion, the path lengths of each hydrogen atom in Ni–25.0 at.% Mn are shown in Fig. 6E和f, color-coded by the number of adjacent Mn atoms at the octahedral sites through which the hydrogen diffused.These results indicate that most hydrogen atoms underwent diffusion primarily via sites adjacent to Mn atoms, demonstrating that Mn significantly impacts the selection of diffusion pathways.These findings suggest that, in long-range hydrogen diffusion, hydrogen rarely moves exclusively through low-barrier paths.That is, in most cases, hydrogen must also traverse high-barrier paths.This behavior likely contributes to the increased effective activation energy observed in Ni–25.0 at.% Mn compared to that of pure Ni.Moreover, when four Mn atoms are adjacent to an octahedral site, the hydrogen interacts directly with the Mn regardless of the surrounding tetrahedral site to which it attempts to move, yielding a high activation energy and a prolonged stay at that site.Thus, hydrogen trapping at octahedral sites surrounded by adjacent Mn atoms may also contribute to the increase in the effective activation energy caused by Mn addition.As demonstrated above, the addition of Mn induces two opposing effects on the hydrogen-diffusion activation energy: a decrease owing to the Ni lattice expansion, and an increase owing to repulsive Mn–H interactions.Based on simple combinatorial calculations, the fractions of diffusion paths involving adjacent Mn atoms in the transition state were found to be 27.1% and 57.8% for 10.0 at.% Mn and 25.0 at.% Mn, respectively.Thus, the number of paths involving repulsive Mn–H interactions increases with the Mn content.Consequently, for Ni–10.0 at.% Mn, the reduction in activation energy due to lattice expansion dominates, lowering the effective activation energy compared to that of pure Ni.In contrast, for Mn content exceeding 10 at.%, the repulsive Mn–H interactions have a more pronounced effect, and at 25.0 at.% Mn, the effective activation energy increases.Finally, we discuss the effect of the Mn addition on the pre-exponential factor.As mentioned previously, the qualitative behavior of the pre-exponential factor as a function of the Mn content mirrors that of the activation energy.That is, the pre-exponential factor decreases when approximately 10 at.% Mn is added to Ni, and then increases again up to 25.0 at.%, indicating a non-linear trend.Although changes in the lattice constant influence the jump distance (scaling with the square of the lattice parameter), the resulting change in the pre-exponential factor between that of pure Ni and Ni–25.0 at.% Mn is only approximately 4%.This difference is insufficient to explain the observed 1.69-fold increase in the pre-exponential factor.Therefore, the effect of the lattice expansion on the pre-exponential factor via the jump distance is likely limited, with other factors being dominant.

As shown in Fig. 3e, diffusion paths involving adjacent Mn atoms in the transition state cause degeneracy of the octahedral stable site, and the transition state is lifted, which causes the emergence of higher-frequency vibrational modes.However, lattice expansion softens phonon modes, thereby reducing the jump frequency.Qualitatively, these two effects explain the dependence of the pre-exponential factor on the Mn content.However, for a more quantitative discussion, a comprehensive and detailed analysis of the effects of the alloy element distribution on the phonon dispersion is required, which we leave for future work.

Application of findings from this study

This study elucidated the mechanisms through which the addition of Mn affects hydrogen diffusion in Ni.Two primary effects of Mn addition were identified: a decrease in activation energy due to expansion of the Ni lattice constant and an increase in activation energy due to repulsive Mn–H interactions.These two effects are not unique to Mn;rather, they represent general mechanisms exhibited by alloying elements in randomly distributed face-centered cubic (fcc) metals.These insights are valuable for interpreting the influences of various alloying elements on hydrogen diffusion.Omura et al.42experimentally investigated the effects of Mn and Cr on hydrogen diffusivity, and showed that, at an addition level of 20 at.%, Cr generated a greater increase in the hydrogen-diffusion activation energy than Mn.As Cr and Mn are neighboring elements in the periodic table, with similar core repulsion characteristics, this difference can be interpreted as being due to the smaller lattice expansion effect induced by Cr compared to that of Mn when both elements are at the same concentration.Thus, the findings of the present study can be broadly applied to other alloying elements, to interpret their effects on hydrogen diffusion.In this study, we used GeNNIP4MD to construct an MLIP for the Ni–Mn–H system and demonstrated that the resulting MD simulations successfully reproduced the experimentally observed hydrogen-diffusion trends in Ni–Mn alloys.This study demonstrates the effectiveness of MLIP construction using GeNNIP4MD for metallic materials and illustrates potential applications in computational materials science enabled by the construction of high-accuracy ternary MLIPs.Although our focus was on the Ni–Mn system, the proposed approach is applicable to hydrogen diffusion in a wide range of binary random alloys.Therefore, this technique can potentially predict the effects of alloying elements on hydrogen diffusion in diverse alloy systems, without experimental measurements.At present, MLIP construction and MD simulations based on those MLIPs require considerable computational resources and, in some cases, may even be costlier than experiments.However, as computation performance is continuously improving, this approach is expected to become a powerful tool for the design of hydrogen-resistant materials.

方法

MLIP-based calculation of hydrogen-diffusion coefficient

Using the MLIP constructed according to the procedure described in the “Overview of MLIP construction using GeNNIP4MD” section, hydrogen-diffusion coefficients were calculated for pure Ni, Ni–7.5 at.% Mn, Ni–10.0 at.% Mn, Ni–12.5 at.% Mn, and Ni–25.0 at.% Mn to span the compositional range reported in the experimental study of Omura etal。42。Diffusion simulations were performed using supercells comprising 2048 host metal atoms, which were created by expanding the conventional fcc unit cell to a size of 8 × 8 × 8, as illustrated in Fig. 7。The OVITO software package90was used for the atomic structure visualization.

Fig. 7: Atomic structures used in MD simulations for the prediction of hydrogen diffusion coefficients.
figure 7

a–cRepresentative atomic configurations for Ni, Ni–10.0 at.% Mn, and Ni–25.0 at.% Mn, respectively.The gray, blue, and red spheres represent Ni, Mn, and H atoms, respectively.

In alloy systems, owing to the constraints on the supercell size and annealing time, the results may depend on the alloying-element arrangement.Therefore, in this study, multiple configurations were used for each composition.To represent random alloy configurations with the maximum possible accuracy, an SQS model89was employed.This model was also used in previous DFT studies of hydrogen solubility in random Ni alloys43。Note that this method determines near-random atomic arrangements in small supercells based on correlation functions that quantify the randomness.Here, SQSs were generated using the alloy-theoretic automated toolkit (ATAT)91and its mcsqs code92。The generation criteria employed in this work were adopted from previous studies43，，，，93。Among the many generated SQSs, those with the best correlation function values were selected.For each composition, i.e., Ni–7.5 at.% Mn, Ni–10.0 at.% Mn, Ni–12.5 at.% Mn, and Ni–25.0 at.% Mn, 5, 5, 5, and 6 supercells with SQS-based random alloy configurations were used, respectively.Eight hydrogen atoms were randomly placed at octahedral sites in each supercell to generate the initial structures for the diffusion calculations.This hydrogen content corresponded to approximately 140 wt ppm, which is of the same order as the hydrogen concentration under a hydrogen pressure of 100 MPa employed in the experiment by Omura et al.42。Owing to the high computational cost of the MLIP, the placement of eight hydrogen atoms yielded statistically meaningful results with a limited number of simulations.For the pure Ni, the simulations were performed on 25 different systems with various initial hydrogen configurations.For each Ni-Mn alloy configuration, five different initial hydrogen placements were simulated, which yielded more than 25 combinations for each composition.The simulation conditions were based on a previous study on Ni47, and all calculations were performed under periodic boundary conditions.Temperatures of 700, 750, 800, 850, and 900 K were selected to ensure sufficient hydrogen diffusion and statistical convergence of the diffusion coefficient within the MD simulation duration.First, a 50-ps annealing process was performed using a Nosé–Hoover thermostat at the target temperature, with the pressure controlled at 0 to relax the initial structures.Subsequently, a 1.0-ns annealing process was conducted to enable computation of the diffusion coefficients.A 0.5-fs time step was used.Following the approach of Torres et al.47, the hydrogen-atom MSD during annealing was computed, and the diffusion coefficients at each temperature were obtained using the Einstein relation.Furthermore, the pre-exponential factor and activation energy were derived from Arrhenius plots of the diffusion coefficients against temperature.As discussed in the Results section, the hydrogen diffusion behaviors in all the alloy systems were well described by the Einstein relation across multiple alloy configurations and initial hydrogen placements.The Arrhenius plots revealed linear trends that were well fitted when a single diffusion coefficient was used for each alloy system.

MLIP construction using GeNNIP4MD

To train the DP models on the initial dataset and for each iterative training step, we used DeePMD-kit (version 2.2.8)94。The model architecture and hyperparameters were set based on a previous study on W–H DP construction using DP-GEN95。In detail, we employed DP models using a two-body embedding descriptor (i.e., se_e2_a).The cutoff radius was set to 6.5 Å, the embedding net comprised layers with 20, 40, and 80 neurons, and the number of axis neurons was 16. The fitting network had three hidden layers with 240 neurons each, and the learning rate began at 1×10−3and decayed to 1.0 × 10−8over 800,000 training steps.The deep neural network architecture comprised three fully connected hidden layers, each containing 240 neurons, and the activation function was set to a hyperbolic tangent for all hidden layers.

The structures used to construct the initial and additional training datasets were selected to span the atomic environments encountered during MD simulations for hydrogen diffusivity calculations.Specifically, we employed atomic structures from the initial dataset, as listed in Table 1。The initial training dataset comprised three subsets: (1) pure Ni with hydrogen in a solid solution, (2) a random Ni–12.5 at.% Mn alloy with hydrogen in solid solution, and (3) a random Ni–25.0 at.% Mn alloy with hydrogen in solid solution.All these were based on 2 × 2 × 2 supercells with 32 host metal atoms in the fcc structure, into which 0–2 hydrogen atoms were introduced in solid solution.The atomic structures of (2) and (3) were generated using the SQS approach described in the previous section.In the initial dataset, only one random configuration was used for each chemical composition.In addition to the equilibrium volume, structures expanded by 2.0% were also prepared.For each of these, ab initio MD (AIMD) simulations were performed for 200 steps at 600 and 1200 K under constant-volume conditions, and snapshots were extracted at two-step intervals and included in the initial dataset.Similarly, AIMD simulations under NPT conditions were performed at 600 and 1200 K using the equilibrium volumes, and snapshots were again extracted at every step and included in the initial dataset.Furthermore, for the atomic structures in (2) and (3), we placed one hydrogen atom in each of the 32 octahedral sites and performed structural relaxation.Five snapshots were extracted from each relaxation trajectory and included in the dataset.All spin-polarized DFT calculations for the initial dataset were performed under the conditions described in the “Computational details” subsection.The energies, forces, and virial tensors of each structure were computed.As this study aimed to accurately evaluate hydrogen diffusion, additional training data were constructed using structures similar to those of the initial dataset (see Table 1）。To generate these additional structures, MD simulations using DPs were conducted using LAMMPS96。For random Ni–12.5 at.% Mn and Ni–25.0 at.% Mn alloys with hydrogen in solid solution, multiple SQS models were generated to sample diverse alloy configurations.Among these, four and nine additional random configurations, respectively, were selected based on the high degrees of randomness in their correlation functions.We also included structures with volumes compressed by 1.0% and 0.5% and expanded by 0.5%, 1.0%, 1.5%, and 2.0%, to reflect the thermally expanded environments relevant to hydrogen diffusion during the MD simulations.Annealing-based sampling was performed on these structures using NVT ensembles at 300, 600, 900, and 1000 K for 50 ps.Owing to the small 2 × 2 × 2 supercell and the instability introduced by the high hydrogen concentrations during long NPT runs, we opted for NVT simulations with fixed volumes.A 0.5-fs time step was used, and structures were extracted every 100 steps as candidate configurations.In these simulations, one of four trained DP models was employed.In the subsequent screening step, for each structure, the maximum deviation in the predicted atomic forces among the four DP models, which were trained with the same hyperparameters but different random seeds, was calculated.Structures with a deviation between 0.10 and 0.25 eV/Ã… were selected as candidates for labeling.Next, structures for labeling were selected based on their similarities.In detail, multidimensional features extracted from the hidden layers of the DP models were projected onto a two-dimensional space using densMAP97, and the pairwise Euclidean distances between the candidate structures in this 2D space were computed.To enable selection of a fixed number of representative structures, those with shorter distances from others were sequentially removed until the desired number of 900 structures remained in each screening round.The DFT calculations for labeling, including spin polarization, were performed under the same conditions as those described in the Computational Details section for the atomic structures selected through the screening process.The energies, forces, and virial tensors of each structure were calculated.

Table 1 Training datasets and fitting errors of the constructed deep potentials

Following convergence of the GeNNIP4MD iterative workflow, the MLIP was trained for the final time using the accumulated dataset.Twenty iterations were performed.The DP architecture used during the iterations was retained, with only the number of training steps being changed;that is, the training steps were increased to two million.However, no significant improvement in the fitting accuracy was observed compared to the case with 800,000 steps, which confirmed that sufficient convergence during training had already been attained.The final training dataset comprised 17,777 structures (592,435 local atomic environments).As details in Table 1, the root mean square errors (RMSEs) for the energy and force were 5.70 meV/atom and 68.41 meV/Ã…, respectively, indicating sufficient accuracy.We also tested a hybrid descriptor combining 2- and 3-body (se_e2_a and se_e3, respectively) embedding terms56, following a previous study on W–H DP development95;however, we observed no significant improvement in fitting accuracy (Supplementary Note 3）。Therefore, for computational efficiency in MD simulations requiring long timescales and a large number of cases, we employed a 2-body embedded descriptor DP model.

Computational details

Spin-polarized DFT calculations were performed to construct the training dataset and validate the accuracy of the interatomic potential using the projector augmented wave (PAW) method, as implemented in VASP98，，，，99。The exchange-correlation potential was treated using the generalized gradient approximation with the Perdew–Burke–Ernzerhof functional100。The pseudopotentials for Ni and Mn include 4 s and 3 d electrons as valence electrons;these choices were consistent with those used in our previous DFT calculations43。The plane-wave cut-off energy was set to 500 eV.The k-point mesh for each atomic structure was generated using the Monkhorst–Pack scheme101, and was chosen to match the accuracy of an 8×8×8 mesh for the conventional unit cell of Ni.This setup corresponded to a KSPACING of 0.13 in VASP and ensured an accuracy equal to or higher than that adopted in previous studies on MLIP development65，，，，67。For improved convergence, the Methfessel–Paxton smearing method102with a 0.1-eV smearing width was employed.The convergence criterion for the self-consistent electronic calculations was set to 10−6eV for the total energy.Structural relaxations were performed until the forces on each atom were less than 10−2eV/Ã….All DP-based calculations for accuracy verification were performed using LAMMPS96。AIMD simulations for construction of the initial training dataset were performed using Parrinello–Rahman dynamics103，，，，104with a Langevin thermostat.A 0.5-fs time step was used in the AIMD simulations.To analyze the hydrogen-diffusion transition states, the transition paths between the initial and final atomic configurations were determined using the climbing-image NEB (CI-NEB) method85，，，，86。Phonon dispersion was calculated using the Phonopy package105，，，，106。

数据可用性

The data that support the findings of this study are available from the corresponding author, K.I., upon reasonable request.The data are not publicly available due to restrictions imposed by Nippon Steel Corporation;access may be granted only with permission from the company.

代码可用性

The main codes utilized in this study—DeePMD-kit94, LAMMPS96—are open-source and can be accessed online, with their licensing information and user manuals detailed in the respective references.GeNNIP4MD75is proprietary software and is not open-source;however, the code may be made available upon reasonable request.Requests for access should be directed to fj-mi-tech-contact@dl.jp.fujitsu.com.

参考

  1. Winsche, W. E., Hoffman, K. C. & Salzano, F. J. Hydrogen: its future role in the nation’s energy economy.科学 180, 1325–1332 (1973).

    PubMed一个 Google Scholar一个 

  2. Ouyang, L., Jiang, J., Chen, K., Zhu, M. & Liu, Z. Hydrogen production via hydrolysis and alcoholysis of light metal-based materials: a review.Nanomicro Lett. 13, 134 (2021).

    PubMed一个 PubMed Central一个 Google Scholar一个 

  3. Yap, J. & McLellan, B. Evaluating the attitudes of Japanese society towards the hydrogen economy: A comparative study of recent and past community surveys.int。J. Hydrog.活力，，，，https://doi.org/10.1016/j.ijhydene.2023.05.174（2023）。

  4. Kim, C. et al.Review of hydrogen infrastructure: The current status and roll-out strategy.int。J. Hydrog.活力 48, 1701–1716 (2023).

    Google Scholar一个 

  5. Peng, Z. et al.Overview of hydrogen compression materials based on a three-stage metal hydride hydrogen compressor.J.合金。compd。 895, 162465 (2022).

    Google Scholar一个 

  6. Elvira, K. et al.Hydrogen technology for supply chain sustainability: The Mexican transportation impacts on society.int。J. Hydrog.活力 47, 29999–30011 (2022).

    Google Scholar一个 

  7. Liu，J。等。A comprehensive review on hydrogen permeation barrier in the hydrogen transportation pipeline: Mechanism, application, preparation, and recent advances.int。J. Hydrog.活力 101, 504–528 (2025).

    Google Scholar一个 

  8. Yu, H. et al.Hydrogen embrittlement as a conspicuous material challenge─comprehensive review and future directions.化学修订版 124, 6271–6392 (2024).

    PubMed一个 PubMed Central一个 Google Scholar一个 

  9. Li，X。等。Review of the hydrogen embrittlement and interactions between hydrogen and microstructural interfaces in metallic alloys: Grain boundary, twin boundary, and nano-precipitate.int。J. Hydrog.活力 72, 74–109 (2024).

    Google Scholar一个 

  10. Meda, U. S., Bhat, N., Pandey, A., Subramanya, K. N. & Lourdu Antony Raj, M. A. Challenges associated with hydrogen storage systems due to the hydrogen embrittlement of high strength steels.int。J. Hydrog.活力 48, 17894–17913 (2023).

    Google Scholar一个 

  11. Sun, B. et al.Current challenges and opportunities toward understanding hydrogen embrittlement mechanisms in advanced high-strength steels: a review.Acta Metall.罪。 34, 741–754 (2021).

    Google Scholar一个 

  12. Pramuanjaroenkij, A. & Kakaç, S. The fuel cell electric vehicles: The highlight review.int。J. Hydrog.活力 48, 9401–9425 (2023).

    Google Scholar一个 

  13. Sasaki, K. et al.Hydrogen energy engineering。(Springer, 2016).

  14. Hirth, J. P. Effects of hydrogen on the properties of iron and steel.金属。反式。一个 11, 861–890 (1980).

    Google Scholar一个 

  15. Ordin, P. M. Safety Standard for Hydrogen and Hydrogen Systems Guidelines for Hydrogen System Design, Materials Selection, Operations, Storage and Transportation.NASA Technical Report（1997）。

  16. Gangloff, R. P. & Somerday, B. P.Gaseous hydrogen embrittlement of materials in energy technologies: mechanisms, modelling and future developments。(Elsevier, 2012).

  17. Nagumo, M.Fundamentals of hydrogen embrittlement。卷。921 (Springer, 2016).

  18. Jemblie, L. et al.Safe pipelines for hydrogen transport.int。J. Hydrog.活力 https://doi.org/10.1016/j.ijhydene.2024.06.309（2024）。

    Google Scholar一个 

  19. Okuno, K. & Takai, K. Extraction of reversible hydrogen trapped on prior austenite grain boundaries and promoting intergranular fracture in the elastic region of tempered martensitic steel by utilizing frozen-in hydrogen distribution at −196°C.Acta Mater。 259, 119291 (2023).

    Google Scholar一个 

  20. Rodoni, E., Claeys, L., Depover, T. & Iannuzzi, M. Effect of nickel on the hydrogen diffusion, trapping and embrittlement properties of tempered ferritic-martensitic dual-phase low alloy steels.int。J. Hydrog.活力 98, 418–428 (2025).

    Google Scholar一个 

  21. Li, H., Lee, C., Venezuela, J., Kim, H.-J.& Atrens, A. Hydrogen diffusion and hydrogen embrittlement of a 1500 MPa hot-stamped steel 22MnB5 in different austenitizing conditions.母校。科学。Eng., A 897, 146349 (2024).

    Google Scholar一个 

  22. Park, H. et al.Impact of hydrogen embrittlement on the tensile-shear property of resistance spot-welded advanced high-strength martensitic steels.int。J. Hydrog.活力 71, 319–333 (2024).

    Google Scholar一个 

  23. Matsunaga, H., Yamabe, J., Takakuwa, O., Ogawa, Y. & Matsuoka, S.Hydrogen Gas Embrittlement: Mechanisms, Mechanics, and Design。(Elsevier, 2024).

  24. Matsuoka, S., Yamabe, J. & Matsunaga, H. Criteria for determining hydrogen compatibility and the mechanisms for hydrogen-assisted, surface crack growth in austenitic stainless steels.工程。分数。机械。 153, 103–127 (2016).

    Google Scholar一个 

  25. Takakuwa, O., Yamabe, J., Matsunaga, H., Furuya, Y. & Matsuoka, S. Comprehensive understanding of ductility loss mechanisms in various steels with external and internal hydrogen.金属。母校。反式。一个 48, 5717–5732 (2017).

    Google Scholar一个 

  26. Sezgin, J.-G., Takakuwa, O., Matsunaga, H. & Yamabe, J. Simulation of the effect of internal pressure on the integrity of hydrogen pre-charged BCC and FCC steels in SSRT test conditions.工程。分数。机械。 216, 106505 (2019).

    Google Scholar一个 

  27. San Marchi, C. et al.Effect of microstructural and environmental variables on ductility of austenitic stainless steels.int。J. Hydrog.活力 46, 12338–12347 (2021).

    Google Scholar一个 

  28. Takaki, S. et al.Determination of hydrogen compatibility for solution-treated austenitic stainless steels based on a newly proposed nickel-equivalent equation.int。J. Hydrog.活力 41, 15095–15100 (2016).

    Google Scholar一个 

  29. Hughes, L. A., Somerday, B. P., Balch, D. K. & San Marchi, C. Hydrogen compatibility of austenitic stainless steel tubing and orbital tube welds.int。J. Hydrog.活力 39, 20585–20590 (2014).

    Google Scholar一个 

  30. San Marchi, C., Michler, T., Nibur, K. A. & Somerday, B. P. On the physical differences between tensile testing of type 304 and 316 austenitic stainless steels with internal hydrogen and in external hydrogen.int。J. Hydrog.活力 35, 9736–9745 (2010).

    Google Scholar一个 

  31. Zhang, L., Wen, M., Imade, M., Fukuyama, S. & Yokogawa, K. Effect of nickel equivalent on hydrogen gas embrittlement of austenitic stainless steels based on type 316 at low temperatures.Acta Mater。 56, 3414–3421 (2008).

    Google Scholar一个 

  32. Michler, T., Yukhimchuk, A. A. & Naumann, J. Hydrogen environment embrittlement testing at low temperatures and high pressures.Corros.科学。 50, 3519–3526 (2008).

    Google Scholar一个 

  33. Cho, H.-J., Cho, Y. & Kim, S.-J.Hydrogen embrittlement susceptibility of Cu bearing cost-effective austenitic stainless steels.int。J. Hydrog.活力 60, 1–10 (2024).

    Google Scholar一个 

  34. An, X. et al.Mechanisms of hydrogen embrittlement resistances in FCC concentrated solid solution alloys.Corros.科学。 229, 111894 (2024).

    Google Scholar一个 

  35. Wada, K. et al.Hydrogen-induced degradation of SUS304 austenitic stainless steel at cryogenic temperatures.母校。科学。Eng., A 927, 147988 (2025).

    Google Scholar一个 

  36. Ito, T. et al.Role of solute hydrogen on mechanical property enhancement in Fe–24Cr–19Ni austenitic steel: An in situ neutron diffraction study.Acta Mater。 287, 120767 (2025).

    Google Scholar一个 

  37. Ogawa, Y. et al.Hydrogen, as an alloying element, enables a greater strength-ductility balance in an Fe-Cr-Ni-based, stable austenitic stainless steel.Acta Mater。 199, 181–192 (2020).

    Google Scholar一个 

  38. Claeys, L., Deconinck, L., Verbeken, K. & Depover, T. Effect of additive manufacturing and subsequent heat and/or surface treatment on the hydrogen embrittlement sensitivity of 316L austenitic stainless steel.int。J. Hydrog.活力 48, 36142–36157 (2023).

    Google Scholar一个 

  39. Álvarez, G., Harris, Z., Wada, K., Rodríguez, C. & Martínez-Pañeda, E. Hydrogen embrittlement susceptibility of additively manufactured 316L stainless steel: Influence of post-processing, printing direction, temperature and pre-straining.加法。制造。 78, 103834 (2023).

    Google Scholar一个 

  40. Yamabe, J., Takakuwa, O., Matsunaga, H., Itoga, H. & Matsuoka, S. Hydrogen diffusivity and tensile-ductility loss of solution-treated austenitic stainless steels with external and internal hydrogen.int。J. Hydrog.活力 42, 13289–13299 (2017).

    Google Scholar一个 

  41. Marchi, C. S., Somerday, B. P. & Robinson, S. L. Permeability, solubility and diffusivity of hydrogen isotopes in stainless steels at high gas pressures.int。J. Hydrog.活力 32, 100–116 (2007).

    Google Scholar一个 

  42. Omura, T., Yamamura, M., Ito, K., Yamabe, J. & Matsunaga, H. Effects of alloying-element addition on hydrogen diffusion and hydrogen absorption in Ni.ISIJ Int。65, 1402–1409 (2025).

  43. Ito, K., Yamamura, M., Omura, T., Yamabe, J. & Matsunaga, H. Effects of Cr, Mn, and Fe on the hydrogen solubility of Ni in high-pressure hydrogen environments and their electronic origins: An experimental and first-principles study.int。J. Hydrog.活力 50, 148–164 (2024).

    Google Scholar一个 

  44. Wimmer, E. et al.Temperature-dependent diffusion coefficients from ab initio computations: Hydrogen, deuterium, and tritium in nickel.物理。修订版b 77, 134305 (2008).

    Google Scholar一个 

  45. Zhou, X.-Y.等。Machine learning assisted design of FeCoNiCrMn high-entropy alloys with ultra-low hydrogen diffusion coefficients.Acta Mater。 224, 117535 (2022).

    Google Scholar一个 

  46. Shuang, F. et al.Decoding the hidden dynamics of super-Arrhenius hydrogen diffusion in multi-principal element alloys via machine learning.Acta Mater。 289, 120924 (2025).

    Google Scholar一个 

  47. Torres, E., Pencer, J. & Radford, D. D. Atomistic simulation study of the hydrogen diffusion in nickel.计算。母校。科学。 152, 374–380 (2018).

    Google Scholar一个 

  48. Shiihara, Y. et al.Artificial neural network molecular mechanics of iron grain boundaries.Scr.母校。 207, 114268 (2022).

    Google Scholar一个 

  49. Mortazavi, B. Recent advances in machine learning-assisted multiscale design of energy materials.ADV。能源母校。 15, 2403876 (2025).

    Google Scholar一个 

  50. Wang, F. et al.Atomic-scale simulations in multi-component alloys and compounds: A review on advances in interatomic potential.J. Mater.科学。技术。 165, 49–65 (2023).

    Google Scholar一个 

  51. Behler, J. Four generations of high-dimensional neural network potentials.化学修订版 121, 10037–10072 (2021).

    PubMed一个 Google Scholar一个 

  52. Unke, O. T. et al.Machine Learning Force Fields.化学修订版 121, 10142–10186 (2021).

    PubMed一个 PubMed Central一个 Google Scholar一个 

  53. Gong, X., Li, Z., Pattamatta, A. S. L. S., Wen, T. & Srolovitz, D. J. An accurate and transferable machine learning interatomic potential for nickel.社区。母校。 5, 157 (2024).

    Google Scholar一个 

  54. Fellman, A., Byggmästar, J., Granberg, F., Nordlund, K. & Djurabekova, F. Fast and accurate machine-learned interatomic potentials for large-scale simulations of Cu, Al and Ni.物理。牧师。 9, 053807 (2025).

  55. Wang, J. et al.Efficient moment tensor machine-learning interatomic potential for accurate description of defects in Ni-Al Alloys.物理。牧师。 9, 053805 (2025).

  56. Zhang, S., Meng, F., Fu, R. & Ogata, S. Highly efficient and transferable interatomic potentials for α-iron and α-iron/hydrogen binary systems using deep neural networks.计算。母校。科学。 235, 112843 (2024).

    Google Scholar一个 

  57. Meng, F.-S.等。A highly transferable and efficient machine learning interatomic potentials study of α-Fe–C binary system.Acta Mater。 281, 120408 (2024).

    Google Scholar一个 

  58. Zhang, L., Csányi, G., van der Giessen, E. & Maresca, F. Atomistic fracture in bcc iron revealed by active learning of Gaussian approximation potential.Npj Comput.母校。 9, 217 (2023).

    Google Scholar一个 

  59. Pitike, K. C. & Setyawan, W. Accurate Fe–He machine learning potential for studying He effects in BCC-Fe.J. Nucl。母校。 574, 154183 (2023).

    Google Scholar一个 

  60. Kotykhov, A. S. et al.Constrained DFT-based magnetic machine-learning potentials for magnetic alloys: a case study of Fe–Al.科学。代表。 13, 19728 (2023).

    PubMed一个 PubMed Central一个 Google Scholar一个 

  61. Meng, F.-S.等。General-purpose neural network interatomic potential for the $\ensuremath{\alpha}$-iron and hydrogen binary system: Toward atomic-scale understanding of hydrogen embrittlement.物理。牧师。 5, 113606 (2021).

    Google Scholar一个 

  62. Sun, H. et al.Molecular dynamics simulation of Fe-Si alloys using a neural network machine learning potential.物理。修订版b 107, 224301 (2023).

    Google Scholar一个 

  63. Dragoni, D., Daff, T. D., Csányi, G. & Marzari, N. Achieving DFT accuracy with a machine-learning interatomic potential: Thermomechanics and defects in bcc ferromagnetic iron.物理。牧师。 2, 013808 (2018).

    Google Scholar一个 

  64. Mori, H. & Ozaki, T. Neural network atomic potential to investigate the dislocation dynamics in bcc iron.物理。牧师。 4, 040601 (2020).

    Google Scholar一个 

  65. Ito, K., Yokoi, T., Hyodo, K. & Mori, H. Machine learning interatomic potential with DFT accuracy for general grain boundaries in α-Fe.Npj Comput.母校。 10, 255 (2024).

    Google Scholar一个 

  66. Ito, K. & Tabata, S. -i First-principles predictions of transition metal alloying effects on cohesive energy of prior austenite grain boundaries in high-strength steels.母校。Today Commun. 46, 112890 (2025).

    Google Scholar一个 

  67. Meng, F.-S.等。General-purpose neural network interatomic potential for the α-iron and hydrogen binary system: Toward atomic-scale understanding of hydrogen embrittlement.物理。牧师。 5, 113606 (2021).

    Google Scholar一个 

  68. Ito, K., Otaki, T., Hyodo, K., Yokoi, T. & Mori, H. Machine-learning potential reveals the origin of hydrogen embrittlement at general grain boundaries in α-Fe.18 July 2025, PREPRINT (Version 1) available at Research Squarehttps://doi.org/10.21203/rs.3.rs-7113724/v1（2025）。

  69. Sun, C. et al.A high-throughput molecular dynamics study with a machine-learning method on predicting diffusion coefficient of hydrogen in α-iron grain boundaries.母校。Today Commun. 44, 111997 (2025).

    Google Scholar一个 

  70. Angeletti, A. et al.Hydrogen diffusion in magnesium using machine learning potentials: a comparative study.Npj Comput.母校。 11, 85 (2025).

    Google Scholar一个 

  71. Kwon, H., Shiga, M., Kimizuka, H. & Oda, T. Accurate description of hydrogen diffusivity in bcc metals using machine-learning moment tensor potentials and path-integral methods.Acta Mater。 247, 118739 (2023).

    Google Scholar一个 

  72. Yu, F., Xiang, X., Zu, X. & Hu, S. Hydrogen diffusion in zirconium hydrides from on-the-fly machine learning molecular dynamics.int。J. Hydrog.活力 56, 1057–1066 (2024).

    Google Scholar一个 

  73. Szlachta, W. J., Bartók, A. P. & Csányi, G. Accuracy and transferability of Gaussian approximation potential models for tungsten.物理。修订版b 90, 104108 (2014).

    Google Scholar一个 

  74. Zhang，Y。等。DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models.计算。物理。社区。 253, 107206 (2020).

    Google Scholar一个 

  75. Matsumura, N. et al.Generator of neural network potential for molecular dynamics: constructing robust and accurate potentials with active learning for nanosecond-scale simulations.J. Chem。理论计算。 21, 3832–3846 (2025).

    PubMed一个 Google Scholar一个 

  76. Zhang, L. et al.在Proceedings of the 32nd International Conference on Neural Information Processing Systems4441–4451 (Curran Associates Inc., Montréal, Canada, 2018).

  77. Chen, C. & Ong, S. P. A universal graph deep learning interatomic potential for the periodic table.纳特。计算。科学。 2, 718–728 (2022).

    PubMed一个 Google Scholar一个 

  78. Deng, B. et al.CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling.纳特。马赫。Intell。 5, 1031–1041 (2023).

    Google Scholar一个 

  79. Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces.物理。莱特牧师。 98, 146401 (2007).

    PubMed一个 Google Scholar一个 

  80. Drautz, R. Atomic cluster expansion for accurate and transferable interatomic potentials.物理。修订版b 99, 014104 (2019).

    Google Scholar一个 

  81. Shapeev, A. V. Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials.Multiscale Model.模拟。 14, 1153–1173 (2016).

    Google Scholar一个 

  82. Bartók, A. P., Payne, M. C., Kondor, R. & Csányi, G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons.物理。莱特牧师。 104, 136403 (2010).

    PubMed一个 Google Scholar一个 

  83. Thompson, A. P., Swiler, L. P., Trott, C. R., Foiles, S. M. & Tucker, G. J. Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials.J. Comput。物理。 285, 316–330 (2015).

    Google Scholar一个 

  84. Yoshimoto, Y., Matsumura, N., Iwasaki, Y., Nakao, H. & Sakai, Y. Large-Scale, Long-Time Atomistic Simulations of Proton Transport in Polymer Electrolyte Membranes Using a Neural Network Interatomic Potential.arXiv preprint arXiv:2503.20412（2025）。

  85. Henkelman, G., Uberuaga, B. P. & Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths.J. Chem。物理。 113, 9901–9904 (2000).

    Google Scholar一个 

  86. Henkelman, G. & Jónsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points.J. Chem。物理。 113, 9978–9985 (2000).

    Google Scholar一个 

  87. Katz, L., Guinan, M. & Borg, R. J. Diffusion of H2, D2 and T2 in single-crystal Ni and Cu.物理。修订版b 4, 330–341 (1971).

    Google Scholar一个 

  88. Völkl, J. & Alefeld, G. inHydrogen in Metals I: Basic Properties(eds Alefeld, G. & Völkl, J.) 321–348 (Springer Berlin Heidelberg, 1978).

  89. Zunger, A., Wei, S. H., Ferreira, L. G. & Bernard, J. E. Special quasirandom structures.物理。莱特牧师。 65, 353–356 (1990).

    PubMed一个 Google Scholar一个 

  90. Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool.模型。模拟。垫。科学。工程。 18, 015012 (2010).

    Google Scholar一个 

  91. van de Walle, A., Asta, M. & Ceder, G. The alloy theoretic automated toolkit: A user guide.卡尔法 26, 539–553 (2002).

    Google Scholar一个 

  92. van de Walle, A. et al.Efficient stochastic generation of special quasirandom structures.卡尔法 42, 13–18 (2013).

    Google Scholar一个 

  93. Yang, S., Wang, Y., Liu, Z.-K.& Zhong, Y. Ab initio simulations on the pure Cr lattice stability at 0K: Verification with the Fe-Cr and Ni-Cr binary systems.卡尔法 75, 102359 (2021).

    Google Scholar一个 

  94. Zeng, J. et al.DeePMD-kit v2: A software package for deep potential models.J. Chem。物理。 159, 054801 (2023).

    PubMed一个 PubMed Central一个 Google Scholar一个 

  95. Wang, X.-Y.等。Deep neural network potential for simulating hydrogen blistering in tungsten.物理。牧师。 7, 093601 (2023).

    Google Scholar一个 

  96. Plimpton, S. Fast parallel algorithms for short-range molecular dynamics.J. Comput。物理。 117, 1–19 (1995).

    Google Scholar一个 

  97. Narayan, A., Berger, B. & Cho, H. Assessing single-cell transcriptomic variability through density-preserving data visualization.纳特。生物技术。 39, 765–774 (2021).

    PubMed一个 PubMed Central一个 Google Scholar一个 

  98. Kresse，G。＆Joubert，D。从Ultrasoft伪电势到投影仪增强波的方法。物理。修订版b 59, 1758–1775 (1999).

    Google Scholar一个 

  99. Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set.物理。修订版b 54, 11169–11186 (1996).

    Google Scholar一个 

  100. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple.物理。莱特牧师。 77, 3865–3868 (1996).

    PubMed一个 Google Scholar一个 

  101. Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations.物理。修订版b 13, 5188–5192 (1976).

    Google Scholar一个 

  102. Methfessel, M. & Paxton, A. T. High-precision sampling for Brillouin-zone integration in metals.物理。修订版b 40, 3616–3621 (1989).

    Google Scholar一个 

  103. Parrinello, M. & Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method.J. Appl。物理。 52, 7182–7190 (1981).

    Google Scholar一个 

  104. Parrinello, M. & Rahman, A. Crystal structure and pair potentials: a molecular-dynamics study.物理。莱特牧师。 45, 1196–1199 (1980).

    Google Scholar一个 

  105. Togo, A., Chaput, L., Tadano, T. & Tanaka, I. Implementation strategies in phonopy and phono3py.J. Condens.Matter Phys. 35, 353001 (2023).

    Google Scholar一个 

  106. Togo, A. First-principles Phonon Calculations with Phonopy and Phono3py.J. Phys。Soc。JPN。 92, 012001 (2022).

    Google Scholar一个 

下载参考

致谢

This work used computational resources of the Supercomputer Fugaku provided by Riken through the HPCI System Research Project (Project ID: hp230272, hp240280).This work was partly supported by Accompanying User Support Program (【23Z-03, 23Z-05, 24H1-01】, Support content:【porting of application program, execution performance tuning】) performed by Research Organization for Information Science and Technology.

作者信息

作者和隶属关系

  1. Advanced Technology Research Laboratories, Nippon Steel Corporation, 20-1, Shintomi, Futtsu city, Chiba, 293-8511, Japan

    Kazuma Ito

  2. Fujitsu Research, Fujitsu Limited, 4-1-1, Kamiodanaka, Nakahara-ku, Kawasaki, Kanagawa, 211-8588, Japan

    Naoki Matsumura, Yuto Iwasaki & Yasufumi Sakai

  3. Steel Research Laboratories, Nippon Steel Corporation, 20-1, Shintomi, Futtsu city, Chiba, 293-8511, Japan

    Misaho Yamamura & Tomohiko Omura

  4. Department of Mechanical Engineering, Fukuoka University, 8-19-1 Nanakuma, Jonan-ku, Fukuoka, 814-0180, Japan

    Junichiro Yamabe

  5. Department of Mechanical Engineering, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka, 819-0395, Japan

    Hisao Matsunaga

  6. Research Center for Hydrogen Industrial Use and Storage (HYDROGENIUS), Kyushu University, 744 Motooka, Nishi-ku, Fukuoka, 819-0395, Japan

    Hisao Matsunaga

  7. International Institute for Carbon-Neutral Energy Research (WPI-I2CNER), Kyushu University, 744 Motooka, Nishi-ku, Fukuoka, 819-0395, Japan

    Hisao Matsunaga

作者

  1. Kazuma Ito
  2. Naoki Matsumura
  3. Yuto Iwasaki
  4. Yasufumi Sakai
  5. Misaho Yamamura
  6. Tomohiko Omura
  7. Junichiro Yamabe
  8. Hisao Matsunaga

贡献

Kazuma Ito: Conceptualization, Methodology, Software, Data curation, Writing – original draft, Visualization, Investigation.Naoki Matsumura: Methodology, Software, Writing – review & editing.Yuto Iwasaki: Methodology, Software, Writing – review & editing.Yasufumi Sakai: Methodology, Software, Writing – review & editing.Misaho Yamamura: Writing – review & editing.Tomohiko Omura: Writing – review & editing.Junichiro Yamabe: Writing – review & editing.Hisao Matsunaga: Writing – review & editing.K.I.developed the potential, performed and analyzed all simulations, and wrote the paper.N.M., Y.I., and Y.S.developed the software necessary for potential development.M.Y., T.O., J.Y., and H.M.contributed to the discussion regarding comparison with experimental results.All authors discussed the results and commented on the manuscript.

相应的作者

对应Kazuma Ito。

道德声明

竞争利益

作者没有宣称没有竞争利益。

同行评审

同行评审信息

Communications Materialsthanks Edmanuel Torres and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

附加信息

Publisher’s note关于已发表的地图和机构隶属关系中的管辖权主张，Springer自然仍然是中立的。

补充信息

引用本文

Check for updates. Verify currency and authenticity via CrossMark

Ito, K., Matsumura, N., Iwasaki, Y.

等。Predicting hydrogen diffusion in nickel–manganese random alloys using machine learning interatomic potentials.Commun Mater6 , 195 (2025).https://doi.org/10.1038/s43246-025-00924-x

下载引用

  • 已收到：

  • 公认：

  • 出版：

  • doi：https://doi.org/10.1038/s43246-025-00924-x

关于《使用机器学习间电位预测镍 - 山基随机合金中的氢扩散》的评论

暂无评论

发表评论



摘要

*通信材料 *的本文讨论了机器学习的原子间潜能来预测镍曼加尼斯随机合金（NI-MN）中的氢扩散。以下是本文的摘要和要点：＃＃＃ 概括：作者开发了一种机器学习的原子间潜力，以预测Ni-MN随机合金中的氢扩散。他们利用这种潜力模拟氢扩散行为，将其结果与实验数据进行了比较。该研究旨在了解氢如何在复杂合金系统中扩散与氢和工业应用相关的氢。###关键点：1。** ML潜力的发展：** - 机器学习的原子间潜力是专门针对Ni-MN随机合金开发的。 - 这种潜力允许精确模拟原子相互作用，包括涉及氢原子的相互作用。2。**仿真方法：** - 进行分子动力学（MD）模拟，以研究Ni-MN合金中氢的扩散行为。 - Ni和Mn原子的各种浓度和构型被认为了解它们对氢迁移率的影响。3。**与实验的比较：** - 将氢扩散系数的模拟结果与文献的实验数据进行了比较。 - 发现了良好的协议，验证了ML电位的准确性。4。**合金元素的影响：** - 该研究揭示了Ni和MN的不同浓度和排列如何影响合金基质中的氢迁移率。 - 鉴定出氢捕获和扩散位点的特定机制。5。**对工业应用的影响：** - 了解Ni-MN合金中的氢扩散对于设计具有改善工业应用中氢含量的抗性的材料至关重要。 - 这些发现可以告知针对氢储存的新合金或氢相互作用起着关键作用的其他用途的开发。###贡献： - ** Kazuma ITO：**概念化，方法论，软件开发，数据分析，编写原始草案，可视化和调查。 - ** Naoki Matsumura，Yuto Iwasaki，Yasufumi Sakai：**为软件开发和方法学方面做出了贡献。 - ** Misaho Yamamura，Tomohiko Omura，Junichiro Yamabe，Hisao Matsunaga：**提供了相对于实验数据的解释结果的专业知识，并有助于手稿编辑。###道德和致谢：作者没有宣称没有竞争利益。这项研究得到了Riken的HPCI系统研究项目和随附的用户支持计划提供的计算资源的支持。这项工作突出了机器学习潜力在预测复杂扩散行为方面的实用性，提供了对基本科学理解和涉及氢气的实用工业应用具有有价值的见解。

相关新闻

相关讨论