OC
英语轻松读发新版了，欢迎下载、更新

用于预测连续体中绑定状态引起的FANO共振的线形的机器学习方法

2025-08-25 07:38:01 英文原文

作者：Polyutov, S. P.

抽象的

我们认为，对称性受保护的结合状态在介电光栅中具有平面镜像对称性的连续体引起的共振。结果表明，透射率中共振的形状由一个通用公式中的两个参数控制，该参数可以在耦合模式理论的框架中得出。从数值上证明，该公式包含各种线形，包括不对称的Fano，Lorentzian和反Lorentzian共鸣。可以证实，即使在上下对称性的情况下，透射率也始终存在。同时，反射率零通常不存在于单模式近似中。发现可以通过随机森林机器学习方法预测FANO共振的线形，该方法的表现可以超过标准的最小平方方法误差的近似值，而误差的数量级均与训练数据集大小相比。\（n \大约10^4 \）。

别人观看的类似内容

介绍

连续体（BICS）中的光学结合状态是麦克斯韦方程的无源局部解决方案，在光谱中嵌入散射状态的连续体中1，，，，2，，，，3，，，，4，，，，5。介电元面的光学BIC最近已成为用于增强光 - 物质相互作用的重要工具，用于吸收谐振光6，，，，7，，，，8，，，，9，，，，10，感应11，，，，12，谐波产生13，，，，14，，，，15，，，，16和激光17，，，，18，，，，19，，，，20。尽管BICS不与入射光耦合，但在某些控制参数的变化下破坏了系统的对称性21，，，，22导致所谓的准基本数，即长寿命的共振模式，质量因子在参数空间中的BIC方法上差异为无穷大。这种差异在透射频谱中可见，作为崩溃的Fano共振23，，，，24，，，，25，，，，26，，，，27，，，，28并同时导致宿主跨表面的电磁场增强29，，，，30。这张图片在纳米光子学上是通用的31，，，，32，，，，33，，，，34。如图所示35在单个谐振耦合模式近似中，FANO谐振可以描述为两种光学途径之间干扰的产物，即由于谐振模式的激发以及由于频率无关的背景而引起的直接或非谐振途径引起的谐振途径。

在这项工作中，我们研究了介电光栅中对称性光学BIC引起的FANO共振的线形状。导致BICS转化为准BIC的对称性破坏受到正常角度的小偏差的控制。我们的目标是分析可能的共振线形状，并找出可以使用几何和光学特性作为输入参数来预测线形的天气。我们描述FANO共振线形状的工具是时间耦合模式理论（TCMT）35。如今，TCMT被公认为是描述各种光子设备光谱的有效工具36，，，，37，，，，38，，，，39，，，，40，，，，41，，，，42，，，，43由于普遍性和所提供的清晰的物理图片。值得一提的是，我们将在没有上下对称性的情况下考虑光学系统，这可能会影响Fano共振的线形38，，，，44，，，，45，，，，46，，，，47，，，，48。产生元时间上的BIC和准BIC的光学和几何参数通常通过数值求解Maxwell的方程来确定。但是，非常需要预测光学特性，以避免在每个可能的参数集中避免计算昂贵的部分微分方程解决方案。取而代之的是，基于现有数据的插值技术可以提供更有效的替代方案。如今，机器学习技术已经应用于纳米素的各种问题49，，，，50，，，，51，，，，52，，，，53，，，，54，，，，55包括与光学BIC有关的问题56，，，，57，，，，58，，，，59。最近，TCMT方法已与神经网络杂交41，，，，60，，，，61用于光子设备中的共振响应合成。在这里，我们遵循我们以前的工作62我们表明，随机森林机器学习方法能够预测对称介电元面积中光学BIC的频率。我们专注于构造为介电光栅的元浮标上的bics63，，，，64，由于它们在强耦合中的应用，最近引起了极大的关注65，传感器66，，，，67，，，，68，，，，69，折射率70和吸收增强71。在接下来的内容中，我们重新访问了由对称性保护的BIC引起的FANO共振的TCMT，并将随机森林方法与TCMT结合使用，以适应线形预测问题。

TCMT方程

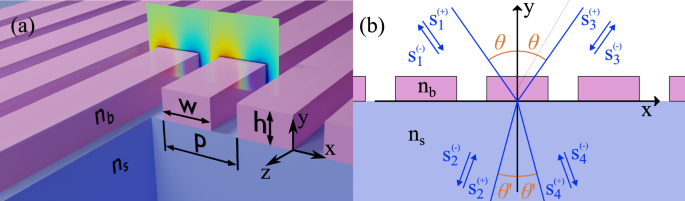
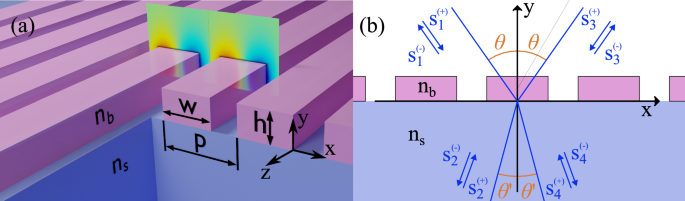
如图所示 1A受审查的系统是由带有折射率的介电条制成的统治光栅\（n_b \）。光栅放在带有折射率的介电底物的顶部\（n_s \）。系统的辅音是空气\（n_0 = 1 \）。所有几何参数，包括周期p，宽度w和高度h在图中指定 1一个。在接下来我们采取的措施中\（p = 0.697〜 \ upmu \ text {m} \）。在所考虑的系统中，波长，线宽和所有几何参数与周期成比例p。结果，这些发现仍然适用于不同时期的晶格。在这项工作中，我们仅考虑沿着沿x - 轴但不沿条形，因此可以在2D电动力学的框架中解决散射问题。图。 1a以z - 电场的组成部分。

图1
figure 1

在介电底物上以介电光栅的形式进行元表面。（（一个）跨表面的示意图，具有反对称BIC模式的电场。（（b）散射通道的定义。

可以在图中看到 1b，散射问题由A描述\（4 \ times 4 \）散射矩阵\（\ wideHat {s} _ {{4}} \）\），将事件的向量和外向振幅链接如下

$$ \ begin {Aligned} \ Mathbf {s} _ {（ - ）} = \ wideHat {s} _ {{4}} \ Mathbf {s} _ {s} _ {（+）}，

（1）

外向\（\ Mathbf {s}^{（ - ）} \）和事件\（\ Mathbf {s}^{（+）} \）向量由

$$ \ begin {Aligned} \ MathBf {s} _ {{（\ pm）}} = \ left（\ begin {array} {c} {c} s_1^{（\ pm）}}}}}}} \ \ s_2^{（s_4^{{（\ pm）}}} \ end {array} \ right）。\ end {Aligned} $$

（2）

我们假设所有电介质都是无损的，所以s-matrix是统一的\（\（\ wideHat {s} _ {{4}}}^{\ dagger} \ wideHat {s} _ {{4}} = \ wideHat {{\ MathBb {i}}}}}}} \）。该系统还具有时间反转对称性s-matrix是对称的\（\ wideHat {s} _ {{4}}}^{\ intercal} = \ wideHat {s} _ {{4}}} \）。重要的是矩阵\（\ wideHat {s} _ {{（4）}} \）\）必须是块形式

$$ \ begin {Aligned} \ wideHat {s} _ {{4}}} = \ left（\ begin {arnay} {cc} {cc} 0＆\ wideHat {s} _ {{2}} {2}}} \ \ \\\\\\\\\\\\\\\\\\\\\\ \\ \ \ \ \ \ \\\ end {array} \ right）\ end {aligned} $$

（3）

为了确保从跨表面散射中的动量保护38， 在哪里\（\ wideHat {s} _ {{2}}} \）是一个\（2 \ times 2 \）统一矩阵。由于系统具有\（\ sigma _v \）镜像对称性问题可以减少到查找\（\ wideHat {s} _2 \）如补充文件所示，这是一个对称矩阵 1。没有失去普遍性的损失，我们可以专注于左波浪，以便

$$ \ begin {aligned} \ left（\ begin {arnay} {c} s_ {1}^{（ - ）} \\ s_ {2}^{（ - ）} \\ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \ right）s_ {3}^{（+）} \\ s_ {4}^{（+）} \\ \\ end {array} \ right）。\ end {Aligned} $$

（4）

根据35描述单模散射的TCMT方程采用以下形式

$$ \ begin {aligned}＆\ frac {d a（t）} {d t} = - （i \ omega _0+\ gamma）a（t）+{\ varvec {\ varvec {\ kappa}}}}\\\ \ \ \ \ \ \ m {s}^{（ - ）}（t）= \ wideHat {c} \ Mathbf {s}^{（+）}（+）}（t）+ a（t）\ a（t）\ mathbf {d}

（5）

在哪里\（\ wideHat {c} \）是直接（非共振）过程的矩阵，\（\ Omega _0 \）是共振中心频率，\（\ gamma \）是辐射衰减率，一个（（t） - 谐振本征的幅度，\（{\ varvec {\ kappa}} \）\）是耦合向量和\（\ Mathbf {D} \）是脱钩向量。在接下来的内容中，我们假设系统是由单色波照明的\（\ omega \），因此等式中所有时间依赖的数量（5）随着谐波因子的及时振荡\（e^{ - i \ omega t} \）。重要的是，TCMT方程中的参数不是独立的，而是由于能源保护，洛伦兹互惠和时间反向对称性所施加的限制而彼此相关的35，，，，72。正如我们已经提到的那样，能量保护在S-矩阵的单位性中表现出来，而时间反转对称性则迫使S-矩阵是对称的。在这种情况下，已知TCMT方程的参数满足以下三个方程35

$$ \ begin {Aligned}＆2 \ gamma = \ Mathbf {d}^{\ dagger} \ Mathbf {d}，\ nonumber \\＆{\ varvec {\ varvec {\ kappa}}\ Mathbf {d}^{*}+\ Mathbf {d} = 0。\ end {Aligned} $$

（6）

在我们的情况下，可以保存节能和时间逆转，但是，在应用时间逆转操作时需要注意，因为它将剩余的波映射到右侧的波浪上。在补充文件中 2我们证明了\（2 \ times 2 \）统一和对称性\（\ wideHat {s} _2 \）导致耦合参数的约束与等式相同的约束（6）。

现在我们必须解决等式（6）用于脱钩矢量。我们从最通用的形式出发\（\ wideHat {c} \），这是统一和对称的，

$ \ begin {Aligned} \ wideHat {c} = e^{i \ phi} \ left（\ begin {array} {cc} {cc} \ rho e^{ - i \ eta}＆i \ e \ i \ tau \\ tau \\ \ \ \ \ \ i \ tau＆\ rho＆\ rho＆\ rho e^e^i \ eta \ e}\ rho = \ sqrt {1- \ tau ^2} \ end {aligned} $$

（7）

和\（\ tau \ in [-1，〜1] \），所有参数均为真实价值。参数\（\ rho \）和\（\ tau \）在等式中（7）分别是反射和传输幅度的绝对值，而\（\ phi，\ eta \ in [0，\ pi] \）描述散射波的相。等式中的参数数量（7）可以通过通过统一转换重新定义事件通道来减少）

$$ \ begin {Aligned} \ left（\ begin {array} {c} {s} {s} _1^{（+）} \\ {s} \\ {s} _2^{（+）} \ end} \ end {array} \ right} \ right）＆e^{i \ phi _2} \ end {array} \ right）\ left（\ begin {arnay} {c} {c} \ tilde {s} _1^{（+）} \ \ \ \ \ \ \ \ \ \ tilde {s} {s}}}} _2^{（+）} {（+）} {（+）} \ end enay}\ end {Aligned} $$

（8）

要与时间反转对称性一致，外向通道必须如下转换

$ \ begin {Aligned} \ left（\ begin {array} {c} {s} {s} _1^{（ - ）} \\ {s} \\ {s} _2^{（ - ）} \ end} \ end {array} \ right} \ right） 0 & e^{-i\phi _2} \end{array} \right) \left( \begin{array}{c} \tilde{s}_1^{ (-)} \\ \tilde{s}_2^{ (-)} \end{array} \right) .\ end {Aligned} $$

（9）

然后，通过使用eq。（8） 和 （9）与等式一起7）一个人到达一个单一对称矩阵的单个参数家族

$ \ begin {Aligned} \ wideHat {c} = \ left（\ begin {array} {cc} \ rho＆i \ tau \ tau \\ i \ tau＆\ tau＆\ rho \ de end {array {array} \ right）[-1，1]，\ end {Aligned} $$

（10）

如果选择

$$ \ begin {aligned} \ phi _1 = \ frac {\ eta - \ phi} {2} {2}，\ \ \ phi _2 = - \ frac {\ eta +\ phi +\ phi} {2

（11）

在等式中（8）。可以轻松地检查上述统一转换符合等式（6）。等式中的统一转型（8）可以将其视为在散射域和沿着外太空之间移动参考平面的y-轴。这总是可以在远场上被散射通道详尽地描述的远场。通过使用等式（10）在等式中（6）找到一个单参数的解决方案家族\（\ Mathbf {D} \）如下

$ \ begin {Aligned} \ begin {Aligned} \ MathBf {d} =＆\ sqrt {\ frac {\ gamma} {（1+\ rho）}}} \ left（\ left（\ left）\\\ \ \ \ tau \ sin \ alpha -i（1+\ rho）\ cos \ alpha \ end {array} \ right），\\ \ alpha \ in＆[ - {\ pi}/{\ pi}/{2}

（12）

派生细节在补充文件中介绍 3。

使用后\（{\ varvec {\ kappa}} = \ mathbf {d} \）在等式中（S10）找到了s-矩阵$$ \ begin {Aligned} \ wideHat {s} = \ wideHat {c}+\ frac {\ MathBf {d} \ Mathbf {d}^{d}^{\ InterCal}}}}}} {i（\ omega _0-- \ omega）+\ omega）+\ gamma}。

\ end {Aligned} $$

（13）

独立于入射方向的传输系数将

$ \ begin {aLigned} t = \ frac {[\ tau（\ omega _0-- \ omega）+ \ rho \ gamma \ sin（2 \ alpha）]^2} {（\ \ omega _0- \ omega _0- \ omega）\ end {Aligned} $$

（14）

如果\（\ alpha = \ pm \ pi /4 \）等式（（14）限制了在35用于具有上向对称性的系统。透射频谱等式（14）符合较早的结果46在不对称单模光学谐振器中衰减速率的基本界限上，在其中表明，透射率仅在对称谐振器中与峰达到峰值。等式（14）不仅可以应用于介电元面上的TM模型。鉴于有一个孤立的共振耦合到两个散射通道，它对任何光学材料仍然有效。

该系统支持对称性受保护的BIC\（\ gamma \）-观点。与入射角的变化\（\ theta \）在\（\ gamma \） - 点BIC转换为高问具有共振频率的谐振模式\（\ Omega _0 \）和衰减率\（\ gamma \）由以下泰勒扩展给出

$$\begin{aligned}&\omega _0=\omega _{ \textrm{BIC}}+\kappa _{\omega }\theta ^2+{\mathscr {O}}(\theta ^4), \nonumber \\&\gamma =\kappa_ {\ gamma} \ theta ^2+\ Mathscr {o}（\ theta ^4）。\ end {Aligned} $$

（15）

使用泰勒膨胀等式（15）在等式中（14）一个到达

$ \ begin {aligned} t = \ frac {[\ tau（\ omega _ {{{\ textrm {bic}}}}}}+ \ omega _0 ^{{（2）}}} \ theta} \ theta ^2- \ omega）（2 \ alpha）\ theta ^2] ^2} {（\ omega _ {{\ textrm {\ textrm {bic}}}}}+\ omega _0 ^{{（2）}}}}}}} \ theta ^2- ^2- \ omega ^2- \ omega ^2+（之间

（16）

这给出了由对称性受保护的BIC引起的FANO共振的线形。

数据集采集

我们的目标是预测图2所示的系统中BIC诱导的FANO共振的形状。 1。根据等式（14），除了共振中心频率\（\ Omega _0 \）和辐射衰减率\（\ gamma \）这是通过主持BIC的泄漏带的分散来指定的，只有两个参数表征了Fano共振的形状，即\（\阿尔法\）和\（\ tau \）。可以通过将数值计算的透射光谱拟合到与正常略有不同的入射角来找到这两个参数。在这项工作中，我们接受\（\ theta = 2 \ \ textrm {deg} \）。相应地，辐射衰减速率和中心频率决定了Fano共振的位置和宽度。因此，为了预测共振的形状，我们必须分析四个参数的方式\（n_b，〜n_s，〜h \）和w影响数量\（\阿尔法\）和\（\ tau \）。在这里，我们通过将机器学习算法应用于通过在所有四个控制参数的变化下求解麦克斯韦方程获得的数据集来解决此问题。参数范围如下指定

$$ \ begin {Aligned} n_b \ in [2，5]，\ n_s \ in [1.5，4]，\ h \ in [0.2p，0.8p]，\ w \ in [0.2p，0.8p]。\ end {Aligned} $$

（17）

请注意，在同时更改两者的迹象之后，共振的线形是相同的\（\阿尔法\）和\（\ tau \）。跟随我们以前的工作62我们专注于Wavelengh范围1100 nm。因此，我们为属性参数指定以下范围

$ \ begin {Aligned} \ tau \ in [-1，1]，\ g \ in [0，1]，\ \ \ \ 2000〜 {\ text {nm}}> \ lambda> \ lambda> \ lambda> \ lambda> 1100〜 {\ text {nm}}}

（18）

在哪里\（\ lambda \）是共振的波长\（\ lambda = 2 \ pi c/\ omega _0 \）和

$$ \ begin {Aligned} g = \ sqrt {1- \ tau ^2} \ sin（2 \ alpha）。\ end {Aligned} $$

（19）

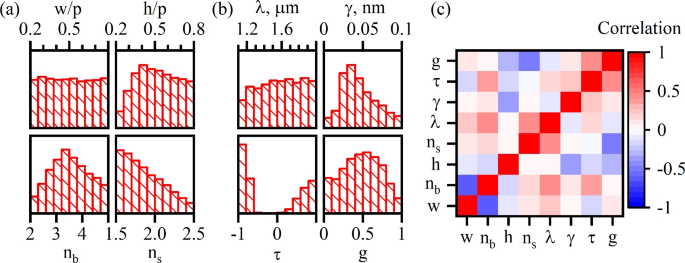
要生成数据集（请参见参考文献。73）我们运行了100,000个数值实验，其中18,836个导致在感兴趣的频率范围内找到对称性的BIC。使用有限元方法（FEM）在COMSOL多物理软件包中使用有限元方法（FEM）进行了模拟。通过等式的最小成方拟合提取了属性参数的计算值。（14）到数值数据。数值实验产生了四个特征参数的值（h，，，，\（n_b \），，，，w，，，，\（n_s \））和四个属性参数（\（\ lambda \），，，，g，，，，\（\ tau \），，，，\（\ gamma \））。在图 2a我们显示了特征参数的分布，而属性参数的分布如图所示。 2b。可以在图中看到 2大多数特征参数和BIC波长（属性）的A，B显示出几乎均匀的分布。这些均匀的分布表明，数据集包含代表性案例。此外，图中所示的相关矩阵 2C证明了功能和属性参数之间没有线性关系，从而证明了机器学习方法的应用。

图2
figure 2

分布（一个）特征参数和（b）计算的属性参数值。（（c）功能和属性参数之间的相关矩阵。随机森林法

为了提高预测属性参数的精度（

\（\ tau \），，，，g，，，，\（\ lambda \），，，，\（\ gamma \）），我们扩展了特征参数的数据集（h，，，，\（n_b \），，，，w，，，，\（n_s \））合并其乘法产品，因此扩展功能数据集还包括（\（H^2 \），，，，\（H \ CDOT N_B \），，，，\（H \ CDOT W \），，，，\（H \ CDOT N_S \），，，，\（n_b^2 \），，，，\（N_B \ CDOT W \），，，，\（n_b \ cdot n_s \），，，，\（w^2 \），，，，\（W \ CDOT N_S \），，，，\（n_s^2 \））。对于预测任务，我们利用了随机森林（RF）算法，这是一种基于回归树的强大集合方法74，，，，75。这种方法涉及通过递归分区多维预测空间来构建多个决策树。在预测阶段，RF模型输出类（用于分类）的模式或从单个树中得出的平均平均预测（回归）76，，，，77。为了实现RF模型，我们使用Python 3.6编程语言开发了一个名为Rancomforest.py的Python脚本78。脚本使用标准库，包括numpy，pandas，sklearn，matplotlib，和mpl_toolkit。为了说明RF算法的随机性质，我们进行了5倍的交叉验证测试，汇总了结果以获得平均性能并计算平均平均误差（MAE）。每次迭代都涉及将数据随机分为两组。一组包括总数据的70％用于训练该模型。其余30％的数据用于测试。结果，我们构建了四个不同的RF模型，一个用于每个属性参数（\（\ tau \），，，，g，，，，\（\ lambda \），，，，\（\ gamma \））。

除了它的预测能力外，RF算法还可以在训练后量化每个特征参数的重要性。这可以通过将所选功能的值在训练数据中置换并计算扰动数据集上的误差来实现。通过平均所有树木置换之前和之后的误差差，以及随后的归一化来获得该特征的重要性评分。79，，，，80。与较低值的特征相比，产生较高值的特征排名更为重要。

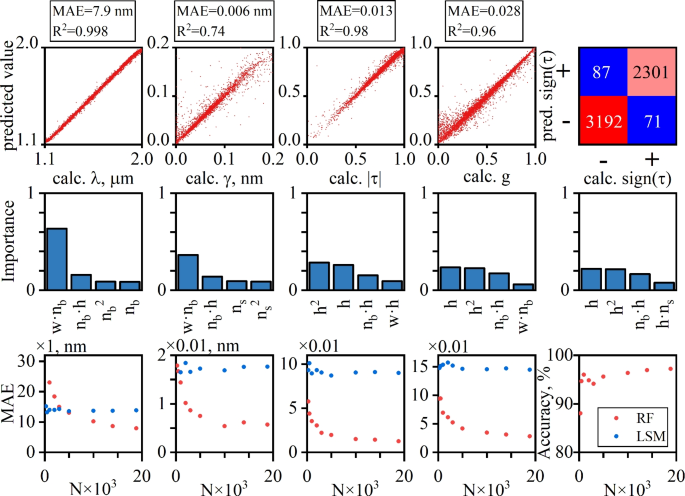
最后，在应用RF方法时，发现该算法无法正确预测属性参数\（\ tau \）当它的绝对价值接近统一时。这是由于等式的结构14），其中分子独立于\（\ tau \）什么时候\（\ rho /\ tau \ ll 1 \）。为了修改这个困难，我们使用了（0,1）的二进制表示\（\ textrm {sign}（\ tau）\）使用分类RF方法进行预测。数量\（| \ tau | \）被用作应用预测RF的属性参数\（\ tau \）。RF算法的应用结果是在图中收集的。 3。在图中 3我们绘制了四个连续属性参数的RF预测与计算值（\（| \ tau | \），，，，g，，，，\（\ lambda \），，，，\（\ gamma \））。这些图由四个最重要特征参数的重要性得分的直方图补充，并通过将RF性能与多项式最小二平方法（LSM）进行比较的图。在二进制参数的情况下，性能由混淆矩阵资格。

图3
figure 3

RF预测四个连续属性参数\（（\ lambda，\ gamma，| \ tau |，g）\）\）和二进制参数\（\ textrm {sign}（\ tau）\）。第一行显示了属性参数的计算出的与预测值。请注意，对于二进制参数\（\ textrm {sign}（\ tau）\）结果以混淆矩阵的形式可视化。第二行显示了扩展特征参数集的四个最大重要性得分的直方图图。第三行将RF方法的性能与LSM进行比较，具体取决于培训数据集的大小n。

结果

我们继续对图中显示的数据进行任何信息。 3。在图的第一行 3我们绘制了来自测试数据集的四个连续属性的计算与RF预测值。第一行中的最后一个图是混乱矩阵\（\ textrm {sign}（\ tau）\）。MAE和确定系数\（r^2 \）对于所有连续属性，均显示在每个图的顶部。可以看到所有属性都可以良好准确，除了\（\ gamma \）。这是由于BIC光谱附近的谐振线宽的奇异行为。也就是说，从那以后\（\ gamma \）它的价值可能会消失很小\（\ theta \）接近正常的发病率，请参见等式（15）。在图的第二行 3我们绘制了预测所有五个属性参数的扩展数据集中四个最重要功能的重要性得分。数据表明，除波长外，该波长主要由横跨杆的光学路径确定62，没有其他属性仅由从扩展特征参数集中的单个参数确定。读者参考参考。62有关预测的更详细的讨论\（\ lambda \）。在图的第三行 3我们将RF与多项式LSM近似的性能进行比较，以依赖于训练数据集的大小。可以看到，对于除谐振波长以外的所有属性，RF都显着优于LSM。而且，对于属性\（| \ tau | \）和g，这仅确定RF的MAE的共振线形状\（\大约\）一个数量级，小于LSM。请注意，二进制属性不可能与最小平方法的比较\（\ Mathrm {{sign}}}（\ tau）\），因此在图中的第三行的最后一块地块中没有显示LSM数据。 3。

收集的数据允许人们对受对称的BIC引起的FANO共振的形状得出一些结论。首先，共振的位置由Wavelengh决定\（\ lambda \）对应于谐振频率\（\ Omega _0 \）。RF方法和LSM可以准确预测此数量，因为这主要由单个特征控制\（W \ CDOT N_B \）。由于BIC的奇异性质，rf方法比通过LSM更好地预测共振的宽度，尽管它是由RF方法预测的。但是，这不会引起困难，因为在任何预制的设置中，谐振宽度很容易受到入射角的控制。最后，共振的线形由\（\ tau \）和\（\阿尔法\），两者均通过RF方法有效预测。值得一提的是，根据图2的数据 2分布\（\ tau \）有以下动量\（\ langle | \ tau | \ rangle = 0.791 \）， 和\（\ langle \ tau ^2 \ rangle = 0.653 \）。这意味着在背景上观察到共振的经常，而透射率主导着反射。分布的前两个矩\（\阿尔法\）如下\（\ langle \ alpha \ rangle = 0.577 \）， 和\（\ langle \ alpha ^2 \ rangle = 0.376 \）。值得注意的是，平均而言\（\阿尔法\）接近\（\ pi /4=0.785 \）对应于具有上向镜子对称性的元时间。正如已经提到的那样，单位传输仅发生在\（\ alpha = \ pi /4 \）。因此，从统计学上讲，观察到的FANO共振可能在Fano共振的峰值处表现出近乎单位的传播。

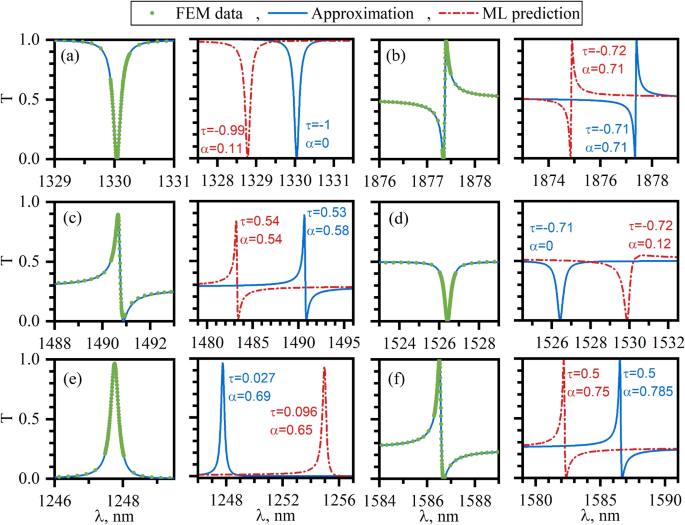
FANO共振的曲线在图中进行了证明。 4我们从测试数据集中绘制六个不同的线形。对于每种情况，首先将FEM数据与等式进行比较。（14）在每个子图的左面板上。在每个子图的右侧面板上，我们证明了RF预测的线形与等式相比（14）。可以看到，在每种情况下，RF预测的共振的位置都会相对于计算出的距离通过更大的距离的距离。这是由于平均质量因子的共鸣消失了很小的线路。\（q = 8166 \）在整个数据集的BIC的光谱附近。请注意，尽管根据图 3谐振波长被预测为良好的精度，RF无法正确地将共振定位在其线路宽度的尺度上。相反，RF预测共振的线形非常适合计算出的数据。请注意，在系统的审查中，包括不对称的Fano图。 4B，C，F，Lorentzian图 4E和反Lorentzian图。 4A，D线形状。请注意，在图2中显然不存在数值精确的反射率零，在共振的倾角下始终达到零。4光盘。最后，我们注意到，在正常发病率的方法中，FANO共振崩溃了，并且透射率变得独立于频率\（t = \ tau ^2 \）。

图4
figure 4

介电光栅中对称性受保护的BIC引起的FANO共鸣。FEM计算数据绿色圆圈，等式的数据近似（14） - 实心蓝线，测试数据集Dash点红线中的RF预测。获得的数值和RF预测值\（\阿尔法\）和\（\ tau \）在每个子图中显示。

讨论

在这项工作中，我们调查了介电光栅中连续体中对称性受保护状态引起的FANO共振的线形。从数值上证明，线形由等式中的两个参数控制（14）包括各种线形，包括不对称的Fano，Lorentzian和Anti-Lorentzian共鸣。完全根据以前的研究46，，，，48，，，，81可以证实，即使在上下对称性的情况下，透射率也始终存在。同时，只有在参数时才能意外接触反射率零\（\阿尔法\）在等式中（14）接近\（\ pi /4 \）。发现可以通过随机森林机器学习方法预测FANO共振的线形，以良好的准确性，该方法在训练数据集尺寸的情况下通过误差的标准最小平方方法近似均优于标准的最小平方方法近似\（n \大约10^4 \）。我们推测，所提出的结果可能对具有一维周期性的全型元时间的设计和综合对谐振响应的设计和合成很有用。对于具有二维周期性图案的元时间，我们的方法将需要概括以说明极化串扰。这代表了未来研究的有趣方向。

数据可用性

支持本研究结果和Python脚本的数据可在Gitlab上获得：https://gitlab.com/nanoworld_ml/bic-ml。参考

Hsu, C. W., Zhen, B., Stone, A. D., Joannopoulos, J. D. & Soljačić, M. Bound states in the continuum.

  1. 纳特。牧师。 1, 16048.https://doi.org/10.1038/natrevmats.2016.48（2016）。

    文章一个 广告一个 Google Scholar一个 

  2. Koshelev, K., Bogdanov, A. & Kivshar, Y. Meta-optics and bound states in the continuum.科学。公牛。 64, 836–842 (2019).

    Google Scholar一个 

  3. Koshelev, K., Favraud, G., Bogdanov, A., Kivshar, Y. & Fratalocchi, A. Nonradiating photonics with resonant dielectric nanostructures.纳米原理 8, 725–745.https://doi.org/10.1515/nanoph-2019-0024（2019）。

    文章一个 Google Scholar一个 

  4. Joseph, S., Pandey, S., Sarkar, S. & Joseph, J. Bound states in the continuum in resonant nanostructures: An overview of engineered materials for tailored applications.纳米原理 10, 4175–4207 (2021).

    Google Scholar一个 

  5. Kang, M., Liu, T., Chan, C. T. & Xiao, M. Applications of bound states in the continuum in photonics.纳特。Rev. Phys。 5, 659–678.https://doi.org/10.1038/s42254-023-00642-8（2023）。

    文章一个 Google Scholar一个 

  6. Zhang, M. & Zhang, X. Ultrasensitive optical absorption in graphene based on bound states in the continuum.科学。代表。 5, 1–6 (2015).

    MathScinet一个 Google Scholar一个 

  7. Wang，X。等。Controlling light absorption of graphene at critical coupling through magnetic dipole quasi-bound states in the continuum resonance.物理。Rev. B 102, 155432 (2020).

    广告一个 Google Scholar一个 

  8. Sang, T., Dereshgi, S. A., Hadibrata, W., Tanriover, I. & Aydin, K. Highly efficient light absorption of monolayer graphene by quasi-bound state in the continuum.纳米材料 11, 484 (2021).

    PubMed一个 PubMed Central一个 Google Scholar一个 

  9. Xiao, S., Wang, X., Duan, J., Liu, T. & Yu, T. Engineering light absorption at critical coupling via bound states in the continuum.JOSA B 38, 1325–1330 (2021).

    广告一个 Google Scholar一个 

  10. Cai, Y., Liu, X., Zhu, K., Wu, H. & Huang, Y. Enhancing light absorption of graphene with dual quasi bound states in the continuum resonances.J. Quant.光谱。Radiat.Transf. 283, 108150 (2022).

    Google Scholar一个 

  11. Liu, Y., Zhou, W. & Sun, Y. Optical refractive index sensing based on high-Q bound states in the continuum in free-space coupled photonic crystal slabs.Sensors 17, 1861.https://doi.org/10.3390/s17081861（2017）。

    文章一个 广告一个 PubMed一个 PubMed Central一个 Google Scholar一个 

  12. Romano, S. et al.Label-free sensing of ultralow-weight molecules with all-dielectric metasurfaces supporting bound states in the continuum.Photonics Res. 6, 726.https://doi.org/10.1364/prj.6.000726（2018）。

    文章一个 Google Scholar一个 

  13. Ndangali, F. R. & Shabanov, S. V. The resonant nonlinear scattering theory with bound states in the radiation continuum and the second harmonic generation.在Active Photonic Materials V, vol.8808, 88081F (International Society for Optics and Photonics, 2013).

  14. Wang, T. & Zhang, S. Large enhancement of second harmonic generation from transition-metal dichalcogenide monolayer on grating near bound states in the continuum.选择。表达 26, 322–337 (2018).

    广告一个 PubMed一个 Google Scholar一个 

  15. Carletti, L., Koshelev, K., De Angelis, C. & Kivshar, Y. Giant nonlinear response at the nanoscale driven by bound states in the continuum.物理。莱特牧师。 121, 033903 (2018).

    广告一个 PubMed一个 Google Scholar一个 

  16. Koshelev, K. et al.Subwavelength dielectric resonators for nonlinear nanophotonics.科学 367, 288–292 (2020).

    广告一个 PubMed一个 Google Scholar一个 

  17. Kodigala, A. et al.Lasing action from photonic bound states in continuum.自然 541, 196–199.https://doi.org/10.1038/nature20799（2017）。

    文章一个 广告一个 PubMed一个 Google Scholar一个 

  18. Hwang, M.-S.等。Ultralow-threshold laser using super-bound states in the continuum.纳特。社区。 12, 4135.https://doi.org/10.1038/s41467-021-24502-0（2021）。

    文章一个 广告一个 PubMed一个 PubMed Central一个 Google Scholar一个 

  19. Yu, Y. et al.Ultra-coherent fano laser based on a bound state in the continuum.纳特。光子学 15, 758–764.https://doi.org/10.1038/s41566-021-00860-5（2021）。

    文章一个 广告一个 Google Scholar一个 

  20. Yang, J.-H.等。Low-threshold bound state in the continuum lasers in hybrid lattice resonance metasurfaces.激光光子学修订版。 15, 2100118 (2021).

    广告一个 Google Scholar一个 

  21. Koshelev, K., Lepeshov, S., Liu, M., Bogdanov, A. & Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum.物理。莱特牧师。 121, 193903.https://doi.org/10.1103/physrevlett.121.193903（2018）。

    文章一个 广告一个 PubMed一个 Google Scholar一个 

  22. Maksimov, D. N., Gerasimov, V. S., Romano, S. & Polyutov, S. P. Refractive index sensing with optical bound states in the continuum.选择。表达 28, 38907.https://doi.org/10.1364/oe.411749（2020）。

    文章一个 广告一个 PubMed一个 Google Scholar一个 

  23. Shipman, S. P. & Venakides, S. Resonant transmission near nonrobust periodic slab modes.物理。Rev. E 71, 026611 (2005).

    广告一个 Google Scholar一个 

  24. Sadreev, A. F., Bulgakov, E. N. & Rotter, I. Bound states in the continuum in open quantum billiards with a variable shape.物理。Rev. B 73, 235342 (2006).

    广告一个 Google Scholar一个 

  25. Blanchard, C., Hugonin, J.-P.& Sauvan, C. Fano resonances in photonic crystal slabs near optical bound states in the continuum.物理。Rev. B 94, 155303.https://doi.org/10.1103/physrevb.94.155303（2016）。

    文章一个 广告一个 Google Scholar一个 

  26. Bogdanov, A. A. et al.Bound states in the continuum and fano resonances in the strong mode coupling regime.ADV。光子学 1, 016001 (2019).

    广告一个 Google Scholar一个 

  27. Pankin, P. S., Maksimov, D. N., Chen, K.-P.& Timofeev, I. V. Fano feature induced by a bound state in the continuum via resonant state expansion.科学。代表。 10, 13691.https://doi.org/10.1038/s41598-020-70654-2（2020）。

    文章一个 PubMed一个 PubMed Central一个 Google Scholar一个 

  28. Bulgakov, E. N. & Maksimov, D. N. Optical response induced by bound states in the continuum in arrays of dielectric spheres.J. Opt.Soc。是。b 35, 2443.https://doi.org/10.1364/josab.35.002443（2018）。

    文章一个 广告一个 Google Scholar一个 

  29. Yoon, J. W., Song, S. H. & Magnusson, R. Critical field enhancement of asymptotic optical bound states in the continuum.科学。代表。 5, 18301.https://doi.org/10.1038/srep18301（2015）。

    文章一个 广告一个 PubMed一个 PubMed Central一个 Google Scholar一个 

  30. Mocella, V. & Romano, S. Giant field enhancement in photonic resonant lattices.物理。Rev. B 92, 155117.https://doi.org/10.1103/physrevb.92.155117（2015）。

    文章一个 广告一个 Google Scholar一个 

  31. Campione, S. et al.Broken symmetry dielectric resonators for high quality factor fano metasurfaces.ACS光子学 3, 2362–2367.https://doi.org/10.1021/acsphotonics.6b00556（2016）。

    文章一个 Google Scholar一个 

  32. Zhou，W。等。Progress in 2d photonic crystal fano resonance photonics.prog。量子电子。 38, 1–74 (2014).

    广告一个 Google Scholar一个 

  33. Limonov, M. F., Rybin, M. V., Poddubny, A. N. & Kivshar, Y. S. Fano resonances in photonics.纳特。光子学 11, 543–554.https://doi.org/10.1038/nphoton.2017.142（2017）。

    文章一个 Google Scholar一个 

  34. Krasnok, A. et al.Anomalies in light scattering.ADV。选择。光子学 11, 892.https://doi.org/10.1364/aop.11.000892（2019）。

    文章一个 广告一个 Google Scholar一个 

  35. Fan, S., Suh, W. & Joannopoulos, J. D. Temporal coupled-mode theory for the fano resonance in optical resonators.J. Opt.Soc。是。一个 20, 569.https://doi.org/10.1364/josaa.20.000569（2003）。

    文章一个 广告一个 Google Scholar一个 

  36. Alpeggiani, F., Parappurath, N., Verhagen, E. & Kuipers, L. Quasinormal-mode expansion of the scattering matrix.物理。Rev. X 7, 021035.https://doi.org/10.1103/PhysRevX.7.021035（2017）。

    文章一个 Google Scholar一个 

  37. Ming, X., Liu, X., Sun, L. & Padilla, W. J. Degenerate critical coupling in all-dielectric metasurface absorbers.选择。表达 25, 24658.https://doi.org/10.1364/oe.25.024658（2017）。

    文章一个 广告一个 PubMed一个 Google Scholar一个 

  38. Zhou, H. et al.Perfect single-sided radiation and absorption without mirrors.Optica 3, 1079.https://doi.org/10.1364/optica.3.001079（2016）。

    文章一个 广告一个 Google Scholar一个 

  39. Maksimov, D. N., Bogdanov, A. A. & Bulgakov, E. N. Optical bistability with bound states in the continuum in dielectric gratings.物理。Rev. A 102, 033511 (2020).

    广告一个 Google Scholar一个 

  40. Bikbaev, R. G., Maksimov, D. N., Pankin, P. S., Chen, K.-P.& Timofeev, I. V. Critical coupling vortex with grating-induced high q-factor optical tamm states.选择。表达 29, 4672.https://doi.org/10.1364/oe.416132（2021）。

    文章一个 广告一个 PubMed一个 Google Scholar一个 

  41. Zhang, J. et al.Physics-driven machine-learning approach incorporating temporal coupled mode theory for intelligent design of metasurfaces.IEEE Trans。Microw.Theory Tech. 71, 2875–2887.https://doi.org/10.1109/tmtt.2023.3238076（2023）。

    文章一个 广告一个 Google Scholar一个 

  42. Wu, H., Yuan, L. & Lu, Y. Y. Approximating transmission and reflection spectra near isolated nondegenerate resonances.物理。Rev. A 105, 063510.https://doi.org/10.1103/physreva.105.063510（2022）。

    文章一个 广告一个 MathScinet一个 Google Scholar一个 

  43. Huang, Z., Wang, J., Jia, W., Zhang, S. & Zhou, C. All-dielectric metasurfaces enabled by quasi-bic for high-q near-perfect light absorption.选择。Lett。 50, 105.https://doi.org/10.1364/ol.541553（2024）。

    文章一个 Google Scholar一个 

  44. Popov, E., Mashev, L. & Maystre, D. Theoretical study of the anomalies of coated dielectric gratings.选择。Acta Int.J. Opt. 33, 607–619.https://doi.org/10.1080/713821994（1986）。

    文章一个 广告一个 Google Scholar一个 

  45. Shipman, S. P. & Tu, H. Total resonant transmission and reflection by periodic structures.Siam J. Appl。数学。 72, 216–239.https://doi.org/10.1137/110834196（2012年）。

    文章一个 MathScinet一个 Google Scholar一个 

  46. Wang, K. X., Yu, Z., Sandhu, S. & Fan, S. Fundamental bounds on decay rates in asymmetric single-mode optical resonators.选择。Lett。 38, 100.https://doi.org/10.1364/ol.38.000100（2013）。

    文章一个 广告一个 PubMed一个 Google Scholar一个 

  47. Bykov, D. A. & Doskolovich, L. L.\(\omega -k_x\)Fano line shape in photonic crystal slabs.物理。Rev. A 92, 013845.https://doi.org/10.1103/physreva.92.013845（2015）。

    文章一个 广告一个 Google Scholar一个 

  48. Yuan, L., Zhang, M. & Lu, Y. Y. Real transmission and reflection zeros of periodic structures with a bound state in the continuum.物理。Rev. A 106, 013505.https://doi.org/10.1103/physreva.106.013505（2022）。

    文章一个 广告一个 MathScinet一个 Google Scholar一个 

  49. Ma, W. et al.Deep learning for the design of photonic structures.纳特。光子学 15, 77–90 (2021).

    广告一个 Google Scholar一个 

  50. Jiang, J., Chen, M. & Fan, J. A. Deep neural networks for the evaluation and design of photonic devices.纳特。牧师。 6, 679–700 (2021).

    广告一个 Google Scholar一个 

  51. So, S., Badloe, T., Noh, J., Bravo-Abad, J. & Rho, J. Deep learning enabled inverse design in nanophotonics.纳米原理 9, 1041–1057 (2020).

    Google Scholar一个 

  52. Pilozzi, L., Farrelly, F. A., Marcucci, G. & Conti, C. Machine learning inverse problem for topological photonics.社区。物理。 1, 57 (2018).

    Google Scholar一个 

  53. Kudyshev, Z. A., Shalaev, V. M. & Boltasseva, A. Machine learning for integrated quantum photonics.ACS光子学 8, 34–46 (2020).

    Google Scholar一个 

  54. Zhao, Z. et al.Advancements in microwave absorption motivated by interdisciplinary research.ADV。母校。 36。https://doi.org/10.1002/adma.202304182（2023）。

  55. Deng, Y., Fan, K., Jin, B., Malof, J. & Padilla, W. J. Physics-informed learning in artificial electromagnetic materials.Appl.物理。Rev. 12。https://doi.org/10.1063/5.0232675（2025）。

  56. Lin, R., Alnakhli, Z. & Li, X. Engineering of multiple bound states in the continuum by latent representation of freeform structures.Photonics Res. 9, B96–B103 (2021).

    Google Scholar一个 

  57. Ma, X. et al.Strategical deep learning for photonic bound states in the continuum.激光光子学修订版。 16, 2100658 (2022).

    广告一个 Google Scholar一个 

  58. Wang, F. et al.Automatic optimization of miniaturized bound states in the continuum cavity.选择。表达 31, 12384–12396 (2023).

    广告一个 PubMed一个 Google Scholar一个 

  59. Wang, Z. et al.Customizing 2.5d out-of-plane architectures for robust plasmonic bound-states-in-the-continuum metasurfaces.ADV。科学。 10, 2206236.https://doi.org/10.1002/advs.202206236（2023）。

    文章一个 Google Scholar一个 

  60. Zhang, Y. et al.Dynamics of polarization-tuned mirror symmetry breaking in a rotationally symmetric system.纳特。社区。 15, 5586.https://doi.org/10.1038/s41467-024-49696-x（2024）。

    文章一个 PubMed一个 PubMed Central一个 Google Scholar一个 

  61. Su, J. L. et al.Metaphynet: intelligent design of large-scale metasurfaces based on physics-driven neural network.J. Phys。光子学 6, 035010.https://doi.org/10.1088/2515-7647/ad4cc8（2024）。

    文章一个 广告一个 Google Scholar一个 

  62. Molokeev, M. S. et al.Infrared bound states in the continuum: random forest method.选择。Lett。 48, 4460.https://doi.org/10.1364/ol.494629（2023）。

    文章一个 广告一个 PubMed一个 Google Scholar一个 

  63. Bulgakov, E. N., Maksimov, D. N., Semina, P. N. & Skorobogatov, S. A. Propagating bound states in the continuum in dielectric gratings.J. Opt.Soc。是。b 35, 1218–1222.https://doi.org/10.1364/josab.35.001218（2018）。

    文章一个 广告一个 Google Scholar一个 

  64. Zhong, H., He, T., Meng, Y. & Xiao, Q. Photonic bound states in the continuum in nanostructures.材料 16, 7112 (2023).

    广告一个 PubMed一个 PubMed Central一个 Google Scholar一个 

  65. Son, H. et al.Strong coupling induced bound states in the continuum in a hybrid metal-dielectric bilayer nanograting resonator.ACS光子学 11, 3221–3231 (2024).

    Google Scholar一个 

  66. Maksimov, D. N., Gerasimov, V. S., Bogdanov, A. A. & Polyutov, S. P. Enhanced sensitivity of an all-dielectric refractive index sensor with an optical bound state in the continuum.物理。Rev. A 105, 033518 (2022).

    广告一个 MathScinet一个 Google Scholar一个 

  67. Wu, W., Wang, K. & Qian, L. All-dielectric grating-based refractive index sensor with a high figure of merit driven by bound states in the continuum.选择。工程。 63, 127104–127104 (2024).

    Google Scholar一个 

  68. Li, Z., Nie, G., Chen, Z., Zhan, S. & Lan, L. High-quality quasi-bound state in the continuum enabled single-nanoparticle virus detection.选择。Lett。 49, 3380–3383 (2024).

    广告一个 PubMed一个 Google Scholar一个 

  69. Yao, H.-Y., Kang, Y.-T.& Her, T.-H.Ultra-sensitive refractive index sensing enabled by accidental bound states in the continuum on ultrathin dielectric grating metasurfaces.选择。表达 33, 13298–13315 (2025).

    PubMed一个 Google Scholar一个 

  70. Yadav, G., Sahu, S., Kumar, R. & Jha, R. Bound states in the continuum empower subwavelength gratings for refractometers in visible.在光子学, vol. 9, 292 (MDPI, 2022).

  71. Liu, J. & Liu, Y. Perfect narrow-band absorber of monolayer borophene in all-dielectric grating based on quasi-bound state in the continuum.安。物理。 535, 2200500 (2023).

    Google Scholar一个 

  72. Zhao, Z., Guo, C. & Fan, S. Connection of temporal coupled-mode-theory formalisms for a resonant optical system and its time-reversal conjugate.物理。Rev. A 99, 033839.https://doi.org/10.1103/physreva.99.033839（2019）。

    文章一个 广告一个 Google Scholar一个 

  73. Maksimov, D. et al.Dataset: Regression.https://opticapublishing.figshare.com/s/99bdf72248fca9e967a3。Breiman, L. Random forests.

  74. 马赫。学习。 45, 5–32.https://doi.org/10.1023/A:1010933404324（2001）。

    文章一个 Google Scholar一个 

  75. Ho, T. K. Random decision forests.在Proceedings of 3rd International Conference on Document Analysis and Recognition, vol. 1, 278–282.https://doi.org/10.1109/ICDAR.1995.598994（1995）。

  76. Liu, Y., Wang, Y. & Zhang, J.New Machine Learning Algorithm: Random Forest, 246–252.(Springer, 2012).

  77. Segal, M. R. Machine learning benchmarks and random forest regression.https://escholarship.org/uc/item/35x3v9t4。Van Rossum, G. & Python Dev Team.

  78. Python 3.6 Language Reference(Samurai Media, 2016).Altmann, A., ToloÅŸi, L., Sander, O. & Lengauer, T. Permutation importance: A corrected feature importance measure.

  79. 生物信息学26 , 1340–1347.https://doi.org/10.1093/bioinformatics/btq134（2010）。文章

    一个 PubMed一个 Google Scholar一个 Wehenkel, M., Sutera, A., Bastin, C., Geurts, P. & Phillips, C. Random forests based group importance scores and their statistical interpretation: Application for alzheimer’s disease.正面。

  80. Neurosci。12。 https://doi.org/10.3389/fnins.2018.00411（2018）。Gippius, N. A., Tikhodeev, S. G. & Ishihara, T. Optical properties of photonic crystal slabs with an asymmetrical unit cell.物理。

  81. Rev. B72 , 045138.https://doi.org/10.1103/physrevb.72.045138（2005）。文章

    一个 广告一个 Google Scholar一个 下载参考致谢

This study was supported by the Ministry of Science and Higher Education of Russian Federation (Grant FSRZ-2023-0006), A.S.K.

acknowledges the support by the Foundation for the Advancement of Theoretical Physics and Mathematics “BASIS” (Grant 23-1-5-76-1), M.S.M.

acknowledges the support by the Ministry of Science and Higher Education of Russian Federation (Grant FEWZ-2024-0052), V.S.G.and A.E.E.acknowledges the support by the Ministry of Science and Higher Education of Russian Federation (Grant 124012900550-1).

资金

Open access funding provided by Royal Institute of Technology.

作者信息

作者和隶属关系

  1. International Research Center of Spectroscopy and Quantum Chemistry, Siberian Federal University, Krasnoyarsk, Russia, 660041

    V. S. Gerasimov, A. S. Kostyukov, A. E. Ershov, D. N. Maksimov & S. P. Polyutov

  2. Institute of Computational Modelling SB RAS, Krasnoyarsk, Russia, 660036

    V. S. Gerasimov & A. E. Ershov

  3. Kirensky Institute of Physics, Federal Research Center KSC SB RAS, Krasnoyarsk, Russia, 660036

    D. N. Maksimov & M. S. Molokeev

  4. Theoretical Chemistry and Biology, KTH Royal Institute of Technology, 106 91, Stockholm, Sweden

    V. Kimberg

  5. Laboratory of Theory and Optimization of Chemical and Technological Processes, University of Tyumen, Tyumen, Russia, 625003

    M. S. Molokeev

  6. Federal Siberian Research Clinical Centre under the Federal Medical Biological Agency, Krasnoyarsk, Russia, 660037

    S. P. Polyutov

作者

  1. V. S. Gerasimov
  2. A. S. Kostyukov
  3. A. E. Ershov
  4. D. N. Maksimov
  5. V. Kimberg
  6. M. S. Molokeev
  7. S. P. Polyutov

贡献

Theory: D.N.M.;FEM calculation: V.S.G., A.S.K.;Machine Learning calculation: M.S.M., A.E.E.;Results analysis: V.K., S.P.P.;Manuscript preparation: V.S.G., D.N.M., M.S.M.All authors reviewed the manuscript.

相应的作者

对应V. Kimberg。道德声明

竞争利益

作者没有宣称没有竞争利益。

附加信息

Publisher’s note

关于已发表的地图和机构隶属关系中的管辖权主张，Springer自然仍然是中立的。

补充信息

权利和权限

引用本文

Check for updates. Verify currency and authenticity via CrossMark

Gerasimov, V.S., Kostyukov, A.S., Ershov, A.E.

等。Machine learning method for predicting line-shapes of Fano resonances induced by bound states in the continuum.Sci代表15 , 31187 (2025).https://doi.org/10.1038/s41598-025-16192-1

下载引用

  • 已收到：

  • 公认：

  • 出版：

  • doi：https://doi.org/10.1038/s41598-025-16192-1

关于《用于预测连续体中绑定状态引起的FANO共振的线形的机器学习方法》的评论

暂无评论

发表评论



摘要

纸质“用于预测连续体中结合状态引起的FANO共振的线形的机器学习方法”探索了一种机器学习方法，以预测FANO共振的线形状，这些方法是在连续体（BSC）中具有绑定状态的光学系统中观察到的关键现象。这项研究的主要贡献和发现可以总结如下：###关键贡献1。** ML模型的开发**： - 利用机器学习算法，特别是随机森林，以预测FANO共振的线形状。 - 开发了一个数据集，用于基于严格的有限元方法（FEM）计算训练模型。2。**特征重要性分析**： - 采用置换的重要性得分来分析和了解哪些物理参数在塑造FANO共振线形状方面最有影响力。3。**预测准确性**： - 在预测FANO共振的强度曲线和峰位置方面达到了很高的精度，证明了ML方法对复杂的光学系统的有效性。###关键发现1。**参数影响线形状**： - 确定的关键参数，例如光栅周期（音高）和厚度，显着影响FANO共振的线形状。2。**验证和解释**： - 通过与实验数据或更详细的模拟进行比较，验证了机器学习预测，以确保可靠性。3。**应用程序范围**： - 在光学传感中证明了潜在的应用，其中精确控制BSC诱导的FANO共振可以增强灵敏度和检测能力。###方法论1。** FEM计算**： - 使用有限元方法计算来生成用于各种配置的线形的综合数据集。2。**随机森林算法**： - 应用以鲁棒性在处理高维数据集中闻名的随机森林算法来建模和预测FANO共振特性。3。**置换重要性分析**： - 采用置换重要性分析来解释功能相关性并提高模型透明度。###含义1。**光学传感**： - 结果突出了BSC诱导的FANO共振对高度敏感的折射率传感的潜力，这些折射率感测在化学检测和生物传感等各个领域。2。**设计优化**： - 提供了一个预测工具，可以帮助设计具有针对特定应用程序的优化线形的光学系统。3。**理论见解**： - 更深入地了解Fano共振的基本物理学，从而弥合理论理解和实际应用。＃＃＃ 结论这项研究展示了如何有效地使用机器学习技术来预测复杂的现象，例如连续体中结合状态引起的光学系统中的FANO共振。该方法不仅提供了准确的预测，而且还增强了我们对影响这些共振的关键参数的理解，为光学传感及其他方面的更高级和精确的应用铺平了道路。###未来方向1。**进一步的数据集扩展**： - 通过更多的配置和材料属性扩展数据集可以进一步完善预测功能。2。**实时传感应用程序**： - 开发动态光学系统的实时预测模型可以增强快速检测和监视应用程序。3。**其他技术的集成**： - 探索与其他计算方法（例如神经网络）的集成，以达到更高的准确性或解释能力。通过利用机器学习，这项工作为光学物理和相关技术领域的理论探索和实际实现开辟了新的途径。

相关新闻

相关讨论