Machine learning augmented design of 2D magnet with planar cyclo-tetranitrogen: ambient thermal stability from quantum to mesoscale
作者:Lyu, Pengbo
Polynitrogen compounds have emerged as a compelling frontier in materials science due to their extraordinary energy densities and novel bonding motifs1,2. In nitrogen-rich systems, conversion of single- or double-bonded N–N units to the N ≡ N triple bond of N2 is highly exothermic3. As a result, any extended network of nitrogen atoms stores large energy but is intrinsically metastable. Recent breakthroughs have nevertheless expanded the known chemistry of polynitrogen1,4,5. Until very recently, only three “homonuclear” polynitrogen ions were isolable in bulk at ambient conditions, the azide ([N3]−), pentazenium cation ([N5]+), and cyclo-pentazolate anion ([c-N5]−), but high-pressure and coordination-chemistry routes have produced many more1,6,7,8. For example, state-of-the-art high-pressure techniques have enabled the isolation of high-energy species like pentazolates ([N5]−) and the trapping of linear N3 radicals under extreme conditions6,7. High-pressure synthesis has further expanded the repertoire of polynitrogen structures: i.e., a cesium polynitride (CsN5) compound with nitrogen chains was stabilized at 78 GPa9, and GaN5 was shown to host 12-membered nitrogen ring at 80 GPa10. Metal-mediated stabilization strategies have also yielded other metastable nitrogen-rich species, such as Mg2N4 containing syn-N4 anions, the N4 unit remains metastable and requires specific coordination environments to suppress dissociation7,11. Similarly, high-pressure Fe−N compounds (e.g., FeN4, GaN10, and Sc2N8) stabilize polymeric nitrogen chains, but their formation is limited by harsh synthesis conditions9,10,11. Collectively, these high-pressure and coordination-chemistry routes demonstrate that diverse polynitrogen allotropes – from bent N3 and cyclic N₅ units to extended N6 and N8 networks – can be realized.
Despite these advances, ambient stability remains a critical bottleneck for polynitrogen materials. The inherent metastability arises from two key factors. First, odd-membered nitrogen clusters (e.g., N3, N5) contain unpaired electrons that drive rapid radical recombination. Second, even-membered clusters (e.g., N4, N8) suffer significant strain when incorporated into three-dimensional networks, leading to weakened N–N bonds7,11. Consequently, most polynitrogen frameworks require extreme pressures (>10 GPa) or cryogenic confinement (<100 K) to persist, as exemplified by cubic-gauche nitrogen (cg-N) synthesized at 110 GPa and 2000 K12. Upon releasing pressure or warming, most polynitrogen frameworks spontaneously collapse to N2. Therefore, despite their remarkable energy content, polynitrogen clusters remain kinetically labile and have generally been isolated only as salts or within inert matrices. Overcoming these stability challenges is an active area of research, but to date, extreme conditions still impose severe practical limits on using polynitrogen motifs under ambient conditions.
The emergence of two‑dimensional (2D) materials offers a promising alternative for polynitrogen stabilization. Notably, triclinic beryllium tetranitride (BeN4), synthesized under high-pressure conditions, was found to transform into a layered structure with van der Waals interlayer interactions and a low exfoliation energy13. After that, several metal nitride (MN) monolayers, such as NiN214, CrN415, BeN416 etc., have been theoretically/experimentally demonstrated. However, in most of these systems, the N4 motif does not form an inherent ring structure. Instead, prior studies have largely focused on thermodynamically favoured nitrogen-rich phases with N–N single or N = N double bonds, often overlooking the metastable structure with cyclo-N4 units17,18, because they are commonly dismissed as metastable architectures. This bias reflects the widespread assumption that metastability inherently undermines structural integrity and functional applicability. Consequently, the distinct physicochemical properties associated with the unique geometry with cyclo-N4 unit have largely remained unexplored.
Herein, we present the t-FeN4 monolayer as a significant advancement in the stabilisation of ambient polynitrogen through 2D coordination engineering. Unlike previous Fe−N systems synthesized at high pressures11, the t-FeN4 monolayer stabilizes the cyclo-N4 ring at ambient conditions through strong Fe−N coordination, yielding distinctive electronic and magnetic properties. Furthermore, we developed a machine-learning potential (MLP) trained on first-principles datasets for t-FeN4 monolayer, achieving high accuracy across diverse configurations including extended monolayers, nanoribbons, and nanosheets. The MLP’s transferability enables large-scale molecular dynamics simulations (>100,000 atoms and nanosecond time scales), revealing exceptional thermal stability of the t-FeN4 monolayer up to 800 K. Our findings provide convincing evidence that 2D confinement can stabilise exotic cyclo-N4 topology at ambient pressure. This establishes a general strategy for the development of next-generation energy and spintronic materials.
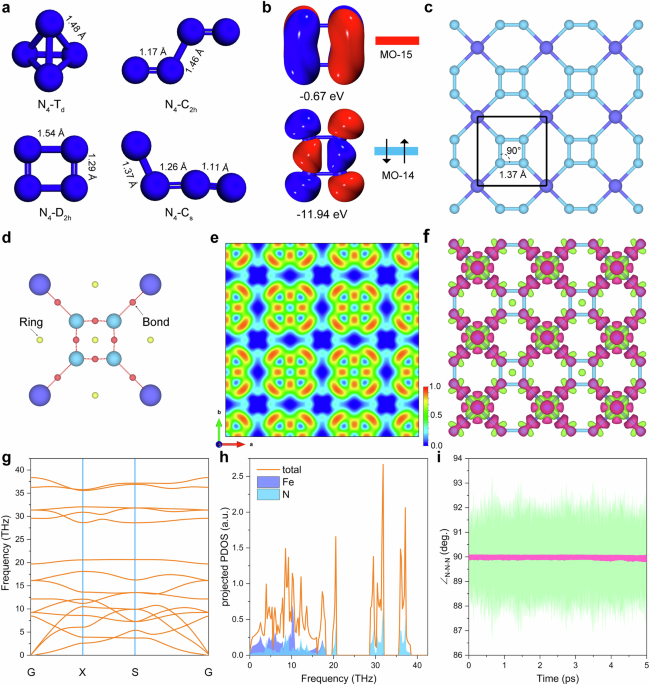
Perfect cyclo-tetranitrogen unit and chemical bonding
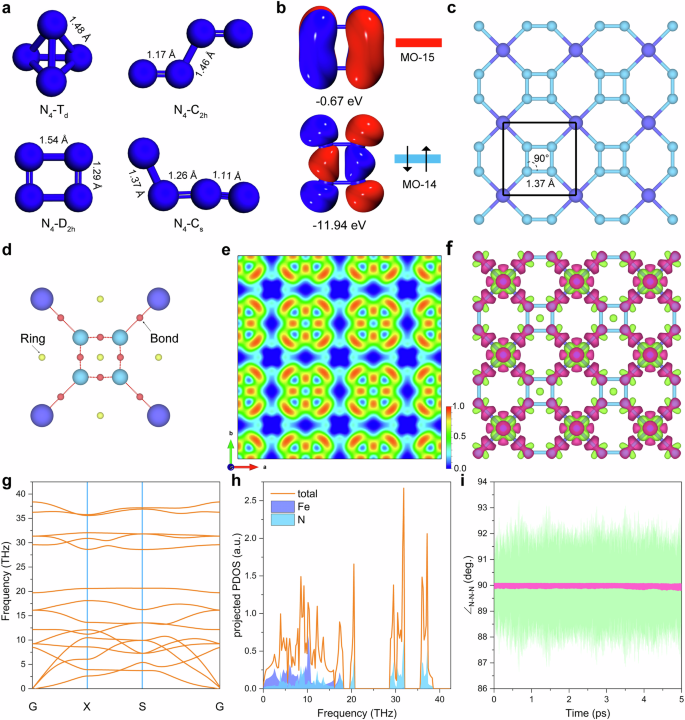
We first optimized the structure of N4 clusters with the molecular point groups of Td, D2h, C2h and Cs at B3LYP-D3/def2TZVP level and the results are shown in Fig. 1a. N4-D2h is identified as the metastable cluster and N4-C2h is found to be the most stable species (Supplementary Table 1). As illustrated in Fig. 1b, the D2h cyclo-N₄ cluster is a singlet ground state owing to its highest occupied molecular orbital (MO14), which exhibits significant N–N bonding character. Furthermore, one- and two-electron reductions populate the next orbital (MO15), thereby stabilizing the anionic species in with the elongated N–N bonds. However, once we embed the such D2h topology into the 2D periodic coordinated system with Fe, cyclo-N4 exhibits a perfect square motif with an optimized N − N bond length of 1.37 Å (PBE + U level), as shown in Fig. 1c and Supplementary Fig. 1. Additionally, calculations with several exchange–correlation functionals (Supplementary Table 2) consistently predict an N–N bond length of ~1.37 Å, which lies between the typical values for N = N double bonds (≈1.23 Å) and N–N single bonds (≈1.43 Å). For instance, at ambient pressure, the N = N bond in [N2]2- ions in BaN2 is 1.23 Å and the calculated N − N bond lengths in [N2]4- in PtN2 and OsN2 are 1.41 Å and 1.43 Å respectively19,20. Therefore, although the polymeric cyclo-N4 framework bonds have been reported in the cluster model and bulk compounds previously, the t-FeN4 monolayer possesses a unique single N − N bond with perfectly planar square N4 unit rarely observed/predicted in 2D confirmed space.
a The optimized structure of N4-Td, N4-D2h, N4-C2h, and N4-Cs. Bond lengths are given in angstrom. Values were obtained from B3LYP-D3/def2TZVP computations. b Frontier molecular orbitals of the neutral cyclo-N4 unit. c Crystal structure of t-FeN4 monolayer viewed along c-axis. The bond lengths are given in angstrom and bond angle in degree. d Critical points in the unit cell of the t-FeN4 monolayer (shown as smaller balls: bonds, red; rings, yellow). e Plot of the ELF map viewed from the vertical direction. ELF ranges from 0.0 (blue) to 1.0 (red). f Deformation density for the t-FeN4 monolayer. Red and green refer to electron accumulation and depletion regions. The isovalue is 0.005 e/Å3. g Phonon dispersion spectrum and (h) phonon density of states of the t-FeN4 monolayer. i Variation of the \({\angle }_{N-N-N}\) angle in t-FeN4 supercell as a function of the AIMD simulations. The green trace shows the \({\angle }_{N-N-N}\) angle values as recorded from the AIMD simulation, while the pink trace represents the fitted trend through data points.
An intriguing inquiry arises regarding the bonding character of such unique 2D (4.62)4(64) cpa topology21. It is of particular interest to determine if the cyclo-N4 specie form ionic bonds with the cations, or possibly coordination or covalent bonds. To address this, we conducted a Quantum Theory of Atoms in Molecules (QTAIM) analysis22. To study the bonding characteristics, we computed the Laplacian ∇2ρ(r) of the N − N and Fe−N bonds in the t-FeN4 monolayer structure, as depicted in Table 1. The corresponding bond critical points (BCPs) are shown in Fig. 1d. The type and strength of chemical bond can be characterized by the charge density the ρ(r) and the curvature ∇2ρ(r) at the BCP. The calculated values of ∇2ρ(r) for the N − N and Fe−N interactions are −0.897 a.u. and 0.505 a.u., respectively. According to established QTAIM criteria, A negative ∇2ρ(r) at the BCP, together with a relatively large ρ(r), is taken as a hallmark of shared‑electron (covalent) bonding, whereas a positive ∇2ρ(r) coupled with a smaller ρ(r) indicates a closed‑shell (ionic or coordination) interaction22,23. The results indicated that this value is between bulk AlN4 and Li2N4 (Supplementary Table 3), closely match the strongly negative value we observe, confirming robust N − N covalency of the structure. Next, the bonding character of t-FeN4 monolayer is further understand by electron localization function (ELF) mapping on the cyclo-N4 plane. Figure 1e and Supplementary Fig. 2 display a prominent accumulation of electron density between each nitrogen pair, confirming the presence of four N − N bonds in cyclo-N4. Meanwhile, the N lone pairs are assigned to regions around the four N atoms and bonded to adjacent Fe atoms, which exhibit moderate ELF values (<0.5), consistent with partial electron delocalization typical the bonds. Deformation-density plots show pronounced electron accumulation in the N − N bonding region and comparatively diffuse accumulation around Fe−N, corroborating the stronger covalent nature of N − N bonding and the mixed ionic/covalent nature of Fe−N bonding, as shown in Fig. 1f. Moreover, Crystal Orbital Hamilton Population (COHP) analyses (Supplementary Fig. 3) reveal large negative integrated COHP (–ICOHP) for N − N bonds (5.63 eV), indicating strong covalent character24. While the ICOHP value of 2.32 eV for Fe–N bond suggests moderate covalent character compared to N − N bonds. Bader charge analysis indicates that each Fe atom donates approximately 1.14 e to the nearby N atoms. This observation is also consistent with the deformation density plot, providing further confirmation of the charge redistribution within the t-FeN4 monolayer.
The stability of the t-FeN4 monolayer has been thoroughly validated through comprehensive analyses, including the calculated formation energy, phonon dispersion spectrum (Figs. 1g, h), ab-initio molecular dynamics (AIMD) simulations (Supplementary Fig. 4), and elastic constants (Supplementary Note 1 and Supplementary Table 4). Interestingly, the N4 ring retains a nearly perfect square configuration even at finite temperature, as shown in Fig. 1i and Supplementary Fig. 5, which indicates the high stability of the cyclo-tetranitrogen in the t-FeN monolayer. Detailed discussion of the structural energy stability, mechanical stability/properties, and the stability of the t-FeN4 structure under aqueous solution can be found in Supplementary Note 1 and Supplementary Figs. 6–9. Moreover, based on the recent empirical correlation proposed by Bondarchuk et al. for N5-containing systems, the decomposition temperature (\({T}_{{dec}}\)) can be estimated from the longest N–N bond length (\({l}_{N-N}\)) using the equation \({T}_{{dec}}(^\circ {\rm{C}})=-4073\times {[l}_{N-N}({\text{\AA }})]+5594.7\)25. For the t-FeN4 monolayer, we obtain \({T}_{{dec}}\) ≈ 15 °C. This estimate further supports the ambient-temperature stability of the cyclo-N4 unit in the t-FeN4 monolayer. Therefore, even energetically the MN4 structure with cyclo‑N4 unit represents a metastable configuration18, our multiscale computational analyses demonstrate that the proposed t‑FeN4 structure exhibits robust stability in both dynamical and thermodynamic dimensions.
Tuneable electrons and magnetic properties
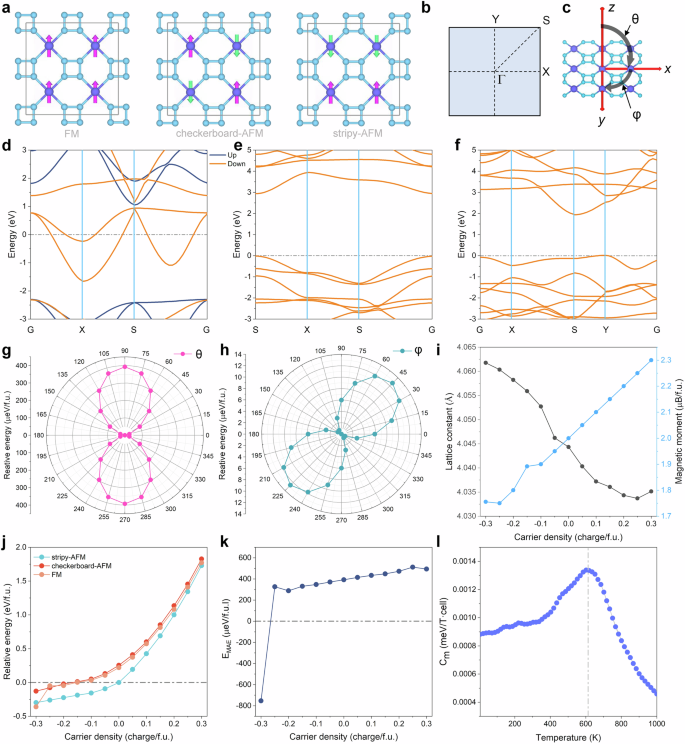
Beyond unique structural and chemical bonding properties, the 2D confinement induces emergent magnetic phenomena through spin-polarized t-FeN4 monolayer. We then investigated in detail the electronic structure and magnetic properties of the t-FeN4 monolayer structure. Using the supercell model, we evaluated three potential magnetic configurations (Fig. 2a) to identify the magnetic ground state of the t-FeN4 monolayer. These configurations included one ferromagnetic (FM) state and two antiferromagnetic (AFM) states (stripy-AFM and checkerboard-AFM, respectively). The relative energies of the different magnetic states, calculated using various methods, are summarized in Supplementary Table 5. Among them, the stripy-AFM state was determined to be the ground state. This energy difference is attributed to the competition between the ferromagnetic coupling of nearest neighbours and the antiferromagnetic coupling of next-nearest neighbours, emphasizing the delicate balance of exchange interactions in low-dimensional systems. The magnetism primarily originates from the Fe atom, as demonstrated by the spin charge density (Supplementary Fig. 10), with each Fe atom displaying a magnetic moment of 2.0 μB. Based on spin-polarized HSE06 functional, our band structure calculations reveal that, despite all configurations exhibiting semiconductor behavior, the FM state uniquely displays half-metallicity, as shown in Figs. 2b–f (cf. density of states using HSE06 functional and band structure using PBE + U functional in Supplementary Figs. 11–16). In the FM configuration, while the spin-down channel remains metallic, the spin-up channel develops an insulating gap of 3.39 eV. This pronounced asymmetry is associated with crystal field-induced splitting of the Fe3d orbitals, where the d-orbital plays a dominant role in the spin-down conduction near the Fermi level (Supplementary Fig. 17). Such behaviour is highly advantageous for spintronic applications, as it facilitates 100% spin-polarized transport, which is essential for efficient spin injection and detection26,27.
a Three different magnetic states: FM, checkerboard-AFM, and stripy-AFM, respectively. b Brillouin zone path with labelled high-symmetry k-points of the t-FeN4 monolayer. c Spin-orbit coupling (SOC) induced magnetic moment orientations, illustrating in-plane (φ) and out-of-plane (θ) anisotropy. d–f Spin-polarized band structures for the three magnetic states based on HSE06 functional. g, h MAE analysis reveals strong out-of-plane anisotropy compared to in-plane driven by SOC-mediated orbital rehybridization. i The lattice constant and magnetic moment of the t-FeN4 monolayer at different doping density. j The relative energy of three different magnetic arrangements and (k) MAE of t-FeN4 monolayer as a function of carrier density. l The specific heat as a function of temperature for the t-FeN4 monolayer.
Magnetic anisotropy energy (MAE) is another key factor in achieving long-range magnetic ordering in 2D materials, with higher MAE values indicating greater thermal stability of the magnetic state28,29,30. The MAE is quantified as the energy differential between in-plane (\({E}_{x}\)) and out-of-plane (\({E}_{z}\)) ferromagnetic orientations, expressed mathematically as \({MAE}={E}_{x}-{E}_{z}\). A positive MAE value signifies preferential alignment of the magnetization axis perpendicular to the plane (out-of-plane easy axis), while a negative MAE indicates in-plane magnetization dominance. This directional dependence arises from spin-orbit coupling effects that modulate orbital hybridization in the 2D confined geometry. The MAE values corresponding to rotations in the x–y and x–z planes are illustrated in Fig. 2g, h, respectively. The out-of-plane easy axis exhibits a remarkably high MAE of 393 μeV/f.u. (cf. Supplementary Fig. 18 for 3D schematic of MAE), surpassing values reported for prototypical 2D magnets such as CrI3 (24.68 μeV/f.u.)31, CrS2 (255.57 μeV/f.u.)32, and CoGa2S4 (47 μeV/f.u.)33.
We further investigate doping as a strategic approach to modulate its magnetic behaviour. As illustrated in Fig. 2i, electron doping induces lattice expansion, whereas hole doping drives contraction, a phenomenon attributable to charge-dependent Coulomb screening effects: Electron doping enhances interatomic repulsion via occupied antibonding states, whereas hole doping strengthens the Fe–N bonds by depleting electrons from bonding orbitals near the Fermi level. Notably, magnetic moments exhibit an inverse trend—electron doping suppresses the Fe-centered moment (from 2.0 μB to 1.75 μB), while hole doping enhances it (up to 2.3 μB at +0.3 e/f.u.). This dichotomy arises from doping-driven shifts in 3d-orbital occupancy, where electron filling reduces unpaired spins, whereas hole creation amplifies spin polarization. Remarkably, the stripy-AFM ground state persists across a broad doping range (−0.2 to +0.3 e/f.u.), as shown in Fig. 2j. Only under extreme electron doping (−0.3 e/f.u.) does the system transition to FM ordering, driven by weakened superexchange interactions and enhanced direct Fe–Fe ferromagnetic coupling. Crucially, AIMD simulations confirm structural integrity even at these doping extremes (Supplementary Figs. 19, 20), with no bond dissociation observed over 3 ps at 300 K. The doping strategy also enables precise control over magnetic anisotropy. For example, heavy electron doping reduces the MAE magnitude and eventually inverts its sign (−754 μeV/f.u. at −0.3 e/f.u.), switching the easy axis from out-of-plane to in-plane. This tunability stems from doping-induced redistribution of d-orbital populations, which modifies the relative contributions of second-order SOC terms. Such programmable magnetic anisotropy, coupled with ambient stability, positions t-FeN4 as a versatile platform for spin-orbit torque devices and non-volatile memory architectures, where electric-field-controlled doping could enable dynamic switching between distinct magnetic states.
For spintronic devices to function effectively under ambient conditions, their critical temperatures must exceed room temperature. To evaluate this critical parameter for the t-FeN4 monolayer, we performed large-scale Monte Carlo simulations based on the anisotropic Heisenberg model, explicitly accounting for both nearest-neighbor (J1) and next-nearest-neighbor (J2) exchange interactions (Supplementary Fig. 21). The interaction parameters, derived from spin-polarized PBE + U calculations, revealed strong antiferromagnetic coupling with J1 = − 0.85 meV and J2 = − 19.7 meV, where the dominant J2 term governs the stripy-AFM ground state through competing super-exchange pathways mediated by the N4 rings. The temperature-dependent magnetization curve (cf. Fig. 2l), obtained through finite-size scaling analysis of the 30 × 30 supercell, demonstrates a Néel temperature of 600 K—a value that not only exceeds room temperature but also surpasses some prototypical 2D magnets such as CrCl3 (10–17 K)34, FeCl2 (47 ± 8 K)35, FePS3 (120 K)36, CrMoC2S6 (556 K)37, etc. Therefore, the combination of ultrahigh Néel temperature and strong magnetic anisotropy suggests t-FeN4 could serve as a promising material for room-temperature spin logic gates, non-volatile magnetic memory, and other quantum-enhanced technologies requiring persistent magnetic ordering without cryogenic constraints28,38,39,40.
Construction of the MLP for t-FeN4 monolayer
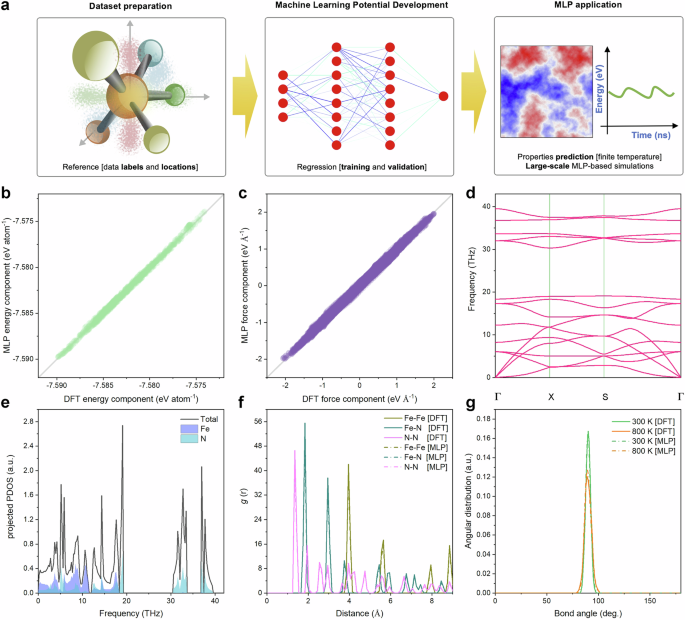
The demonstrated magnetic tunability motivates development of accurate computational tools for simulating realistic material configurations. However, traditional DFT-based approach becomes computationally prohibitive for studying temperature-dependent behaviour in extended systems containing more than thousands of atoms41,42. The workflow for constructing the MLP for the t-FeN4 monolayer and its subsequent application is comprehensively depicted in Fig. 3a. Detailed computational protocols for both the MLP construction and the AIMD simulations are provided in the Methods section and Supplementary Figs. 22–25. This dual approach is designed to rigorously assess the model’s capability to replicate critical properties—namely, the energies, forces, and structural configurations—which are essential for accurately reproducing the complex characteristics of the materials43.
a Flowchart of the training procedure of the MLP model. Comparison of (b) energy and (c) averaged atomic forces for the configurations from DFT and MLP. d Phonon dispersion and (e) phonon density of states of t-FeN4 monolayer computed with MLP. f The radial distribution function (RDF) for the Fe–Fe, Fe–N, and N–N distance in t-FeN4 monolayer at 300 K. Solid lines indicate AIMD simulations, whereas dashed lines show the results of MLP trajectories. g Same for the angular distribution functions (ADF) at 300 and 800 K, computed using a radial cut-off of 2.0 Å.
Figures 3b, c present a direct comparison between the MLP model predictions and density functional theory (DFT) calculations for the t-FeN4 monolayer. The results demonstrate excellent agreement, with the MLP model achieving a root mean square error (RMSE) of 14.1 meV per atom for energy and 0.016 eV Å−1 for forces. These low error margins underscore the high fidelity of the MLP in capturing the intricate interatomic interactions within the system43. Further, the dynamic stability of the FeN4 monolayer is substantiated by the phonon analysis presented in Fig. 3d, e. The phonon dispersion curves obtained via the MLP show no imaginary frequencies, a clear indication of the dynamic stability of the structure. The phonon density of states analysis reveals that the low-frequency vibrational modes are primarily attributed to the Fe–N bonds, whereas the high-frequency modes predominantly arise from the vibrations within the N4 ring. This nuanced understanding of the vibrational characteristics is critical for predicting the material’s thermal and mechanical behaviour.
Figure 3f compares the radial distribution functions (RDFs) computed from both AIMD and MLP-MD simulations for the t-FeN4 monolayer supercell. The RDF analysis provides valuable insights into the spatial correlations and local bonding environments, reflecting the accuracy with which the MLP model replicates the DFT-derived structural features. Complementing this, Fig. 3g illustrates the angular distribution profiles at various temperatures. Notably, at 800 K, the increased thermal perturbations result in a broader angular distribution—a phenomenon that is effectively captured by the MLP-based molecular dynamics simulations. This consistency across temperature regimes further validates the robustness of the MLP model.
Overall, the integration of MLP with both DFT and AIMD simulations not only validates the model’s accuracy in describing the fundamental properties of the t-FeN4 monolayer but also provides a powerful framework for exploring the material’s dynamic behaviour under varied conditions. This comprehensive approach is instrumental in advancing our understanding of complex material systems and paves the way for the rational design of novel materials with tailored properties.
Exceptional generalisation capability of the MLP for different patterns
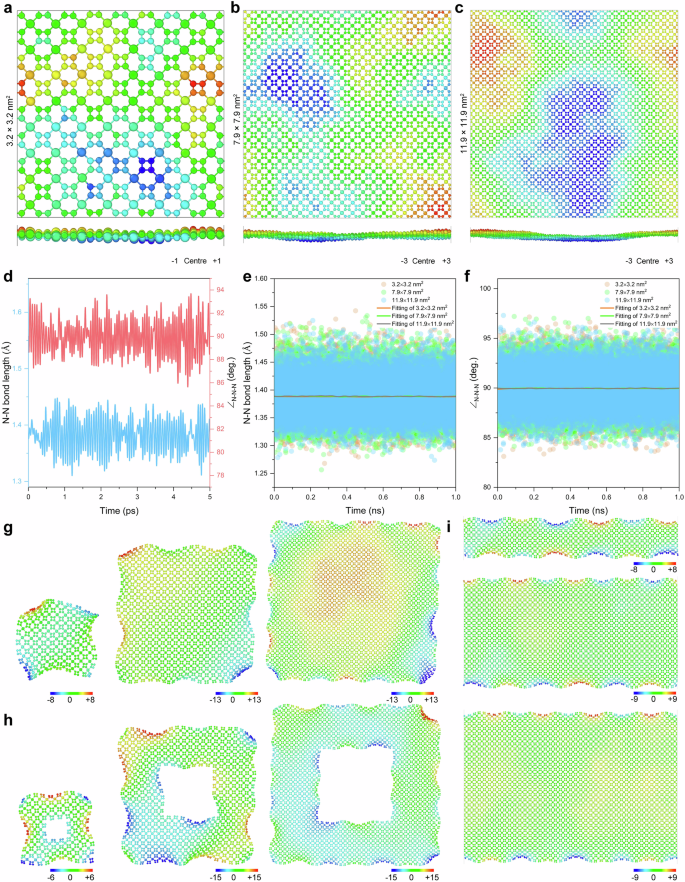
The generalisation capability of the MLP is critical to ensure prediction accuracy, transferability, robustness against overfitting, and uncertainty quantification, thereby facilitating further utilisation in materials discovery. Therefore, we first evaluated the performance of the well-trained MLP for periodic t-FeN4 structures of varying sizes, as illustrated in Figs. 4a–c and Supplementary Fig. 26. As the number of atoms increases, we observe a corresponding increase in the effective out-of-plane extension along the z-axis. This behaviour is primarily attributed to the cumulative effects of thermal fluctuations and minor surface reconstructions that become more pronounced in larger systems. Remarkably, despite these effects, the overall structural integrity is maintained even for systems as large as 57.0 nm2, indicating a robust stability of the t-FeN4 framework, as shown in Supplementary Figs. 27–29. To rigorously compare the MLP predictions with DFT results, we performed a 5-ps AIMD simulation under room temperature. The AIMD results, as shown in Fig. 4d, demonstrate that both the N–N bond lengths and bond angles remain almost perfectly square throughout the simulation. In our subsequent analysis, we applied the MLP to systems with different lattice sizes and directly compared the results to the AIMD benchmarks. As depicted in Figs. 4e, f, the MLP accurately reproduces the AIMD outcomes, yielding average N–N bond lengths of ~1.37 Å and bond angles of 90°. This high degree of correspondence confirms that the MLP possesses exceptional generalization capability; it accurately captures the thermodynamic and dynamic behaviour of the t-FeN4 monolayer across a range of system sizes, even when the extent of out-of-plane fluctuations increases with the number of atoms. To further test the transferability of the MLP, we systematically simulated various non-periodic t-FeN4 structures, including nanosheets, nanomatrices, and nanoribbons, as shown in Figs. 4g–i and Supplementary Figs. 30–32. Notably, these simulations encompass structures with edges and potential defect sites—configurations that were not included in the original training dataset of the MLP. Despite this, the MLP was able to reproduce high-precision finite-temperature behaviour across these diverse morphologies. The predicted structural parameters and dynamical evolution under finite temperature conditions closely match those obtained from AIMD, thereby reinforcing the reliability of the MLP across different dimensional scales and defect configurations.
Periodic t-FeN4 configurations with the system size of (a) 3.2 × 3.2 nm2, (b) 7.9 × 7.9 nm2, and (c) 11.9 × 11.9 nm2, respectively. Colour coding indicates the atomic positions in the direction normal to the layer. d Statistics of the N–N bond lengths and bond angles obtained from AIMD simulation at room temperature. e, f Statistical averages of the N–N bond length and bond angle obtained from the MLP-MD simulations at room temperature. g–i Systematic tests on t-FeN4 nanosheets, nanomatrices, and nanoribbons. Colour coding indicates the atomic positions in the direction normal to the layer.
These systematic studies provide compelling evidence for the exceptional generalization ability of the MLP. The model not only reproduces the essential structural and dynamical properties of periodic t-FeN4 monolayers, but also accurately simulates complex nanostructured systems that include edges, defects, and variations in atomic arrangement. Moreover, the MLP’s ability to efficiently simulate systems containing tens of thousands of atoms—while maintaining a high degree of accuracy—suggests that it can be effectively applied to large-scale atomistic simulations that are computationally prohibitive for conventional first-principles methods. The fact that even defected t-FeN4 structures and various nanostructures remain stable at finite temperatures suggests that these materials are intrinsically robust. This robustness indicates that t-FeN4 monolayers, with their unique structural and magnetic features, have a high likelihood of being successfully synthesized in the laboratory. Furthermore, the capability of the MLP to accurately predict the thermal, structural, and dynamic behaviour of these materials under realistic conditions can serve as a valuable guide for experimentalists aiming to design and fabricate novel low-dimensional magnetic systems for spintronic and magnetic storage applications.
In summary, we demonstrate a fundamental advance in polynitrogen stabilization strategies: 2D confinement in t-FeN4 monolayer ambiently stabilizes planar cyclo-N4 units through the combined action of geometric constraints and charge transfer, thus potentially achievable without high-pressure synthesis. The developed MLP exhibits excellent generalization across structural motifs—including extended monolayers, nanoribbons, and defective configurations—achieving quantum-mechanical accuracy while enabling large-scale simulations of temperature-dependent behaviour previously inaccessible to first-principles method. The emergent giant out-of-plane magnetic anisotropy and high Néel temperature, establish t-FeN4 as a tunable platform for designing spin-filtering devices and non-volatile memory elements. By elucidating how dimensional reduction suppresses N ≡ N bond reformation through orbital hybridization control, this work provides a generalizable blueprint for stabilizing metastable nitrogen topologies, while the validated MLP framework bridges critical gaps between quantum-level precision and mesoscale materials engineering, collectively advancing both polynitrogen chemistry and magnetic material design.
Considering that the positive example of the synthesis of 2D polynitrogen layers under high pressure9, it is expected that such 2D system can be prepared under ambient conditions in future studies. Our findings unveil an alternative design principle for the stabilisation of polynitrogen, whereby 2D confinement suppresses the bond dissociation pathways that are inherent to bulk systems. This approach may guide the development of ambient‑stable polynitrogen architectures without relying solely on high‑pressure approach, and could inform future efforts to synthesize functional polynitrogen materials.
Methods
Ab initio calculations
For different N4 species, the structure optimizations were carried out by using the B3LYP exchange-correlation functional44,45. All cluster calculations were performed in the Gaussian 09 program suite46. The def2-TZVP basis set47 was employed for nitrogen during structure optimizations. The DFT-D3 method48 was used to include the dispersion correction. All reported energies are obtained by single point energy calculations with G4 method49.
All the periodic DFT calculations were performed using the Vienna Ab initio Simulation (VASP, 5.3.2 version) package50. In these simulations, the projected augmented wave (PAW) method51 was adopted, and the generalized gradient approximation (GGA) in the form of the Perdew–Burke–Ernzerhof (PBE) functional52 was used for the exchange-correlation potential. We systematically evaluated the influence of different functionals (PBE, PBE + U, PBEsol, and B3LYP) on the lattice parameters, including both spin-polarized and non-spin-polarized calculations, which yielded comparable lattice constants (Supplementary Table 2). Hence, unless explicitly stated otherwise, all calculations presented here are based on DFT + U results. The on-site Coulomb interactions for localized d electrons in iron were treated using the Hubbard corrections following Dudarev’s approach53, with U = 4.0 eV and J = 1.0 eV chosen to reproduce experimental bulk FeN4 configuration11. An energy cutoff of 850 eV and a 12 × 12 × 1 Monkhorst–Pack k-point mesh (as determined by convergence tests, Supplementary Fig. S33) were used for Brillouin zone integrations. For an accurate band structure analysis, the hybrid Heyd–Scuseria–Ernzerhof (HSE06) functional54 was additionally employed, and spin–orbit coupling (SOC) effects were included in MAE calculations.
Electron charge density analysis
The electron charge density was analyzed topologically for t-FeN4 monolayer using the Quantum Theory of Atoms in Molecules (QTAIM) approach22. This theory defines a solid using a zero-flux surface of the electron density gradient ∇ρ(r). The charge density distribution ρ(r) and its principal curvatures (eigenvalues of the Hessian matrix) at the bond critical point (BCP) provide insight into bonding type and properties. The second derivative of the electron density (Laplacian) ∇²ρ(r) reveals electron concentration at the BCP. Results showed a direct correlation between ∇ρ(r) and ∇²ρ(r) at the BCP and bond order and strength. Electron localization function (ELF) ranges from 0 to a maximum of 1, with values close to 1 indicating localized electrons. High ELF values are seen in bonds, cores, and lone pairs, with maxima appearing in the middle of bonds (e.g., the N-N bond in N2 molecule).
Training data preparation
The finite temperature ab initio molecular dynamics (AIMD) simulations were performed to generate datasets for machine learning training by using time steps of 1 fs in 4 × 4 × 1 supercell (containing 80 atoms) of t-FeN4 monolayer. Then the supercell structure was simulated by the Nosé–Hoover thermostat55 in an NVT (N-number of particles, V-Volume, and T-temperature) ensemble. The Brillouin zone was sampled with a 1 × 1 × 1 Monkhorst−Pack k-points grid56. We performed three different AIMD simulations by considering the different temperatures of 300, 500, and 800 K, to assess the impact of the temperature. The total dataset consists of around 30,000 configurations.
MLP training and validation
The smooth version of the DeePMD model with an inner cutoff of 1 Å and an outer cutoff of 6.9 Å was adopted in this work, and the DeePMD-kit package57 was used for training and validation. The embedding network has the ResNet-like architecture58 with a size of (25, 50, 100).
MLP-based MD simulations
For MD simulations, an optimized interface of DeePMD potential has been implemented in the Large-scale Atomic/Molecular Massively Parallel Simulator (Lammps) molecular dynamics package59. All subsequent simulation through the DeepMD protentional was carried out by Lammps code with Nosé-Hoover style thermostat. The timestep in all MD simulations was 1 fs. We performed the ns-level MD simulation at 300 K temperature for the deferent 2D systems with the different atomic numbers (from 320 to 103,680 atoms) and different structural types, covering ideal periodic configurations, nanoribbons, nanosheets, and nanosheets with defects. (cf. Figure 4 and Supplementary Figs. 26–32).
Phonon calculation
The phonon properties were computed using two python-based tools: phonopy for VASP and phonoLAMMPS for LAMMPS50,59,60. The phonon bands for the 19 × 19 supercell of t-FeN4 monolayer were first calculated with a 12 × 12 × 1 mesh point sampling of the Brillouin-zone. The partial phonon density of states (Ph DOS) was then obtained from the calculations.
Visualization
MD trajectories and model structures were visualized using VESTA and OVITO software61,62.
Data availability
No datasets were generated or analyzed during the current study. The central codes used in this paper are VASP and DeePMD-kit. Detailed information related to the license and user guide are available at https://www.vasp.at and https://github.com/deepmodeling/deepmd-kit.
Code availability
The central codes used in this paper are VASP and DeePMD-kit. Detailed information related to the license and user guide are available at https://www.vasp.at and https://github.com/deepmodeling/deepmd-kit.
References
Christe, K. O. Polynitrogen chemistry enters the ring. Science 355, 351–351 (2017).
Mailhiot, C., Yang, L. H. & McMahan, A. K. Polymeric nitrogen. Phys. Rev. B 46, 14419–14435 (1992).
Lide, D. CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data. (CRC press, 1995).
Wang, Y. et al. Stabilization of hexazine rings in potassium polynitride at high pressure. Nat. Chem. 14, 794–800 (2022).
Xu, M., Li, Y. & Ma, Y. Materials by design at high pressures. Chem. Sci. 13, 329–344 (2022).
Nguyen, M. T. Polynitrogen compounds. Coord. Chem. Rev. 244, 93–113 (2003).
Bondarchuk, S. V. Recoverability of N4x– Anions to Ambient Pressure: A First-Principles Study of cyclo - and syn -Tetranitrogen Units. J. Phys. Chem. C. 125, 7368–7377 (2021).
Xu, Y. et al. Taming cyclo-pentazolate anions with a hydrogen-bonded organic framework. Commun. Mater. 5, 25 (2024).
Aslandukov, A. et al. Stabilization of N6 and N8 anionic units and 2D polynitrogen layers in high-pressure scandium polynitrides. Nat. Commun. 15, 2244 (2024).
Zhai, H. et al. Stabilized Nitrogen Framework Anions in the Ga–N System. J. Am. Chem. Soc. 144, 21640–21647 (2022).
Bykov, M. et al. Fe-N system at high pressure reveals a compound featuring polymeric nitrogen chains. Nat. Commun. 9, 2756 (2018).
Eremets, M. I., Gavriliuk, A. G., Trojan, I. A., Dzivenko, D. A. & Boehler, R. Single-bonded cubic form of nitrogen. Nat. Mater. 3, 558–563 (2004).
Bykov, M. et al. High-Pressure Synthesis of Dirac Materials: Layered van der Waals Bonded BeN 4 Polymorph. Phys. Rev. Lett. 126, 175501 (2021).
Bykov, M. et al. Realization of an Ideal Cairo Tessellation in Nickel Diazenide NiN2: High-Pressure Route to Pentagonal 2D Materials. ACS Nano 15, 13539–13546 (2021).
Liu, D. et al. Prediction of single-atom-thick transition metal nitride CrN4 with a square-planar network and high-temperature ferromagnetism. Phys. Rev. B 106, 125421 (2022).
Mortazavi, B., Shojaei, F. & Zhuang, X. Ultrahigh stiffness and anisotropic Dirac cones in BeN4 and MgN4 monolayers: a first-principles study. Mater. Today Nano 15, 100125 (2021).
Li, F. et al. Benzene-like N6 rings in a Be2N6 monolayer: a stable 2D semiconductor with high carrier mobility. J. Mater. Chem. C. 5, 11515–11521 (2017).
Zhang, S. et al. Two-dimensional binary transition metal nitride MN4 (M = V, Cr, Mn, Fe, Co) with a graphenelike structure and strong magnetic properties. Phys. Rev. B 106, 235402 (2022).
Wessel, M. & Dronskowski, R. Nature of N−N Bonding within High-Pressure Noble-Metal Pernitrides and the Prediction of Lanthanum Pernitride. J. Am. Chem. Soc. 132, 2421–2429 (2010).
Chen, Z. W. et al. Crystal structure and physical properties of OsN 2 and PtN 2 in the marcasite phase. Phys. Rev. B 75, 054103 (2007).
Alexandrov, E. V., Blatov, V. A. & Proserpio, D. M. How 2-periodic coordination networks are interweaved: entanglement isomerism and polymorphism. CrystEngComm 19, 1993–2006 (2017).
Bader, R. F. W. & Nguyen-Dang, T. T. Quantum Theory of Atoms in Molecules–Dalton Revisited. Adv. Quant. Chem.14, 63–124 (Elsevier, 1981).
Alikhani, M. E. On the chemical bonding features in boron containing compounds: a combined QTAIM/ELF topological analysis. Phys. Chem. Chem. Phys. 15, 12602 (2013).
Müller, P. C., Reitz, L. S., Hemker, D. & Dronskowski, R. Orbital-based bonding analysis in solids. Chem. Sci. 16, 12212–12226 (2025).
Bondarchuk, S. V. Structure enhancement of energetic materials: A theoretical study of the arylamines to arylpentazoles transformation. FirePhysChem 1, 190–197 (2021).
Son, Y.-W., Cohen, M. L. & Louie, S. G. Half-metallic graphene nanoribbons. Nature 444, 347–349 (2006).
Wolf, S. A. et al. Spintronics: A Spin-Based Electronics Vision for the Future. Science 294, 1488–1495 (2001).
Rimmler, B. H., Pal, B. & Parkin, S. S. P. Non-collinear antiferromagnetic spintronics. Nat. Rev. Mater. 10, 109–127 (2024).
Misiorny, M., Hell, M. & Wegewijs, M. R. Spintronic magnetic anisotropy. Nat. Phys. 9, 801–805 (2013).
Modic, K. A. et al. Scale-invariant magnetic anisotropy in RuCl3 at high magnetic fields. Nat. Phys. 17, 240–244 (2021).
Webster, L. & Yan, J.-A. Strain-tunable magnetic anisotropy in monolayer CrCl3, CrBr3, and CrI3. Phys. Rev. B 98, 144411 (2018).
Xu, L.-Y., Jiang, P., Liu, L., Huang, H.-M. & Li, Y.-L. Strain-tunable magnetic phase transition and magnetocaloric effect in the CrS2 monolayer with bipolar magnetic semiconducting characteristics. Phys. Rev. B 111, 205407 (2025).
Zhang, S., Xu, R., Duan, W. & Zou, X. Intrinsic Half-Metallicity in 2D Ternary Chalcogenides with High Critical Temperature and Controllable Magnetization Direction. Adv. Funct. Mater. 29, 1808380 (2019).
Wu, J., Wu, H. & Tan, P. Magneto-Optical Interactions in Layered Magnets. Adv. Funct. Mater. 34, 2312214 (2024).
Tiwari, S., Van De Put, M. L., Sorée, B. & Vandenberghe, W. G. Critical behavior of the ferromagnets CrI3, CrBr3, and CrGeTe3 and the antiferromagnet FeCl2: A detailed first-principles study. Phys. Rev. B 103, 014432 (2021).
McCreary, A. et al. Quasi-two-dimensional magnon identification in antiferromagnetic FePS3 via magneto-Raman spectroscopy. Phys. Rev. B 101, 064416 (2020).
Wang, P., Wu, D., Zhang, K. & Wu, X. Two-Dimensional Quaternary Transition Metal Sulfide CrMoA2S6 (A = C, Si, or Ge): A Bipolar Antiferromagnetic Semiconductor with a High Néel Temperature. J. Phys. Chem. Lett. 13, 3850–3856 (2022).
Dal Din, A., Amin, O. J., Wadley, P. & Edmonds, K. W. Antiferromagnetic spintronics and beyond. npj Spintronics 2, 25 (2024).
Šmejkal, L., MacDonald, A. H., Sinova, J., Nakatsuji, S. & Jungwirth, T. Anomalous Hall antiferromagnets. Nat. Rev. Mater. 7, 482–496 (2022).
Shao, D.-F. & Tsymbal, E. Y. Antiferromagnetic tunnel junctions for spintronics. npj Spintronics 2, 13 (2024).
Rogge, S. M. J., Borgmans, S. & Van Speybroeck, V. Absorbing stress via molecular crumple zones: Strain engineering flexibility into the rigid UiO-66 material. Matter 6, 1435–1462 (2023).
Wang, Q. et al. A Theoretical Perspective for Ammonia Synthesis: Nitric Oxide or Nitrate Electroreduction?. Small Methods 9, 2401208 (2025).
Morrow, J. D., Gardner, J. L. A. & Deringer, V. L. How to validate machine-learned interatomic potentials. J. Chem. Phys. 158, 121501 (2023).
Lee, C., Yang, W. & Parr, R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789 (1988).
Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Frisch, M. J. Gaussian 09 Program. (2009).
Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 8, 1057 (2006).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006).
Chan, B., Deng, J. & Radom, L. G4(MP2)-6X: A Cost-Effective Improvement to G4(MP2). J. Chem. Theory Comput. 7, 112–120 (2011).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 57, 1505–1509 (1998).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Hoover, W. G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697 (1985).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Wang, H., Zhang, L., Han, J. & E, W. DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 228, 178–184 (2018).
He, K., Zhang, X., Ren, S. & Sun, J. Deep Residual Learning for Image Recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 770–778 (2016).
Thompson, A. P. et al. LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022).
Carreras, A. Phonolammps. phonoLAMMPS https://github.com/abelcarreras/phonolammps.
Momma, K. & Izumi, F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 41, 653–658 (2008).
Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18, 015012 (2010).
Acknowledgements
The authors thank prof. Sergey V. Bondarchuk for sharing the bulk structure containing cyclo-tetranitrogen units. The authors acknowledge the financial support from Chongqing Jiaotong University (No. F1240018) and Chongqing Graduate Tutor Team Construction Project (JDDSTD2022006). P.L. would like to thank the support from the Hunan Provincial Natural Science Foundation of China (2023JJ40621). Computing resources were provided by the National Supercomputer Centre (TianHe-3K) in Tianjin. The work also partially supported by e-INFRA CZ (ID:90140) for providing computational resources.
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Fan, D., Zheng, K., Li, H. et al. Machine learning augmented design of 2D magnet with planar cyclo-tetranitrogen: ambient thermal stability from quantum to mesoscale. npj Comput Mater 11, 286 (2025). https://doi.org/10.1038/s41524-025-01763-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-025-01763-7