基于忆阻器的物理不可克隆函数（PUF）抵抗机器学习攻击的韧性评估

智能系统目前影响着人们日常生活的多个方面，需要设备之间的高度连接和大量数据传输。应用程序与工业、城市和商业的融合提高了服务质量，并促进了制造和生产领域的扩展；因此，如今各个年龄段的人们倾向于使用智能应用来满足他们的日常服务需求。资源受限环境和物联网系统对数字化世界中日常生活的影响是显著的。这些系统需要大量的设备连接、复杂的计算以及大量的数据传输。物联网设备容易遭受数据丢失，因此在物联网平台和网络中，高效的加密原语对于保证机密性和认证至关重要。当构建以保密性、身份验证和完整性为重点的加密原语和安全解决方案时，加密随机性扮演着关键属性的角色。这些用于多个关键数字基础设施和硬件安全领域。随着诸如忆阻器等新兴纳米技术的出现，为构建一个占用面积小、成本低且功耗低的轻量级PUF（物理不可克隆功能）提供了有力的机会，这是我们在这篇论文中所解决的问题。得益于细胞结构方面的创新氧化铪基于的忆阻器在电气性能和功耗方面优于CMOS技术。请注意，句子开头的“-based”可能缺少一个关键术语或上下文信息，在这里保持原样以避免添加不必要的内容。如果这是一个特定的技术描述，请提供完整的信息以便更准确地翻译。原文：_based memristors show better electrical performance and lower power consumption compared to CMOS technology.氢氧化铪被提出作为最有前景的忆阻器材料之一，表现出高耐久性和热力学变化的韧性¹由于高的k介电常数强度导致\(HfO_2\)寄生电容效应被最小化，从而减少了功率损耗。最重要的是，\(HfO_2\)基于的忆阻器由于其简单的设计和卓越的可扩展性，与CMOS技术兼容。不同的研究提出了忆阻器PUF（物理不可克隆功能），这是因为制造过程中固有的随机性和称为周期到周期(C2C)变化的独特签名导致的，这将在以下部分进行解释。^2,3.

物理不可克隆函数（PUF）是物联网设备中一种有前景的轻量级加密原语，因为在内存受限的环境中如物联网中，它们不需要存储加密密钥的记忆体。随着技术的进步，低成本和低功耗的PUF设计已被提出。PUF的加密强度依赖于其响应随机性的质量。PUF的输入与输出之间的关系通常通过挑战-响应对（CRP）来区分，用于评估PUF生成真正随机且安全输出的能力。为了评估PUF响应的加密强度，必须根据包含唯一性、均匀性和扩散性测试的一系列指标进行验证。在唯一性测试中，我们评估具有相同设计和制造工艺的两个PUF之间的差异，理想情况下，对于相同的输入挑战，两个PUF的输出响应应有50%的不同。另一方面，均匀性是衡量PUF随机性的指标，在此指标下，PUF应该分布为等概率的0或1各占50%。最后，扩散性评估施加给同一PUF的不同挑战之间的响应向量差异，理想情况下这个值应该是50%，即为响应向量长度的一半。

相关工作和贡献

过去十年来，文献中提出了几种PUF设计。^4,5硅（CMOS）PUF包括仲裁器PUF⁶环振荡器物理不可克隆函数（RO-PUF）⁷，SRAM PUF⁸感放大PUF⁹，蝴蝶PUF¹⁰诸如仲裁PUF、XOR仲裁PUF和RO PUF等强PUF在攻击者可以访问CRP来训练数学模型时容易受到建模攻击。^{11,12,13,14,15}几个设计基于基于内存的PUF技术，如绝缘体上硅(SOI)晶体管技術。¹⁶和忆阻器^17,18,19SOI 和忆阻器技术利用一种称为记忆效应的独特效果，这种效应依赖于嵌入这两种技术中的高k介电绝缘层。记忆效应会导致单元电阻根据前一周期电流值的记忆发生变化。因此，由于内在物理特征的随机性，忆阻器的电阻值是随机的。不同的作者^2,3利用忆阻器I-V特性中的夹持回滞效应的C2C签名创建了真正的随机数生成器。忆阻器具有相对简单的架构，包括两个电极之间的氧化层，这种简单的设计使其能够与CMOS技术兼容。由于这种可扩展性，在制造CMOS器件所需相同晶圆区域的情况下，可以制作更多的忆阻器。忆阻器与CMOS技术的兼容性已经得到了证实。²⁰通过在同一晶圆上制造忆阻器交叉阵列器件和硅MOSFET。在¹⁹作者研究了一种忆阻式读写PUF，并实现了两个Al/CUxO/Cu器件，展示了横向切换特性，然而其中的一个器件却固定在了低电阻状态（LRS）。_in_¹⁸作者继续进行工作在¹⁹并展示了N位读写忆阻器PUF，通过测量唯一性、均匀性和比特别名来衡量M-PUF的统计质量。提出了一种基于TRNG的忆阻器PUF。²¹提供一种高质量熵和小型面积的轻量级密码学原语，无需任何后处理算法或电路。然而，尚未研究进一步的统计测试和建模攻击。_in_²²作者提出了混合忆阻器-CMOS PUF电路，其设计面积低于仅使用CMOS的PUFs。作者利用忆阻器器件中的延迟变化来生成特定实例的签名。作者验证了所提出的混合PUF对抗两种机器学习攻击LR和SVM的安全性。进一步构建了使用机器学习技术的高级工具以克隆PUF行为，预测未知挑战的响应。在本文中，我们研究了制造的基于忆阻器的PUF（MR-PUF）的随机性和可靠性。¹⁷基于集成忆阻器内快速且非线性的制造变化。表1总结了这项研究的主要贡献，即进行了一项全面的研究，专注于攻击随机数输出的弹性。这是基于使用逻辑回归（LR）、支持向量机（SVM）、高斯混合模型（GMM）和K均值算法构建随机性预测器。\(++\)随机森林和优化的分布式梯度提升模型（XGBoost）、高效时间内的长短时记忆网络（LSTM），以及数据复杂性。我们的结果在低准确性和接收者操作特征（ROC）方面分别为0.49–0.52和0.49–0.52，这表明无法预测随机数据，因此证明了MR-PUF的高效随机性预测弹性。对于我们的数据：使用了5032个训练样本与2157个测试样本来验证我们PUF的随机性。

加密原语设计和框架的内容见“MR-PUF架构”，加密随机性的强度通过几个指标和NIST统计测试进行评估。随机性评估”. “基于忆阻器的物理不可克隆函数机器学习分析工具“提供了用于构建分析和攻击方法论的机器学习分析框架和工具的描述，以及对随机输出弹性的测试结果的相关分析和讨论展示在”部分中。结果与讨论”.

忆阻器由于其随机性已成为物理不可克隆函数（PUF）的重要随机源。它们最初被引入于²⁶基于对称性要求，时间积分的电压（磁通量）与电荷之间必须存在某种关系。因此，忆阻器被定义为第四种电路特性，并且其数学模型表明忆阻器的电阻取决于电流之前的值。在测试中的忆阻器当在其顶部和底部电极上施加正电压时表现出双极开关行为：从高电阻状态（HRS）切换到低电阻状态（LRS），而在施加负极性时则从LRS切换回HRS。这种动态特性引入了较大的开关窗口，提供了较高的HRS/LRS比值，并且随着技术的不断进步，忆阻器的短OFF/ON开关时间可以达到120/20ns。²⁷.

(a忆阻器设计制造，bMR-PUF操作。

MR-PUF架构

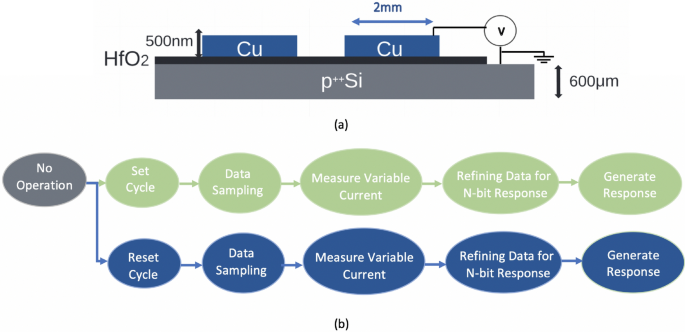
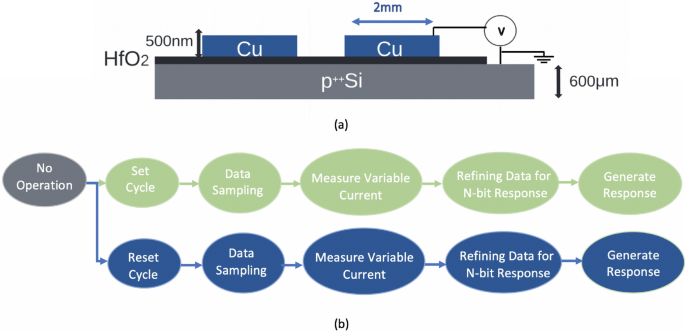
工作进行中¹⁷利用了C2C忆阻器签名特征和高HRS/LRS比值来生成真正的随机数。忆阻器设计如图所示。1它是在高度掺杂的基底上制造的\(p^{++}\)硅用作底电极，\(HfO_{2-x}\)用作开关介质/绝缘体，和Cu作为顶电极。为了在忆阻器上施加电压扫描，将底电极接地，并对顶电极施加电压扫描。使用Keithley 4200-SCS 参数分析仪来表征I-V曲线。

图中展示了PUF操作。1b.通过在每个周期中利用忆阻器的随机阈值电压，我们生成了一串用于响应的随机数。首先进行正向电压扫描，在根据随机阈值电压使忆阻器进入低电阻状态（SET操作模式）之后，对采样的变量电流进行测量，然后精炼数据以生成位字符串响应。对于负向电压扫描（复位周期），同样的分析如图所示。1.

(a均匀性 51.1% '1' 和 48.9% '0'。b一个显示响应0和1的灰度位图，c独特性 49.4% , (d扩散度 49.6%。

随机性评估

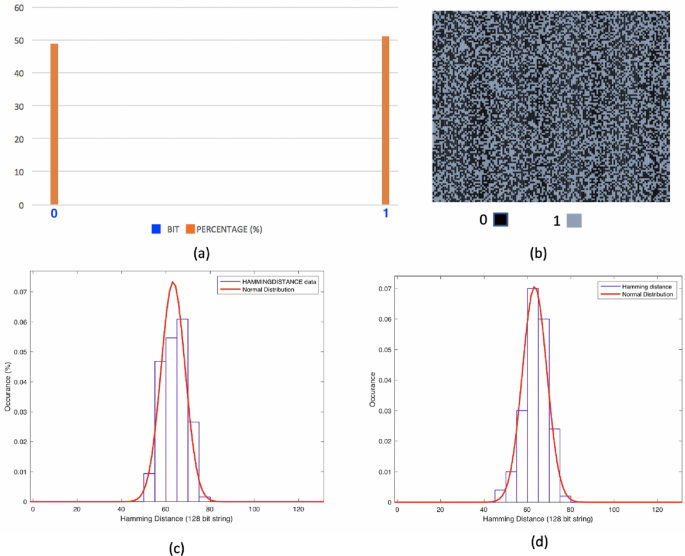
我们最初通过评估随机性和可靠性的主要标准指标（如实例间的汉明重量和汉明距离）来评估MR-PUF的密码学随机性，以计算MR-PUF的扩散性、唯一性和均匀性。为了评估均匀性和扩散性，我们应用了100个不同的挑战集，每个包含\(2^7\)比特到一个MR-PUF，以及_the_这个词在这里可能是多余的，如果是这样的话则忽略不译。如果要求包含_the_但没有其他含义，则保留_the_不出现在翻译中。原文： bits to one MR-PUF, and the\(2^7\)单个响应位连接形成一个128倍数的比特响应。PUF响应中“1”和“0”的百分比均匀性分别如图所示为51.1%和48.9%。2a，b展示了灰度位图，显示了0和1的响应。为了评估唯一性，我们使用了100个不同的MR-PUF实例，并评估了来自不同MR-PUFs对相同挑战的响应之间的海明距离（HD）。我们在研究中计算出的平均值为128位中的63.3位，如图所示，这接近50%。2c. 我们的研究计算了扩散性，以评估使用同一PUF对不同挑战所得到的响应向量之间的差异。如图所示，响应之间的HD值被计算为49.6%，接近理想的50%值。2为了进一步确保加密随机性强度，使用NIST 800-22测试中的15个测试对MR-PUF响应进行了加密学上的随机性测试，如表所示。2.

在接下来的部分中，我们将进一步研究通过应用针对增加NIST测试的MR-PUF输出随机性可预测性的机器学习分析和攻击工具所构建的MR-PUF的鲁棒性。

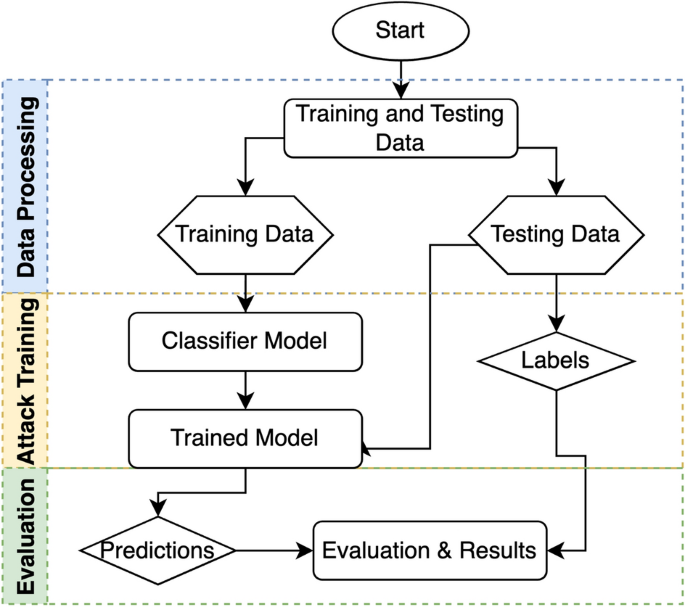
本文通过机器学习（ML）分析展示了MR-PUF对抗建模攻击的加密强度。用于检测攻击的机器学习框架包含几个子过程，如图所示。3首先，收集环境提供的数据并进行数据采样精炼。在数据采样子过程中，将数据分为训练集和测试集。我们分别选择了70/30的数据划分比例用于训练集和测试集。为了确保分析的全面性，我们从不同的类别中选取了机器学习架构。我们的目标是使用跨越监督、无监督以及深度学习等方法谱系的各种模型架构的机器学习方法。在监督学习范式下，模型通过寻找标记训练数据中的模式和关系来学习将输入变量映射到期望输出。在训练过程中，模型试图最小化其预测输出与真实输出之间的差异。无监督学习的目标是在没有任何明确指导的情况下找到数据中隐藏的模式、结构或关联性。无监督学习算法旨在聚类相似的数据点或发现有意义的数据表示。对于监督学习，我们希望采用经典强大的模型如LR和SVM，基于树的方法如RF和XGboost，以及通过MLP和LSTM进行深度学习。从无监督学习方面，我们专注于使用Kmeans++和概率性高斯混合模型（GMM）进行聚类。

基于文献的机器学习分析构建攻击模型

作者在²⁸在2004年首次证明了机器学习攻击对强PUF构成了重大威胁。几项研究提出了不同的技术来建模强PUF。^{11,12,13,14,15}针对此类攻击所提出的防御措施可以归类为结构非线性化^29,30,31以及CRP混淆技术^32,33然而，大多数的非线性化和CRP混淆技术降低了PUFs的可靠性，并且无法防御高级机器学习方法。因此，在本文中，我们将在不使用后处理算法的情况下测试MR-PUF在机器学习攻击下的鲁棒性，仅仅依赖于前一节所解释的忆阻器的真实随机性。Memristive Crossbar PUF的稳健性如所示²³经过SVM(RBF)和LR验证。这些攻击针对忆阻交叉棒的原始准确率分别为99%和96.8%。在作者提出了两种进一步的操作XOR和列交换以增强忆阻PUF的随机性之后，SVM(RBF)和LR攻击的准确率分别降至57%和49%。文中作者²⁴介绍了几种在文献中先前提出的PUF所面临的不同的机器学习攻击，以评估它们的脆弱性。作者实现了忆阻器仲裁PUF³⁴并评估了Memristor仲裁PUF对随机森林攻击的鲁棒性。该随机森林攻击达到了70%的准确率，证明了所提出的忆阻器的鲁棒性。³⁴对抗ML攻击。在²⁵作者提出了一种基于忆阻器的物理不可克隆功能（PUF），并结合了洛伦兹装置以增强其随机性。当验证其忆阻器对SVM和LR攻击的抵抗力时，他们显示出了接近50%的准确率。然而，添加洛伦兹设备增加了忆阻器设计的成本。这项研究的主要贡献是建立了一个经验性的机器学习分析和攻击工具，用于测试MR-PUF随机输出的抗攻击能力。本文的主要目的是验证MR-PUF设计的抵抗力，并确保其设计的密码安全性。我们的结果来自实际制造的忆阻器，而不是像其他出版物中所反映的那样来自模拟的忆阻器。

机器学习分析被重复应用于多个物理不可克隆函数（PUF）实例，以确保低建模准确率是可以重现的，并且该PUF对论文中应用的机器学习算法具有抗性。对安全原语进行建模攻击的基本思想如图所示。3我们的ML攻击的复杂性如表所示。4，其中k是聚类的数量，d是数据维度，n是训练集中的样本数量，和l是迭代次数。对于深度学习模型（MLP、LSTM），理论上限是根据之前分析界限的文献估计的。m以及n描述反向传播步骤中的运算次数。对于LSTM的反向传播和更新运算次数。T是序列长度，\(d_i\)和\(d_h\)这些是隐藏状态和输入的维度，在反向传播步骤中的计算成本比前馈更高。由于我们的LSTM也有一个MLP头，我们也增加了它的复杂性。一般来说，随着更大深度学习模型的复杂性的增加，准确估计上限变得不可能。因此，一种常见的方法是通过提供模型架构、计算硬件以及通过训练和推理时间来描述计算复杂性作为效率度量。对深度学习架构复杂性的详细分析超出了本文的研究范围。对于那些在训练时间和推理时间上有显著差异的模型，实际的计算时间复杂性会单独给出，这些时间测量是在最佳发现超参数设置下的模型。当前用于本研究的设置显示了运行时复杂性如表所示。4.

数据集

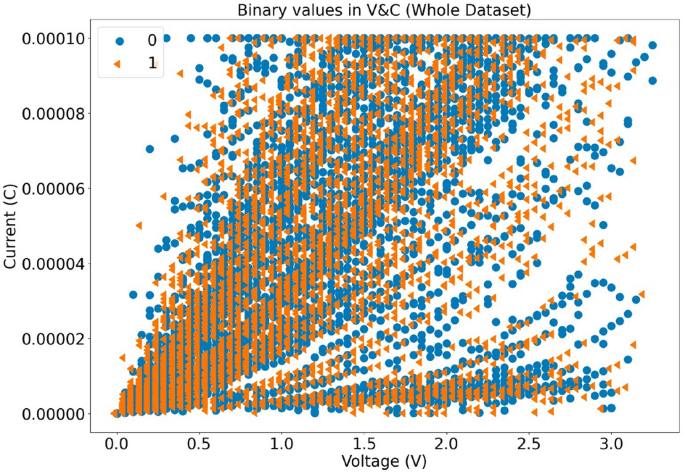
对于我们的人工智能模型，我们构建的数据集总共有7189行。每一项记录包含\[ [电流, 电压] \]成对的数据加上一个0或1的标签，该标签代表从忆阻器中提取的二进制位值。接下来，我们进行了划分以生成训练集和测试集。生成的测试集占总数据集的30%。MR-PUF产生的输出位数超过了我们使用的数据集大小。我们根据最常见的安全级别位数选择了数据集大小。

通用攻击管道。

逻辑回归

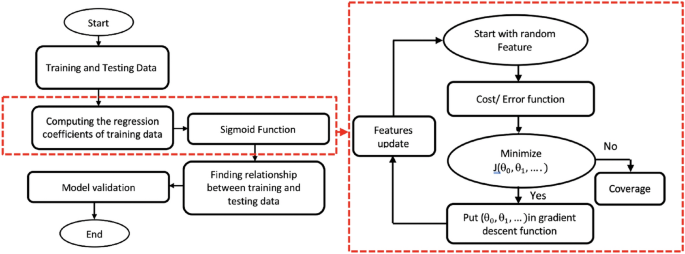
逻辑回归³⁵使用逻辑函数来分析数据集并预测二元结果，如图所示。4逻辑回归通过分析数据集并使用sigmoid函数为该研究中的每个数据点分配一个概率来进行分析。\(h_{\Theta}(X)=\frac{1}{1+e^{-(\Theta^TX)}}\)每个数据点的成本或误差是\(\cos(h_{\theta}(x), y)\)总成本是每个数据点误差的总和，定义为\(J(\theta)=(1/k)\sum _{i=1}^{k} (Cost(h_\theta (x^{(i)}),y^{(i)}))\)我们目标是使这个成本函数最小化\(J(\theta)\)使用梯度下降算法，如图所示。4在每次迭代中，所有的特征参数\(\theta _j\)利用这个方程进行持续调整\(\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta)\).

逻辑回归流程图。

支持向量机(SVM)

支持向量机（SVM）可以执行二分类任务，并通过在由支持向量创建的间隔上进行划分来解决分类问题。利用核函数，SVM可以将已知的训练样本映射到更高维的空间中。³⁶分离超平面应尽可能与不同分类的所有向量保持最大距离。离分离超平面最近的向量称为支持向量。向量之间的距离称为间隔。构建一个好的SVM的关键是在最小化分类错误的同时最大化间隔。训练过程由正则化系数调节。λ如上所述，为了找到数据的非线性分离，通常会使用常用的核函数：

• 线性：\(K(w, z) = z^T w\)(仅解决线性可分问题)

• (2) 多项式：\(K(w,z)= (w^Tz+c)^d\)

• 径向基函数(RBF)：\(K(w, z) = \exp\left(\frac{\|wz\|^2_2}{\sigma^2}\right)\)

• (4) S形曲线：\(K(w,z)=\tanh (\sigma z^2 w + \beta )\)

  训练一个好的SVM分类器总是需要调整正则化系数λ, σ2 （径向基函数）或（\(\sigma, \beta\)（MLP）。在我们的实验中，我们使用带有上述核函数的SVM来建模PUF。对于多项式核函数，我们使用了次数\(d = \left\{ 2,5,10,15 \right\}\)对于整体训练，我们应用了正则化系数\(C=1\).

K均值聚类算法

K均值聚类是将大型数据集分组为不同的独立簇的过程，使得一个簇中的数据对象彼此相似，而与其它簇中的数据对象不相似。³⁷这是一个迭代方法，当达到最优解时终止。在K均值算法中，通过最小化簇内变异性和最大化簇间差异性来实现最优解：\(\sum _{i=0}^{n}\min _{\mu _j \in C}(|x_i - \mu _j|^2)\) 注意：公式中的"||"在数学中通常表示范数（norm），正确的符号应该是单竖线"| |"。所以这里根据数学标准进行了调整，但如果不考虑数学规范，直接翻译的话就是"\(\sum _{i=0}^{n}\min _{\mu _j \in C}(||x_i - \mu _j||^2)\)"，不过通常我们会使用更标准的"| |"来表示范数。原文中可能是一个排版或输入错误。，其中X是样本和μ是不相交的、初始化的簇的手段CK-均值算法在所有样本找到它们最近的聚类中心且不再变化时收敛。μ变得最小或μ不变。对于我们的攻击，我们使用K均值算法和一个称为K均值++的修改变体³⁸修改集群初始化程序以避免由于随机质心放置导致的聚类效果不佳。对于K-means，集群是使用种子值随机初始化的。\(R=0\)对于K-means++，我们使用了种子值\(R=12454\)随意选择的。

高斯混合模型

高斯混合模型（GMM）是由多个高斯分布组成的混合模型³⁹一维高斯分布可以定义为：\(p(x|\mu, \sigma^2) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)\)，其中σ以及μ表示标准差和均值。GMM假设所有数据点都来自有限数量的高斯分布，这些分布的参数是未知的。为了找到这些参数使用了期望最大化算法。具有K高斯成分和权重w由以下方程定义\(\mathcal {N}\left( \mu _{k}, \sigma _{k} \right) = \sum _{k=1}^{K} w_{k} \mathcal {N}\left( x \mid \mu _{k}, \sigma _{k}\right) \quad\)对于我们来说，我们选择的是\(K=2\)作为我们二分类问题的组件数量。

树集成模型

集成模型是由一组较弱的分类器组成，这些分类器通过全局投票或得分聚合规则结合起来以产生更好的预测。对于我们的攻击，我们使用了两种不同的集成模型。第一种是随机森林（RF），这是一种基于决策树组件的集成模型，它由大量的不同决策树共同工作构成一个整体模型。⁴⁰决策树（DT）是一种基于数学树结构的简单分类模型，通过树节点上的决策对样本进行分类。⁴¹叶子节点反过来充当根据设定规则分离的数据容器。各种算法测量分割的不纯度，对于MR-PUF我们使用基尼不纯度。\[Gini = 1 - \sum_{i=0}^{C}(p_i)^{2}\]，其中C表示一个类和\(p_i\)属于某个类别的样本的概率i在给定节点上。杂质越低意味着节点同质性越高， với 由于提供的英文文本中包含未完成的句子或者表达不完整的概念（如"杂质越低意味着节点同质性越高，with" 后面没有继续的内容），直接翻译可能会导致语句不通顺或意义不明。基于指导原则“只输出翻译结果”，我会保持这种形式。但是，如果需要完整、连贯的翻译建议，请提供完整句子以便更准确地传达意思。这里遵循指令仅进行字面对译： 在给定节点上。杂质越低意味着节点同质性越高，with吉尼系数等于0表示节点只包含一个类别（纯节点）。算法中的每棵个体树都会给出一个类别预测，投票最多的预测结果将成为模型的结果。如果\(C_t(x)\)是从树中预测的一个类别的结果t然后从森林中给出全局预测为\(C_F(x) = \text{多数投票}(C_t(x))\)第二种模型是XGBoost（极致梯度提升），它依赖于梯度提升技术，即在这里我们使用梯度增强决策树，这与RF在创建和聚合树木的方式上不同。⁴². 虽然随机森林（RF）同时构建树，但XGBoost依次创建树，并依赖于每个新树创建后的损失函数梯度来改进之前的决策树的不足。此外，XGBoost在创建树的过程中聚合决策，而不是像随机森林那样在最后进行聚合。对于我们的RF模型，我们使用了逐步增加的估计器数量\(N= \left\{ 100,200,400,800, 1600 \right\}\)以及树的最大深度\(D=\left\{5,10,15,25,40\right\}\)对于我们的XGBoost模型，我们使用了相同的设置D对于树的深度和学习率为\(l=0.5\)表格3我们总结了我们的分类器及其超参数。

多层感知器

为了测试我们的PUF的鲁棒性，我们训练并使用了一个通过最近文献显示在攻击中表现出成功的MLP。^27,43,44,45我们的MLP设计用于接受两个输入以预测比特输出。我们实现了浅层和深层的变体以发现最合适的架构。我们的模型由7层组成，包括具有以下深度结构的5个隐藏层：\(2 \Rightarrow 512 \Rightarrow 1024 \Rightarrow 512 \Rightarrow 256 \Rightarrow 64 \Rightarrow 1\)对于我们激活函数的实验，我们在双曲切线之间进行测试\(f(x) = \frac{(e^x - e^{-x})}{(e^x + e^{-x})}\),ReLU\(f(x) = \max(0, x)\)泄漏ReLU\(f(x)=\max(0.01x, x)\)和sigmoid函数\(f(x) = \frac{1}{(1 + e^{-x})}\)最终使用ReLU展示了数值和训练的稳定性。对于最后一层我们使用了sigmoid函数。

长期短期记忆网络

我们希望探索先进的深度学习架构，看看它们是否能够建模MR-PUF。鉴于我们的数据具有每比特仅有两个输入的独特性质，许多分类器无法用于处理这类数据。因此我们将问题重新定义为时间序列预测，其中我们的我以及V值可以被视为一种信号，因此可以按顺序输入到模型中。我们选择了一种改进的循环神经网络变体——长短期记忆网络（LSTM）。循环神经网络是一种能够通过保持内部记忆或状态来处理序列数据的神经网络类型。它设计用于处理长度不同的输入序列，并且可以在时间步骤之间捕获数据中的依赖关系或模式。RNN背后的关键思想是在每个时间步的网络输出成为下一个时间步的输入，从而使其能够在一段时间内维持和传播信息。⁴⁶这个反馈循环使得网络能够处理序列信息，并根据过去的输入上下文进行预测。因此，目标是看看一组对应于位的数据是否会有有助于预测下一个位值的模式。RNN（递归神经网络）在捕捉长期依赖性方面存在局限性，因此我们使用了一种更高级的变体LSTM（长短期记忆网络）。^47,48为了处理这个问题。LSTM通过在每个记忆单元中引入称为门的附加组件来实现这一点。这些门包括输入门、遗忘门和输出门，有助于控制信息流入、流出以及在记忆单元内的流动。遗忘门允许LSTM忘记过去无关的信息，而输入门则允许网络用新的信息更新细胞状态。然后，输出门确定在该时间步使用多少当前细胞状态来生成输出。我们试验了多层感知器（MLP）头部的大小和LSTM层数。LSTM层\(>2\)意味着使用堆叠的LSTM，其中块彼此堆叠，第二个LSTM接收第一个LSTM的输出，依此类推，最后一层计算最终结果。

在本节中，我们将总结评估MR-PUF对前一节展示的机器学习攻击的鲁棒性的结果。使用MATLAB仿真代码提取并测试了MR-PUF输出的随机性预测。我们针对运行攻击框架所进行的时间和内存复杂度分析汇总如下表所示。4使用以下表格中总结的计算基础设施详细信息5值得注意的是，GMM、LR和K-means代表了迄今为止最快的时间复杂度结果，而MLP和LSTM展示了最慢的时间复杂度。在所有情况下，所有模型对于执行的攻击都提供了实际的时间复杂度。对于基于树的模型，我们调整了参数以观察增加模型的复杂性和规模是否能获得更好的结果，然而我们没有发现任何具有统计显著性的性能差异。此外，我们也试验了不同深度学习模型的规模，增加了层数并尝试了不同的激活函数和训练改进方法（如正则化和Dropout）。这些变化也没有带来任何性能提升。对于所有模型，我们报告最佳的ROC曲线和准确率。

完整数据集。

我们进行了数据拆分以产生训练集和测试集。生成的测试集包含总数据集的30%。我们根据最常见的安全级别位数选择了数据集大小。对于我们建模攻击所构建的数据集如图所示。5然后我们对MR-PUF发起了机器学习攻击，分析是在Python中实现的；这些实现基于参考资料中提供的开源库：^51,52,53.

逻辑回归

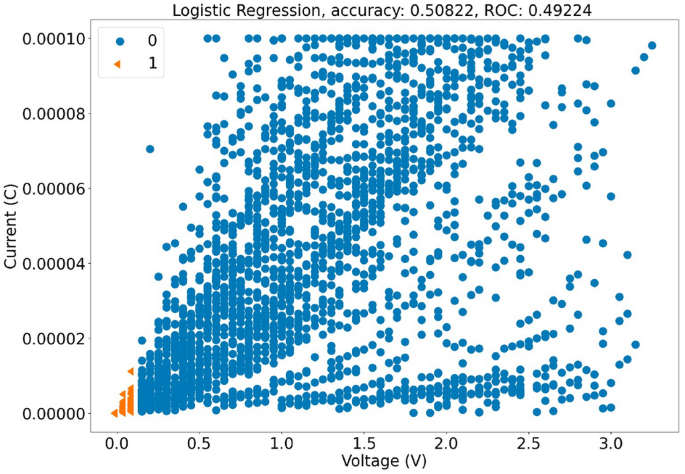
针对PUFs的建模攻击准确率应理想为50%，即对二进制输出进行纯随机猜测。对MR-PUF的LR攻击被评估为具有以下精度：0.508和ROC为0.492如图所示_fig.中的内容请参照具体上下文提供相应的中文表述，此处仅为示例部分的翻译： 如下图所示：6因此，输出位为1或0的概率几乎各占50%，证明了MR-PUF在不使用任何后处理算法的情况下实现了真正的随机性。表中展示了不同PUF（包括MR-PUF）对LR攻击的鲁棒性的比较。1.

逻辑回归（测试集）。

支持向量机与sigmoid核函数（测试集）

支持向量机

对于我们使用的SVM，我们采用了4种不同复杂度级别的核函数。对于所有核函数，我们都使用了\(C=1\)L2正则化参数。对于线性核我们达到了准确率0.517和ROC为0.5，类似的，RBF核函数导致了准确性0.517以及0.5ROC。对于所有次数的多项式核函数\(d = \left\{ 2, 5, 10, 15 \right\}\)我们也达到了准确性0.498和0.501ROC。这些核函数的准确性及ROC相似性是由SVM无法将数据分为两类所导致的。因此分类器将测试集中的所有点都标记为0标签。ROC值为0.5表明该结果是随机的。

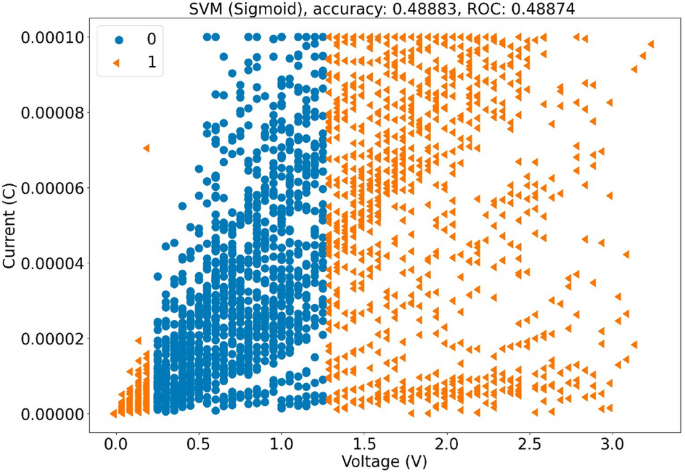
Sigmoid核给出了最佳的聚类视觉分离效果，准确率为0.489和ROC为0.489如图所示Fig. 注意：这里的"as shown in Fig."是常见的英文科技论文或报告中的表达方式，用来指代附带的图表。由于"Fig."已经在中文表述中保留下来，并且“如图所示”已经是这一短语的标准翻译，因此输出结果包含原文中的"Fig."符号。7上面我们展示了sigmoid核的聚类结果。由于我们的数据具有很高的随机性，只有使用sigmoid核的SVM成功将数据分为两个簇，因此我们仅呈现这些聚类结果以减少冗余。

K均值（测试集）

K均值++（测试集）

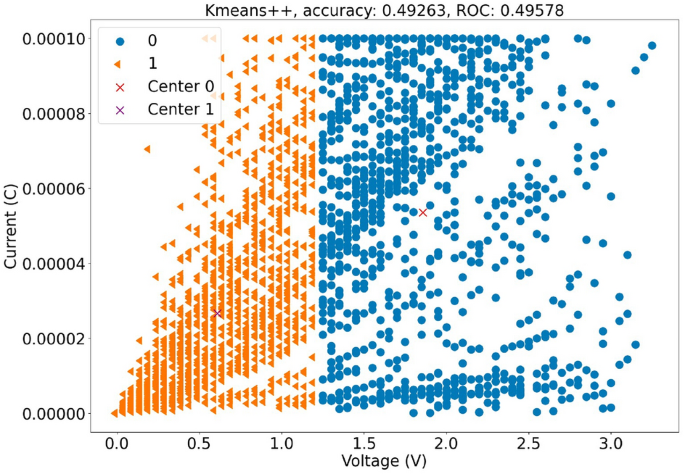
K均值和K均值++

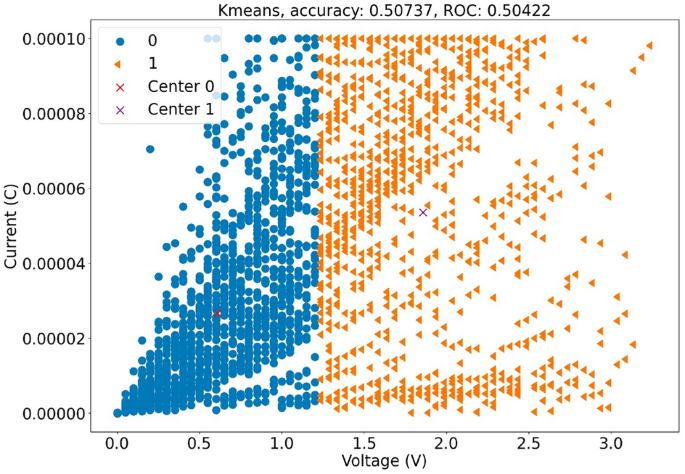
对于K均值和K均值++来说，我们的聚类过程除了初始化步骤之外是相同的。K均值的准确率为0.507和ROC为0.504如图所示fig. 注意：这里的“as shown in Fig.”是常见的英文科技论文中的表达方式，翻译为中文时通常使用“如图所示”，后面跟具体的图编号（例如：“如图1所示”）。由于原文中没有给出具体编号，因此保留了“fig”。如果需要更正或添加具体编号，请提供进一步信息。不过根据指示仅输出翻译内容且无实际内容需要修改时输出原文，所以此处按照要求处理。8而K-means++达到了准确性为0.493和ROC为0.496如图所示(fig.)9两个聚类算法都没有很好地分离数据，并且K-means++返回的聚类结果与K-means相同，但标签相反。

高斯混合模型（测试集）。

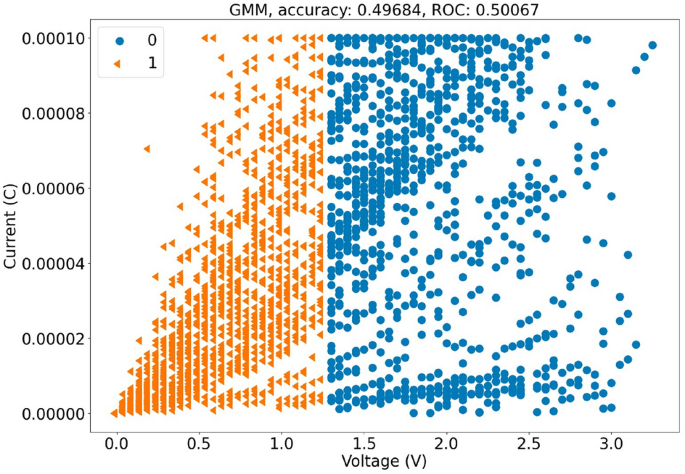
高斯混合模型

我们选择了\(K=2\)作为高斯混合模型的组件数量。我们的攻击达到了0.497准确性与0.501ROC。虽然与K-means和K-means++相比，GMM通常被认为是一种更强大的聚类算法，具有较软的概率边界，但它未能正确区分标签，进一步证明了MR-PUF的随机性。结果如下图所示。10.

多层感知器（测试集）。

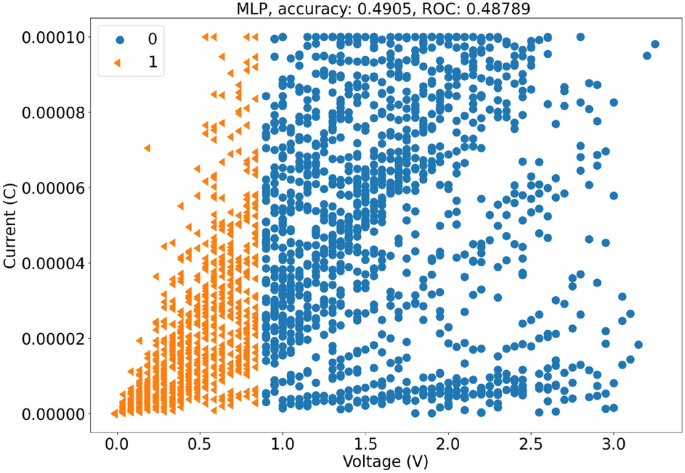
多层感知器

回想一下，我们的人工神经网络（ANN）结构如下：7层，维度分别为：\(2 \Rightarrow 512 \Rightarrow 1024 \Rightarrow 512 \Rightarrow 256 \Rightarrow 64 \Rightarrow 1\)，除了最后一层之外的所有层都使用了ReLU激活函数，最后一层使用了Sigmoid激活函数。该模型在学习率为0.0005的情况下训练了1000个周期，使用Adam优化器和BCE损失函数。此外，在最终达到数值稳定版本之前，我们尝试了多种架构，并且该稳定版本在训练和验证过程中始终表现出损失下降的趋势。我们在图中展示了我们的结果。11在这里我们可以注意到，ANN未能准确预测数据集中的样本，即它的准确性为0.491和ROC为0.488

长短期记忆网络

对于我们的LSTM，我们同时测试了堆叠版本和非堆叠版本，并且改变了MLP头部的大小。我们观察到增加LSTM堆栈不会提高准确率。MLP头部结构使用ReLU激活函数，输出层使用sigmoid激活函数。\(LSTM \Rightarrow \textit{隐藏大小} * 2 \Rightarrow 256 \Rightarrow 128 \Rightarrow 1\)增加MLP的大小也没有影响最终的准确性。模型使用学习率为0.0001、Adam优化器、BCE损失函数和批次大小为5的情况下训练了30个周期。我们在训练和验证过程中也观察到轻微但稳定的损失减少，尽管如此，我们达到了准确率的0.517和ROC（接收者操作特性） của0.5一个模型常常会失败，无法做出分离边界，导致整个数据集要么被标记为0，要么被标记为1。

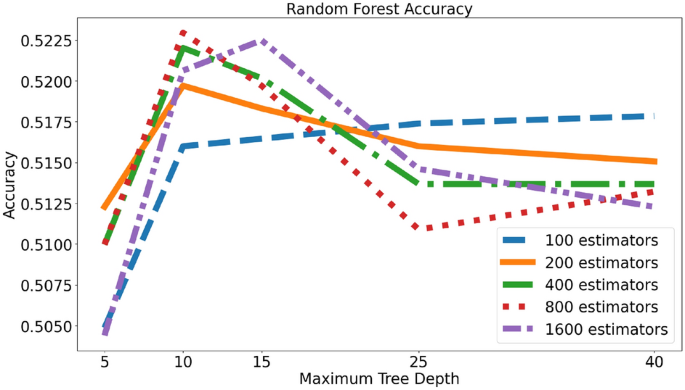
随机森林

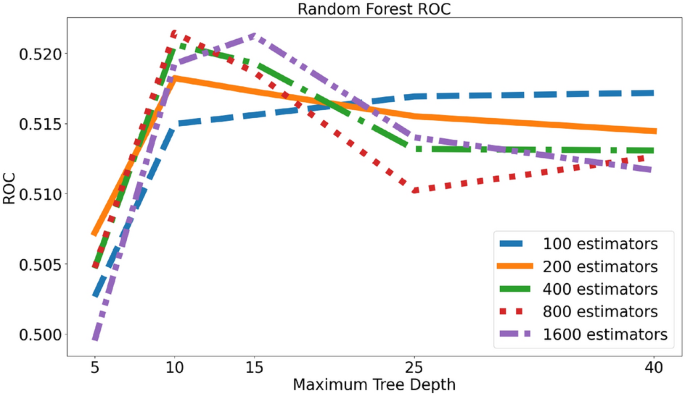
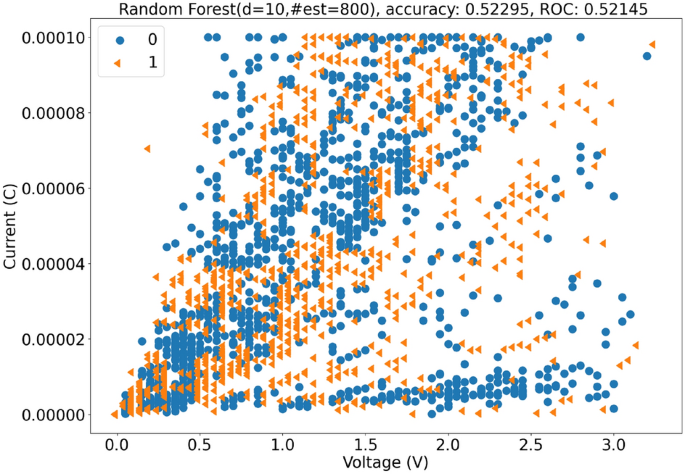
我们的随机森林设置包括一个超参数搜索，以找到最佳的估计器数量和树的最大深度。我们将在下面的图中提供不同配置在准确率和ROC方面的比较。12以及13分别而言。值得注意的是，包含更多估计器和树深度的分类器构建时间更长，但不一定能提供最佳结果。我们还提供了最佳配置（最大深度=10，估计器数量=800），准确率为0.523和ROC（接收者操作特征） của0.522见图所示。14以下。

随机森林准确率（测试集）。

随机森林ROC（测试集）。

随机森林最佳结果（测试集）。

XGBoost准确率（测试集）。

XGBoost ROC（测试集）

XGBoost最佳结果（测试集）。

XGBoost

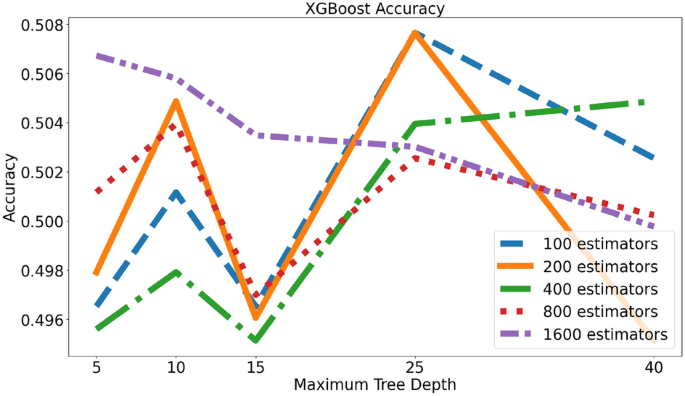
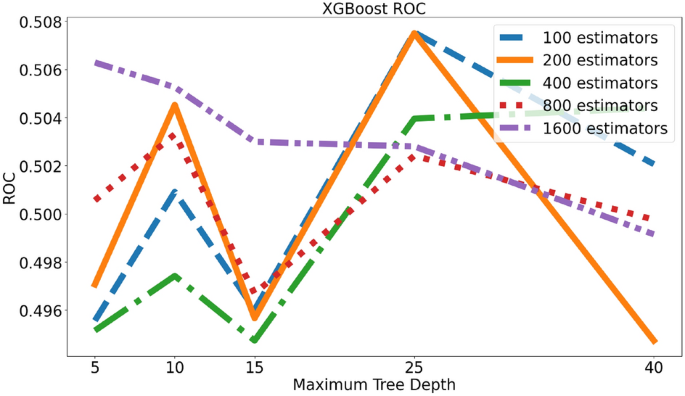
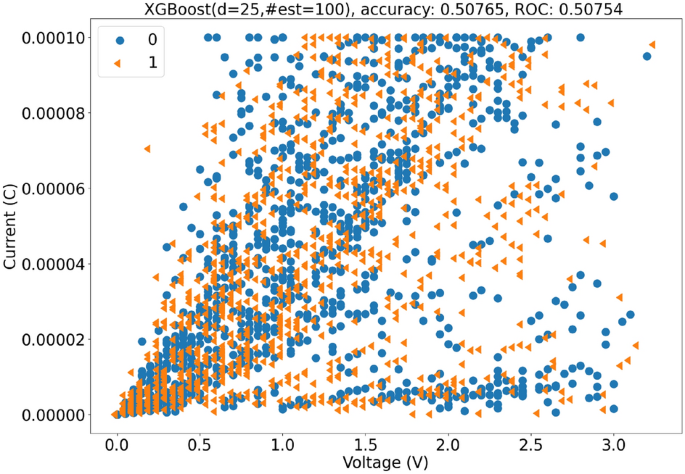
对于我们使用的XGBoost模型，我们选择了一个与随机森林类似的设置，以便对两者进行全面比较。具体来说，我们使用了相同的估计器集E和深度集D来构建我们的模型。所有配置的准确率和ROC结果如图所示。15以及16分别而言。与RF相比，XGBoost得益于更大的树深度。我们最好的XGBoost分类器（最大深度=25，估计值数量=100）实现了的准确率为0.508和ROC（接收者操作特性）曲线的0.508我们在图中展示了它的分类结果。17.

作者和 affiliation（机构信息）

1. EMARATSEC，阿布扎比纽约大学，萨迪亚特岛，阿布扎比，阿拉伯联合酋长国 129188

   海贝塔拉赫·M·伊布拉希姆，乔治·斯科沃罗迪诺夫，霍达·阿尔赫宰米

贡献

H.I.撰写论文并构建了忆阻器框架。H.I.从MR-PUF收集数据集并评估随机性。H.I., H.S和H.A设计了用于研究的机器学习分析工具。H.I.和H.S进行了机器学习分析。H.A监督了研究。所有作者审阅了论文。

通讯作者

通信地址为 海巴塔拉赫·M·伊布拉希姆.

利益冲突

作者声明没有利益冲突。

出版者注释

施普林格·自然对于出版地图和机构隶属关系中的管辖权主张保持中立。

开放访问本文根据知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议发布。在遵守该协议条款的前提下，允许任何非商业用途、分享、分发和复制，无论任何形式或媒介，只要您给予原作者适当署名，并提供知识共享许可链接，以及表明是否对授权材料进行了修改。在此许可下，您没有权限分享基于本文或其部分内容的改编作品。除非另有说明，在该信用线中声明，本文中的图片或其他第三方材料均包含在本文的知识共享许可证内。如果材料未包括在本文的知识共享许可证中，并且您的预期用途不被法律规定允许或者超出允许范围，则需要直接从版权持有人处获得许可。欲查看此许可证副本，请访问http://creativecommons.org/licenses/by-nc-nd/4.0/.

重印和许可