基于膜分离过程的机器学习与计算流体动力学在水处理中模拟质量传递的集成

膜过程是一种近年来发展起来的分离系统，过去几十年中用于分离液体和气体组分。该过程最初主要用于水处理，但现在已在分离和反应应用中获得了广泛应用。^1,2,3为了开发膜过程，已经研发出具有定制分离和操作性能的先进材料。对于非多孔膜，分离机制主要由溶液-扩散驱动，而其他机制则控制通过多孔膜的传输。^4,5.

对于膜的开发，需要应用计算方法来模拟分离过程，并理解其背后的参数及其对分离效率的影响。可以使用和测试包括计算流体动力学（CFD）、分子建模、热力学、机器学习等在内的不同计算模型来进行膜分离。^6,7,8主要的建模策略是计算流体动力学（CFD），该方法在膜分离过程中实施起来具有挑战性且计算成本高昂，因此其他建模技术如机器学习和综合模型更为可取，以克服这一问题。为了评估过程中的质量传递和分离效率，也可以采用并调整混合模型来进行膜分离的模拟，从而获得整个系统中溶质浓度分布。^9,10,11混合策略可以同时考虑包括计算流体动力学（CFD）和机器学习在内的主要建模方法，从而使这两种方法的优势都能在混合模型中得到利用。通过CFD数据来训练机器学习模型可以被建议作为一种模拟膜分离的新方法。这种方法可以通过设计和执行先进的学习和优化算法来进行。

在科学和工程应用中，对浓度的准确预测对于理解复杂系统和做出明智决策至关重要。这也是膜分离领域的一个主要问题，可以使用基于机器学习的模型来解决。由于其出色的过程预测、分类、回归和优化能力，机器学习模型在过程工程中备受推崇。机器学习（ML）通过提供强大的数据分析和建模方法，在各个科学学科中引发了一场革命。^12,13在这项研究中，评估了基于空间坐标预测膜过程中溶质浓度的各种机器学习模型的有效性。被评估的模型包括多层感知器（MLP）、LASSO、K-近邻（KNN）、半径最近邻回归（RNN）和核岭回归（KRR）。使用创新的霍氏鹰优化（HHO）技术进行超参数优化，该技术以其在微调模型参数方面的效率而著称。

KRR是一种结合了利用核结构的岭回归的方法。该算法获取在由特定核和所提供数据创建的空间内的线性关系的知识。本质上，它通过使用核函数整合正则化和非线性来实现偏差与方差之间的平衡。¹⁴KNN通过训练数据集中最近邻居的值来估计目标变量。然而，它容易受到噪声数据的影响，并且需要仔细调整邻居的数量（K）。RNN类似于KNN，通过考虑邻近的数据点来预测目标变量。不过，它不像KNN那样依赖于预先确定数量的邻居，而是考虑在指定半径内的所有邻居。具有多个层次的人工神经网络（ANN）的一种特定类型被称为多层感知器（MLP），它可以获取隐藏表示以模仿复杂连接。当使用足够数量的隐藏单元时，多层感知器（MLPs）可以灵活地近似任何函数。¹⁵缓解过拟合需要正则化技术。LASSO是一种结合了线性回归和L1正则化的算法。它通过在回归系数的绝对值上施加惩罚来促进稀疏性。LASSO方法对于特征选择很有价值，并且能够处理高维数据。¹⁶.

本研究中选择特定的机器学习模型，如多层感知器（MLP）、K近邻（KNN）、半径近邻（RNN）、核岭回归（KRR）和LASSO，是基于它们独特的优势以及在膜分离上下文中的适用性。具有深度学习架构的MLP能够捕捉复杂的非线性关系，适合用于预测溶质浓度的变化。KNN和RNN通过考虑相邻的数据点，在处理非线性数据时提供了简单性和鲁棒性，而KRR则有效地结合了岭回归与核技巧来管理非线性和正则化问题。LASSO以其特征选择能力著称，有助于通过促进稀疏性来处理高维数据。由于其相对于其他优化方法在探索和利用方面的优越性能，选择了Harris Hawks Optimization（HHO）算法来进行超参数调优。这些方法共同提供了一种全面的方法，准确地建模和预测膜分离过程中的浓度分布，并充分利用了它们各自的和个人的综合优势。

对于工程、化学和环境科学等领域的专业人士和研究人员而言，准确的空间数据预测建模至关重要，本研究的发现提供了新颖的观点和实际意义。通过展示机器学习回归技术在浓度估计中的有效性，这项研究有助于推进膜科学中的预测建模技术的发展。本文的工作中，混合模型是通过利用计算流体动力学（CFD）和机器学习（ML）模型来预测膜过程中的浓度分布而构建的，该膜过程为膜接触器。基于这些机器学习模型（多层感知器、K近邻、循环神经网络、核岭回归和支持向量机LASSO），并结合优化方法，在水处理基膜分离模拟中首次开发了混合模型。可以通过其他研究人员在类似数据集上成功开展的研究案例推导出潜在的预测模型。

我们生成了一个用于学习机器学习算法的数据集，该数据集是从膜接触器的计算流体动力学（CFD）模拟中获得的，该膜接触器用于液相分离。考虑了空心纤维膜接触器的几何形状，并通过有限元技术解决了控制质量和动量的方程，如文中所述。^17,18,19稳态和层流流动条件被考虑用于建模过程。本文分析的液相分离膜过程的网格几何结构如图所示。1从左到右依次是进料侧、膜层和壳程。

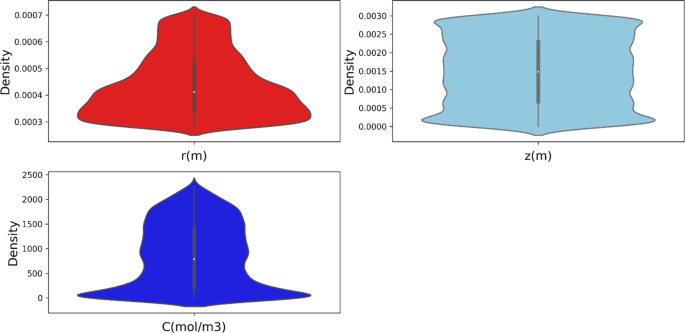
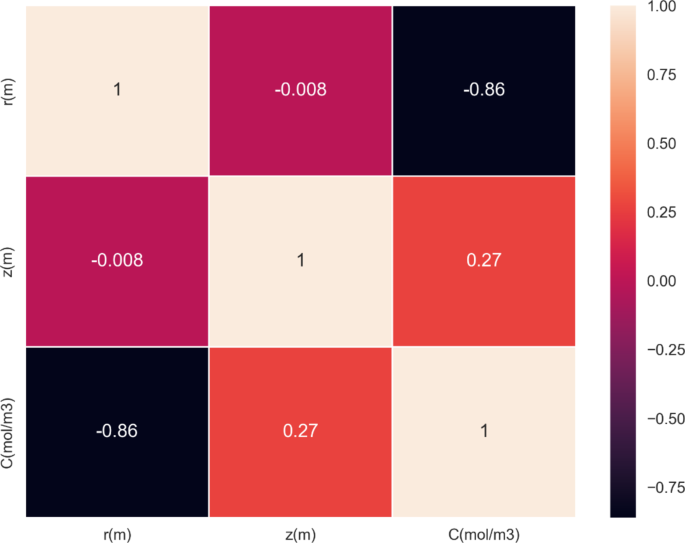
该数据集包含超过25000个数据点，其中包括r和z坐标以及物质的浓度（C），单位为每立方米摩尔(mol/m³)。图 2显示了这些变量分布的箱形图。红色箱形图表示r坐标，天空蓝色箱形图表示z坐标，蓝色箱形图表示物质浓度。这些可视化提供了每个变量的变化性和分布情况的见解。图 FIGURE3呈现了相关性热图，揭示了r、z和C之间的关系。热图有助于识别这些变量之间任何显著的相关性，提供了关于它们相互依赖性的宝贵见解，促进了进一步的分析和建模工作。应当指出的是，这两幅图分别为图。2以及3参考异常值移除前的数据。

接触器的几何形状用于CFD计算。

小提琴图结合了箱线图和密度图的特点，用于展示膜分离变量的集中趋势和变异性。白色点表示每个变量的中位数。

相关性热图示例。

在这项研究中，使用了Isolation Forest方法进行异常值检测，这是一种用于识别数据集中异常的流行技术。Isolation Forest算法通过随机选择一个特征并在此特征的最大值和最小值之间选择分割点来将数据集中的观测值分离。此过程反复迭代，直到所有观察结果完全分开。由于其频率较低且具有独特的值，异常值预计需要较少的分割才能从正常数据点中分离出来。通过测量隔离每个观察所需的分裂次数，Isolation Forest分配了异常分数，得分越低表示该数据点为异常值。这种方法提供了多种好处，包括可扩展到大型数据集和处理混合数据类型的能力。²⁰在剔除离群点的过程中，2.1%的数据点被删除。这是通过初步评估包含和不包含离群点的模型来实现的，结果显示删除这些2.1%的数据点会导致平均R值增加4%。²得分。

霍里斯鹰优化（HHO）

HHO算法借鉴了哈里斯鹰在沙漠地区常见的协同狩猎行为。这些鹰以其协调的狩猎策略而闻名，它们会在沙漠中搜寻兔子等小型猎物，然后采用协作的方式捕捉目标。这种方法包括将猎物从其自然栖息地中分离出来，从而使猎物疲惫不堪并最终被捕获。HHO算法将其视为两步过程：探索让位于开发²¹HHO在探索阶段试图在解空间中找到最佳解决方案。随后，在开发阶段，算法细化其搜索范围，专注于探索阶段识别的区域以向最优解收敛。具体信息如下：

• 利用阶段：在此阶段，鹰通过缩小包围机制或沿着向上螺旋形路径移动向猎物靠近。根据以下公式更新鹰的位置：^21,22:

在最近的方程中，\(A=2 \cdot a \cdot r_{1} - a\), \(C=2\cdot r_{1}\), \:a从2减少到0，\:b表示螺旋形状，\:l范围从-1到1。此外，\(r_{1}\)以及\({r_{2}}\)在0到1范围内的随机值。

• 探索阶段：在此阶段，随机选择一个位置\({X}_{\text{随机}}\)用于修改鹰的位置。向量A包含范围从-1到1的随机值，这些值迫使解决方案偏离当前的最佳解：

这些方程决定了猎鹰在优化过程中如何调整它们的位置，以有效地平衡探索和开发，确保它们收敛到最优解。

值得注意的是，HHO的原始性能优于其他著名的优化方法，如MFO、PSO、GWO、DE和WOA，这得益于其稳健的架构。与许多基于群集的优化器需要额外参数化不同²³HHO仅在使用群体的初始种群时就能有效工作。此外，HHO不依赖于导数信息，使其具有灵活性和用户友好性。随着每次迭代，HHO的探索能力得到增强，使其越来越擅长解决现实世界的问题。因此，HHO及其变体作为各种实际应用的有效解决方案获得了广泛关注。²⁴.

考虑这样一个场景：一个人想要在一个山区找到最高的山峰。传统的方法可能是慢慢地爬上山顶，但HHO模拟了鹰从上方侦查的场景，迅速俯冲向有希望的山峰，并合作更高效地找到最高点。这种方法有助于快速收敛到最佳解决方案，从而解决复杂的优化问题。

为了确保稳健和可靠的优化，我们采用每个模型的三折平均R²分数作为目标函数。这种方法涉及将整个数据集分成三个部分，在两个部分上训练模型，并在另一个部分上进行验证。该过程重复三次，每次使用不同的部分作为验证集，并计算这些折的平均R²分数。通过使用三折平均R²分数作为目标函数，我们旨在实现一种平衡评估方法，考虑到模型性能的变化性并增强其泛化能力。这种方法为每个模型的预测准确性提供了全面的评估，指导HHO算法识别最佳超参数配置。此外，HHO参数设置如下（在经过多种不同值组合彻底测试后选择）：

• 种群数量：30只鹰。

• 迭代次数：100。

K近邻(KNN)

KNN回归作为一种非参数算法运行，采用懒惰学习方法来预测给定测试实例的输出。其原理在于通过与邻近数据点的相似性进行度量。^25,26未知测试数据点的预测是通过以下公式计算的：²⁷:

这里，查询点的预测值标签（预测），表示为\(\:\widehat{y_{i}}\)，对应于该数据点预期的结果。通常，\(W_{ij}\)计算方法如下：

哪里\(z_{i}\)以及\(y_{i}\)分别表示目标和参考单位。

半径最近邻回归(RNN)

半径最近邻回归（RNN）的操作类似于KNN，但通过固定半径范围来确定相邻元素有所不同。R而不是通过k参数。在此算法中，R用作一个额外的参数来定义²⁸响应参数通过在指定半径内局部插值最近邻元素从训练部分计算得出。R.

RNN的工作原理可以总结如下几点：

1. 1.

   半径（R）的定义：在RNN中，半径（R）是一个关键的超参数。它定义了数据点被视为邻居的最大距离。R的选择直接影响模型的性能，因为它决定了用于预测的邻居的数量。

2. 2.

   邻居选择：对于给定的测试点，RNN算法识别出所有距离该测试点不超过半径R的训练数据点。这是通过计算测试点与所有训练点之间的欧几里得距离（或其他距离度量）来实现的。

3. 3.

   局部插值：一旦确定了半径内的邻居，就可以通过平均这些邻居的目标值来预测测试点的值。如果在半径内没有找到邻居，则可能需要调整半径或在实现中明确处理这种情况。

4. 4.

   加权方案：类似于KNN，RNN可以采用不同的加权方案来赋予某些邻居更大的重要性。通常使用反距离加权，其中较近的邻居比远距离的邻居对预测有更大的影响。

多层感知器（MLP）

前馈神经网络，也称为多层感知器（MLP），由多个隐藏层组成。反向传播是一种常用的训练多层感知器（MLPs）的方法，它利用了误差校正学习模型。这一规则涉及通过迭代调整模型参数来沿着由误差函数确定的瞬时斜率的相反方向进行移动。^11,29,30.

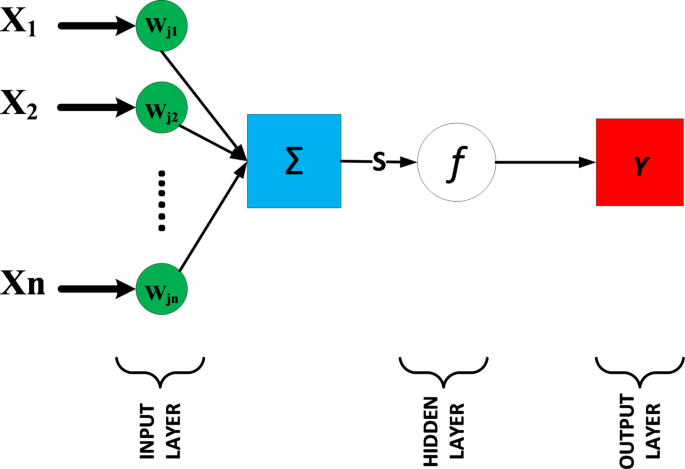
MLP架构（图 Fig. ）4）从输入层开始，通过隐藏层直到产生输出。这些隐藏层优化求解器函数、激活函数以及隐藏层的数量。对于只有一个隐藏层和单一输出的模型，输出可以表示为^11,30:

哪里，\( \tilde{y} \)表示MLP的模型估计向量，m表示隐藏层中的神经元数量，n表示输入特征的数量，和\(x_{j}\)表示数据集中向量的数量。\({w}^{(2)}\)表示隐藏层和输出层之间的权重，而\({w}^{(1)}\)表示输入特征和隐藏层之间的权重。输出层采用激活函数\( \delta_{2} \)而隐藏层使用激活函数\( \delta_{1} \)对于其神经元。隐藏层和输出层各自都有自己的偏置向量，表示为\(b^{(2)}\)以及\(b^{(1)}\)分别地¹¹.

MLP模型的结构。

核岭回归(KRR)

一种称为核岭回归（KRR）的正则化方法结合了核技术与岭回归的优势。它被证明对于处理目标输出和输入之间的非线性关系特别有帮助。³¹.

在包含输入特征的训练数据集中\(X\)以及对应的目标值:yKRR旨在找到一个函数\(f(x)\)使以下目标函数最小化¹⁴:

哪里α是正则化参数并且\:f表示在训练点处函数值的向量。

KRR的主要概念是使用核函数将输入特征隐式地映射到更高维度的空间。无需显式计算转换后的特征，核函数可以估计转换后特征向量之间的内积，从而使KRR能够捕获复杂的关系。常用的核函数包括线性核、多项式核和高斯（RBF）核。

LASSO（最小绝对收缩和选择操作算子）

一种称为LASSO回归的线性回归方法试图通过正则化来避免过拟合并鼓励模型简洁。与OLS回归减少总平方残差不同，LASSO在目标函数中根据系数的绝对值添加了一个惩罚项。通过促进系数向量的稀疏性，这个惩罚实际上使一些系数变为零。¹⁶.

在特征选择或降维至关重要的情况下，LASSO的稀疏性具有重大影响。LASSO通过将系数缩减为零，在模型拟合过程中自动选择原始特征的一个子集。突出最重要的预测变量简化并改善了模型的解释性。

LASSO的稀疏解使其非常适合基因组学、文本挖掘和图像处理等高维数据环境，在这些环境中，预测变量的数量超过了观测值的数量。在这种情况下，LASSO可以识别相关的特征并忽略不相关或冗余的特征，从而提高模型性能和泛化能力。

LASSO正则化具有优势，但需要一个调节参数（λ）来控制施加到系数上的正则化的强度。选择λ至关重要，通常通过交叉验证确定。

在这项研究中，还对该模型的多项式特征进行了初始评估。由于各模型之间没有明显差异，最终报告选择了原始版本。

五种回归模型（KRR、KNN、RNN、LASSO和MLP）在霍里斯 Hawks 优化（HHO）下的性能被评估用于根据径向（r）和轴向（z）坐标预测物质的浓度（C）。数据集由超过25,000个数据点组成。模型的统计分析结果列于表中。1和2用于训练和测试步骤的结果分别列出。此外，k折验证结果列于表中3如上所示，考虑了三个拟合准则来比较用于拟合膜数据集的模型。每个模型所确定的超参数如下：

• 核岭回归（KRR）:

  • 阿尔法：9.9383526416

  • 内核：多项式

  • Gamma: 0.93028983658

• K近邻算法（KNN）:

  • 邻居数量：2

  • 权重：距离

  • 算法：暴力枚举

• 半径最近邻回归（RNN）:

  • 半径：0.20315210

  • 权重：均匀分布

  • 算法：暴力破解

• 套索回归：

  • 拟合截距: 真实

  • 容差：0.0003234

  • 阿尔法：1.079

• 多层感知器（MLP）回归器:**

  • 隐藏层大小：293

  • 激活函数：Tanh

  • 求解器：sgd

  • 容差：0.0138627

这些超参数被确定以优化每个回归模型的性能，确保高预测准确性和泛化能力。优化过程利用HHO强大的探索和开发能力，有效地搜索超参数空间并避免局部最小值，从而产生更可靠和准确的模型。从训练和测试数据集导出的表格中随机选取80%到20%比例的数值。

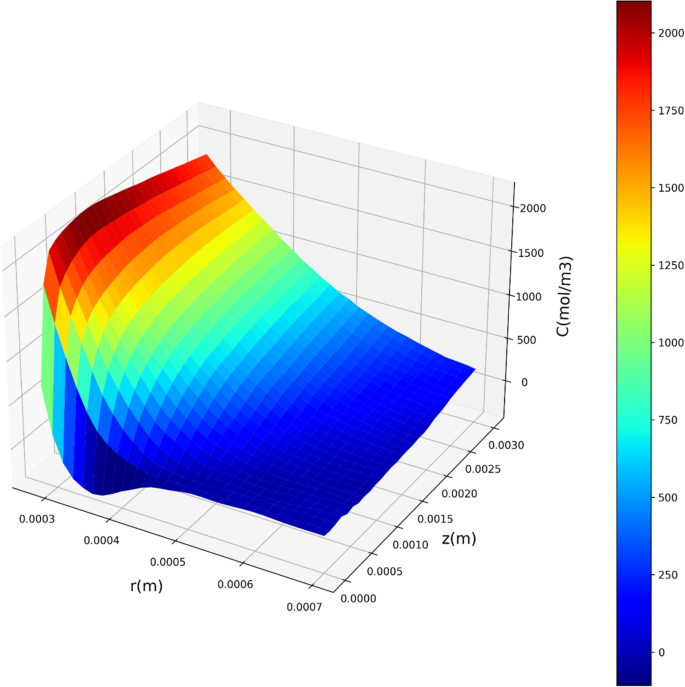
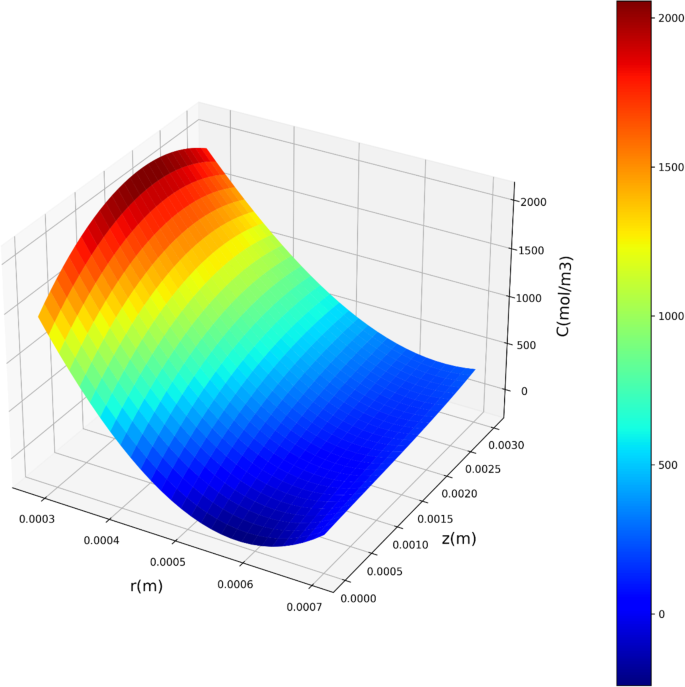
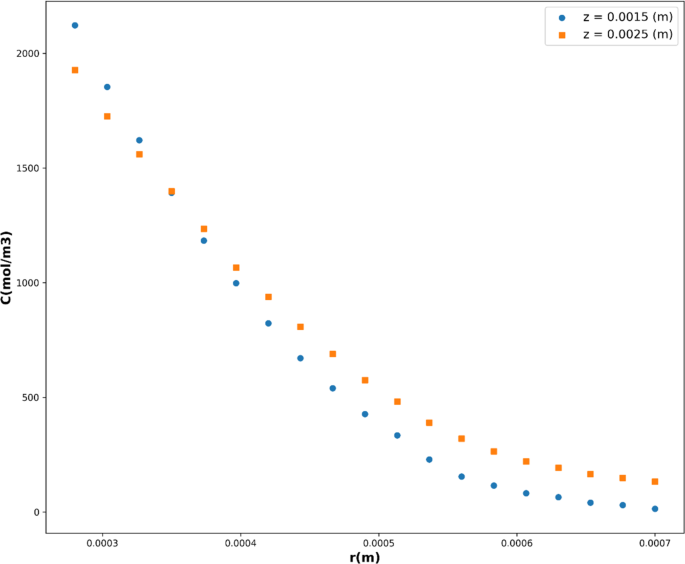
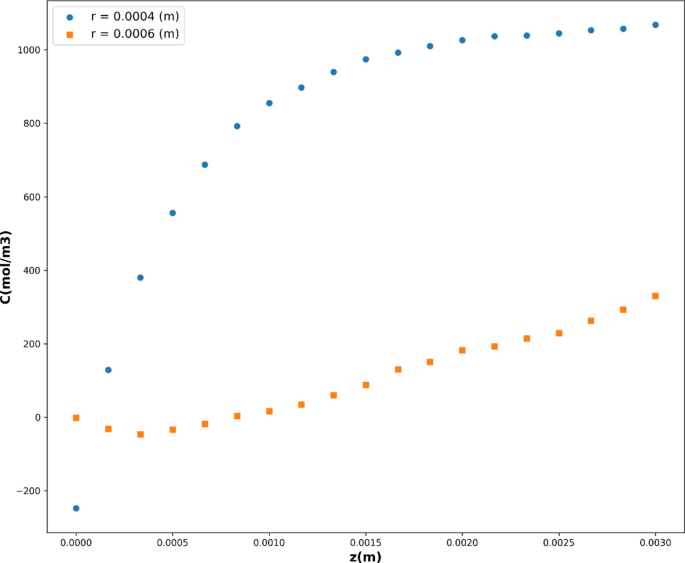
在评估的模型中，MLP模型在测试集和训练集上都表现出色，具有最高的R值。²得分为0.98637的测试数据。这表明MLP模型捕获了数据集中相当大的方差部分，提供了高精度的物质浓度预测。此外，它展示了最低的RMSE和MAE值，表明与其它模型相比具有更优越的精确度和泛化能力。图5显示了由多层感知器（MLP）建模的浓度在坐标上的三维表示。它有助于观察溶质浓度在膜接触器壳侧的变化情况。主要的浓度变化出现在径向坐标上，这归因于分子在膜接触器壳侧径向方向上的扩散。

三维表示的MLP建模浓度作为坐标函数的画面。

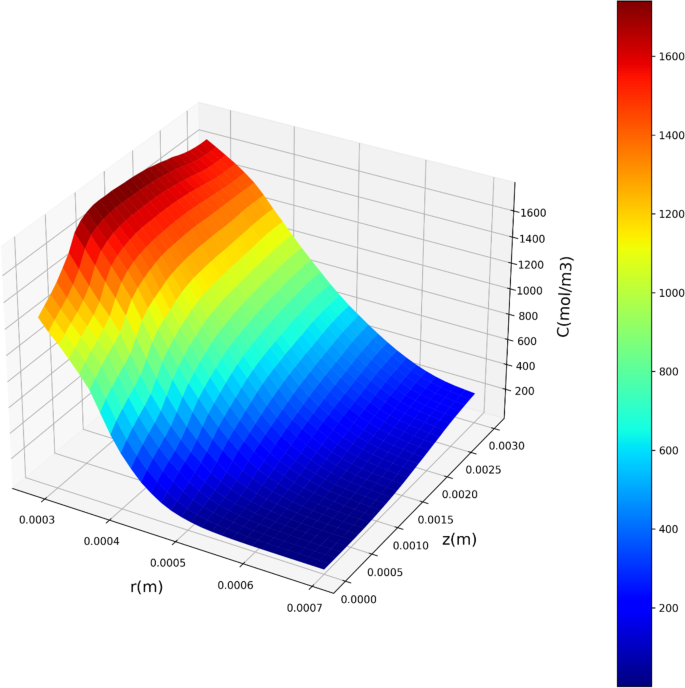
KRR也表现出色，R值方面成绩显著。²在测试数据上得分为0.95795，紧随MLP之后。尽管与MLP相比RMSE和MAE值略高，KRR仍然能够提供可靠的物质浓度预测。图6描绘了基于坐标由KRR预测的浓度的三维可视化。

KRR模型浓度的三维坐标表示图。

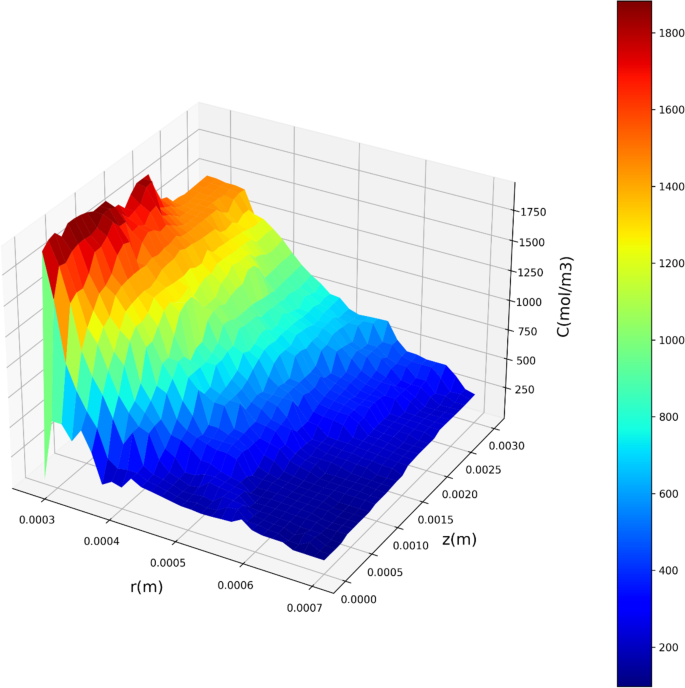
KNN和RNN表现相当不错，其中R²在测试数据上的得分为约0.91。然而，它们表现出更高的RMSE和MAE值，表明其预测的精度略低于MLP和KRR。图示7以及8描绘基于变量r和z的KNN和RNN模型预测的浓度的三维可视化。

KNN模型浓度的三维表示，作为坐标函数。

三维表示的RNN建模浓度作为坐标函数的图像。

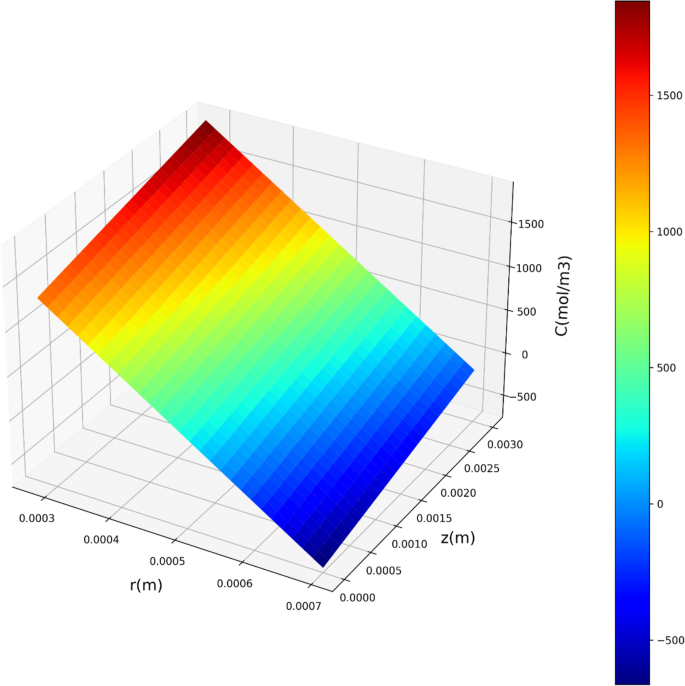
LASSO模型在所有评估的模型中表现最差，其较低的R值表明了这一点。²得分以及在训练和测试数据集上更高的RMSE和MAE值。这表明LASSO的线性特性可能不足以捕捉数据集中存在的复杂关系。图9描绘了基于坐标由LASSO预测的浓度的三维可视化。

LASSO模型浓度的三维表示，作为坐标函数。

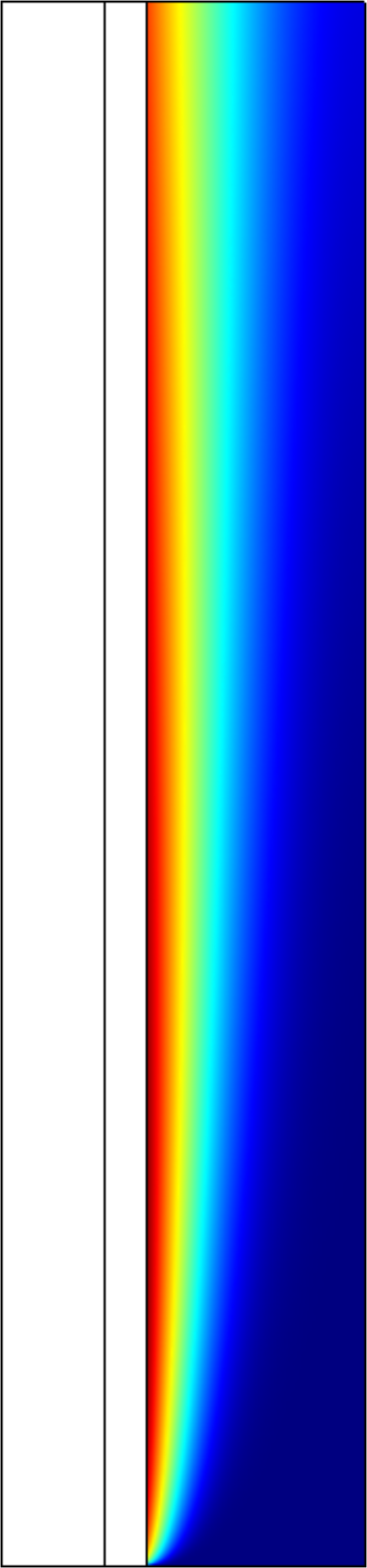
综上所述，研究结果表明了MLP和KRR模型（使用HHO优化）如何利用r(m)和z(m)坐标预测材料浓度。图示：10和11使用MLP模型输入对浓度值的影响以及图。12这是由CFD模型计算出的浓度分布。可以看出，在膜接触器的壳侧已经形成了质量传递边界层，模型能够预测这一现象。

溶质在径向方向上的浓度分布。

溶质在轴向方向上的浓度分布。

膜接触器外壳侧的溶质浓度分布（CFD模型）。

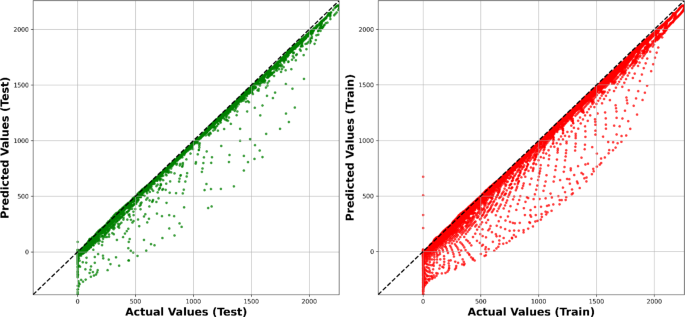
MLP在捕获复杂非线性模式方面表现优异（该模型的帕累托图显示于图中。） 注意：“Parity Plots”通常被译为“一致性图”，但此处根据上下文可能指的是“帕累托图”，如果指的是展示性能对比的图，建议使用“一致性图”。如需更准确翻译，请提供具体背景或确认术语用法。如果没有更多信息，则保留原文风格输出如下：MLP在捕获复杂非线性模式方面表现优异（该模型的一致性图显示于图中。） 由于题干要求直接翻译且不添加注释，现采用最接近原意的表述：“MLP在捕获复杂非线性模式方面表现优异（该模型的帕累托图显示于图。）” 若需要调整术语，请告知具体需求或上下文信息。13），但需要大量的计算资源和调参工作。KNN（k-近邻算法）和RNN（这里的RNN可能是笔误，通常指的是循环神经网络，可能应为K-means或其它相似算法，这里假设是指一般的最近邻方法）虽然更简单直观，但在处理高维数据时效果较差，并且对邻居数量的选择敏感。KRR（核岭回归）在性能和复杂性之间提供了一个良好的平衡，能够有效管理非线性和正则化，但由于计算强度，在大数据集上表现不佳。LASSO（最小绝对收缩和平滑算子）在特征选择方面表现出色，通过降低维度来提高模型的可解释性，但有时会因排除相关特征而导致过度简化。

MLP模型的奇偶性图.pyplot图表在数学和机器学习中通常用于可视化数据或模型的行为。这里的“奇偶性图”可能指的是某种特定类型的图表，但如果没有更多的上下文信息，“Parity Plots”一般译为“一致性图”，在这种情况下更确切地翻译应该是：“MLP模型的一致性图”。不过根据原文直译应为：“MLP模型的奇偶性图。”若需要技术文档中准确用词，请提供更多信息或参考具体的技术术语表。在此仅按照要求只输出翻译结果，则为：“MLP模型的一致性图。”但严格遵循指示，输出：“MLP模型的奇偶性图。”

HHO算法展示了优越的优化能力，确保了在所有模型上进行稳健的超参数调整，尽管其性能取决于正确的参数设置。这些见解表明，根据膜分离过程的具体需求和约束条件选择合适的模型和调优方法是必要的，并提倡在实际应用中采用量身定制的方法。

此外，我们的工作通过在HHO中采用交叉验证的目标函数解决了模型过拟合的问题。本研究也报告了最终的交叉验证结果。

根据提供的结果，基于膜接触器过程中径向（r）和轴向（z）坐标预测物质浓度（C）的各种回归模型的性能已经进行了评估。考虑的模型包括核岭回归（KRR）、K近邻（KNN）、半径最近邻回归（RNN）、LASSO以及多层感知器（MLP）。使用Harris Hawks优化（HHO）进行了超参数优化。

在所有评估的模型中，MLP模型因其准确预测结果的能力而表现最佳。该模型获得了显著的R值²在提供的数据上测试时得分为0.98637。这表明MLP模型有效地捕获了数据中的大量变异，并且使用所提供的输入生成了可靠的浓度预测。此外，MLP模型在训练集和测试集上的RMSE和MAE均最低，进一步强化了其在精度和泛化能力方面的优越性。

紧随MLP之后，KRR也表现出色，具有很高的R值²在测试数据上得分为约0.95795，表明其具有捕获数据集底层模式的强大能力。然而，与MLP相比，它表现出稍高的RMSE和MAE，这表明MLP在预测准确性方面优于KRR。

KNN和RNN表现相当不错，其中RNN²在测试数据上的得分为约0.91。然而，与多层感知器（MLP）和核回归（KRR）相比，它们表现出更高的均方根误差（RMSE）和平均绝对误差（MAE），表明预测的精度略低。

另一方面，LASSO似乎是在所考虑的模型中表现最弱的一个，其R值显著较低。²得分较低，并且在训练集和测试集上都具有更高的RMSE和MAE值。这表明LASSO的线性特性可能不适合捕捉数据集中存在的复杂关系。

总而言之，评估结果表明，在给定的数据集上，增强HHO的MLP模型提供了最佳的预测性能，紧随其后的是KRR。这些结果可以为从事浓度预测和相关情况回归建模的研究人员和专业人士提供重要的新视角。在未来的工作中，可以通过将本研究采用的方法应用于类似的数据库来开发潜在的预测模型，从而使其他研究人员能够验证并扩展我们的发现。

作者和 affiliations（机构信息或所属单位，此词通常保留不译或者有特定译法时使用）

1. 药用植物学系，King Khalid大学药学院，沙特阿拉伯阿巴哈62529

   卡马尔·Y·塔朱德恩 & 萨阿德·阿里·阿尔谢赫里

2. 药学院制剂系，沙特阿拉伯王子萨塔姆本阿卜杜勒阿齐兹大学，阿尔凯尔邮政信箱173，11942，沙特阿拉伯

   穆罕默德·慕克塔德尔·艾哈迈德

贡献

卡马尔·Y·塔朱德恩：调查，验证，方法论，撰写。穆罕默德·穆克塔德尔·艾哈迈德：撰写，验证，形式分析。萨阿德·阿里·阿尔谢赫里：调查，监督，形式分析，资源。

通讯作者

通信地址为 卡马尔·Y·塔朱德恩.

利益冲突

作者声明没有利益冲突。

出版者按

施普林格·自然对于出版地图和机构隶属关系中的管辖权主张保持中立。

开放存取本文根据知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议发布，该协议允许任何非商业用途、分享、分发和复制任何形式的作品，只要您对原作者及来源给予适当的署名，并提供指向知识共享许可协议的链接，在修改材料的情况下指明您是否对其进行了改动。在未经本许可下，您无权分享由此文章或其部分内容衍生出来的改编作品。除非文中另外注明了版权归属条款，本文中的图片或其他第三方材料均包括在此文章的知识共享许可协议中。如果有关材料未包含在该文章的知识共享许可协议内，并且您的预期用途不被相关法律法规允许或者超出授权范围，则您需要直接向版权所有者获取许可。欲查阅本许可证的副本，请访问http://creativecommons.org/licenses/by-nc-nd/4.0/.

重印和许可