
数学家利用人工智能发现流体方程中隐藏的问题广达杂志
作者:By Charlie Wood January 9, 2026
大约 200 年前,物理学家克劳德-路易斯·纳维尔和乔治·加布里埃尔·斯托克斯完成了一组描述流体如何旋转的方程。近 200 年来,纳维-斯托克斯方程一直是现实世界中流体行为的无可挑剔的理论——从大陆之间穿行的洋流到包裹着飞机机翼的空气。
然而,许多数学家怀疑方程深处隐藏着故障。他们有预感,在某些情况下,该理论会失败。在这些情况下,方程将预测流体以某种非物理的、难以理解的方式移动——例如,旋转成速度极快的漩涡,或者立即逆转其流动。正如数学家所说,方程中的某些量会变得无限大,或者“爆炸”。
尽管付出了巨大的努力,但没有人能够提出纳维-斯托克斯方程失效的情况。这样做——或者证明方程永远不会崩溃——将获得 100 万美元的奖励。因此,作为解决纳维-斯托克斯问题的前奏,数学家们在各种简化的流体方程中寻找爆炸(也称为奇点),例如仅在一维中运行的方程。
他们找到了。但基本上他们发现的所有奇点都是“稳定的”,这意味着它们可以通过多种可能的方式形成。在包括纳维-斯托克斯在内的最现实的流体理论中,爆炸(如果存在的话)可能要微妙得多,以难以想象的精确方式发生。这些“不稳定”的爆发几乎是不可能找到的,就像大海捞针一样。
在这些现实的理论中,“很多人相信存在奇点,但它们是不稳定的,所以我们永远看不到它们,”说查理·费弗曼是普林斯顿大学的数学家,他提出了价值百万美元的纳维-斯托克斯挑战。
现在,一组数学家已经开发出一种训练机器来发现这些幽灵故障的方法。在 9 月份发布的预印本中,他们重新检查了已知存在稳定奇点的更简单的流体方程。在那里,他们发现了额外的潜在的爆炸情景– 包括不稳定的。这是第一次在多维流体中发现可能不稳定的奇点。
该团队还在其他几个流体方程中发现了各种不稳定奇点候选者。他们还没有发现任何价值百万美元的奇点。他们还需要严格证明他们发现的那些确实会爆炸。但他们成功地发现了简单模型中潜在的不稳定奇点,这让人们燃起了希望,即在更高风险的场景中也有可能发现不稳定的爆炸。
“不稳定奇点的想法不再阻碍奇点的发现,”费弗曼说,他没有参与这项新研究。
奇点狩猎
纳维-斯托克斯方程的解捕捉到了永恒的一部分。求解流体的某些初始状态的方程将告诉您流体在空间中每个点和时间上每个时刻的速度。在一个简单的解决方案中,流体可能会开始平静并永远保持平静。在更复杂的设置中,温和的水流可能会合并成漩涡和漩涡。最大的谜团是,每一个解——满足纳维-斯托克斯方程的每一个可能的流体历史——是否在任何地方、任何时候都有意义。
但解决三维流体的纳维-斯托克斯方程是难以言喻的困难,因此数学家们开始研究该问题的更简单的版本。例如,欧拉方程假设流体流动时没有内摩擦或粘度。能量不会在这些无摩擦流体中消散,因此它们应该比粘性流体更容易爆炸。
但即使在这种更简单的情况下,找到爆炸解决方案也很困难。流体方程通常太复杂,无法直接用铅笔和纸求解。因此,一种常见的方法是使用计算机模拟流体的运动,并大致了解似乎会产生爆炸的条件。如果您能够精确地识别爆炸产生的条件,您也许能够利用这些知识来严格证明爆炸确实存在。
这就是方法托马斯·侯和郭罗拍摄于 2013 年,当时他们模拟了罐中的数字液体。他们将液体的上半部分设置为一个方向旋转,下半部分设置为另一个方向,然后使用欧拉方程随着时间的推移演变这种情况。最终,在相反的流体沿着罐边界相遇的点处,涡度(衡量液体围绕某一点旋转多少的量度)变得很大——超出了计算机的处理能力。
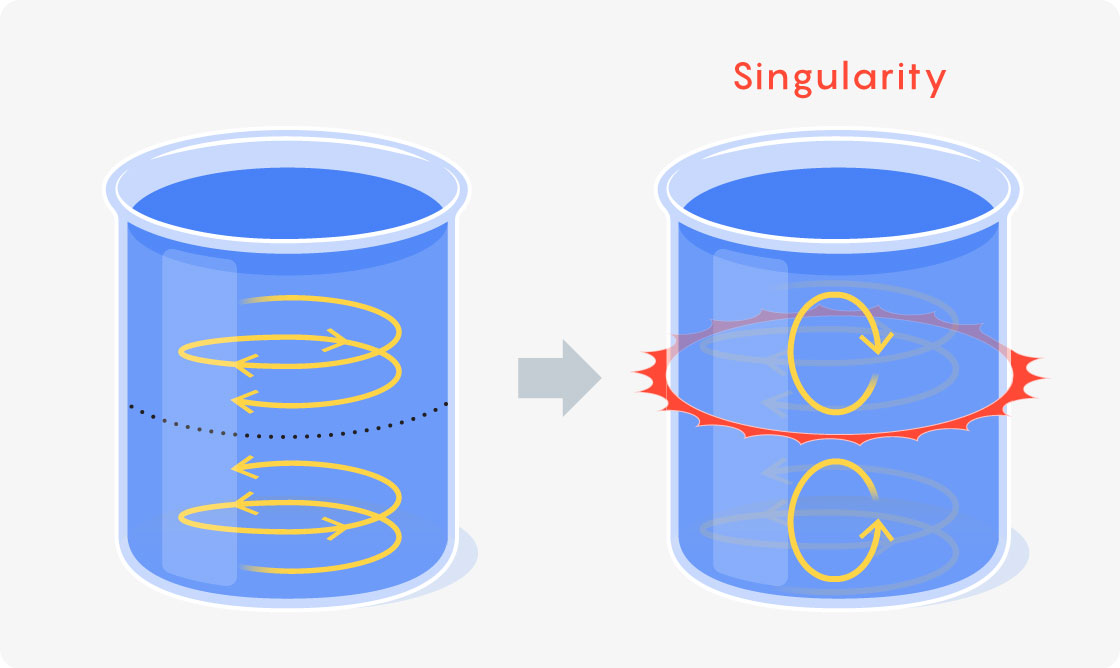
马克·贝兰/广达杂志
这暗示着类似的条件会导致爆炸。但这并不能保证。“墓地里到处都是所谓的 3D 欧拉奇异解,”费弗曼说。
侯和另一位合作者,陈家杰,用了近十年的时间才消除了“所谓的”。2022年,他们用计算机证明了奇点候选者暗示了真实奇点的存在。这是一个具有里程碑意义的证明,它让数学家们渴望进一步推动前沿。
该研究依赖于计算机模拟,这意味着对数字流体初始状态(或任何数字舍入误差)的微小调整不会影响流体的命运。即使事情的发展略有不同,奇点仍然会出现在罐边界处。
因此,奇点是稳定的。但奇点不一定是稳定的。只有当流体以最微妙的方式形成时,才可能发生爆炸。在这种情况下,对初始布置的任何调整,无论多小,都会防止流体喷出。
许多数学家推测,如果奇点确实潜伏在更现实的流体方程中,它们就会像这样不稳定,毫无征兆地突然出现。
它们也将更难找到。
走向有限
通过计算机模拟来追踪不稳定奇点候选者基本上是不可能的。首先,你需要运气好才能为你的液体找到完全正确的初始配置——类似于试图在笔尖上完美平衡一支钢笔,说特里斯坦·巴克马斯特,纽约大学数学家。然后,为了保持平衡,你还必须让流体从一个时刻到下一个时刻完美地演化,因为即使是最小的偏差也会使它走上一条不会爆炸的路径。
计算机无法达到无限的精度。它们将不可避免地引入数值误差,尽管这些误差很小,但会阻止不稳定奇点的形成。“就像风吹过你的笔一样,”巴克马斯特说。
